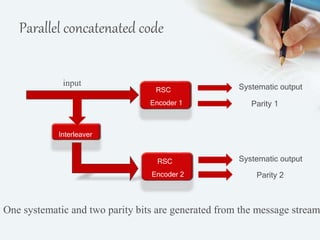
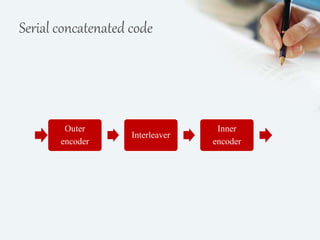
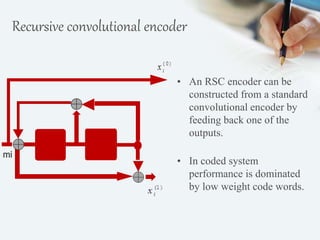
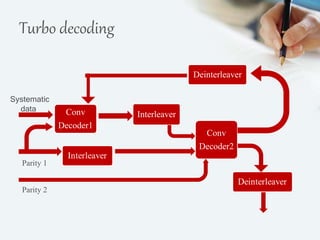
The document discusses turbo codes, a type of forward error correction code. Turbo codes use parallel concatenated convolutional encoders with pseudorandom interleaving and iterative decoding. This structure allows turbo codes to achieve error correction performance very close to the theoretical limit defined by the Shannon capacity. Some key advantages of turbo codes are their remarkable power efficiency and ability to support delivery of multimedia services through design tradeoffs. However, turbo codes also have long latency and poor performance at very low bit error rates.