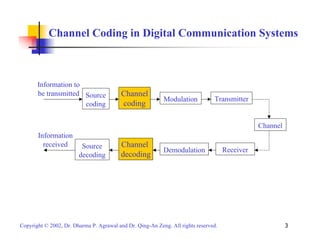
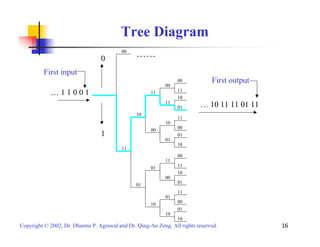
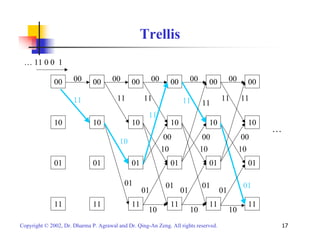
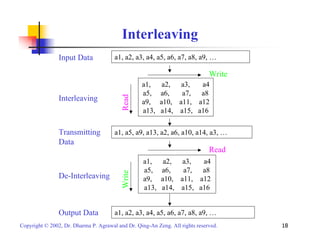
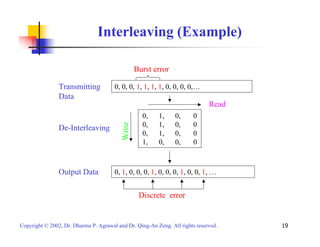
This document provides an overview of various channel coding techniques used in digital communication systems to combat noise and errors during transmission. It describes forward error correction methods like block codes, cyclic codes, convolutional codes and turbo codes. It also discusses error detection techniques like cyclic redundancy checks. Finally, it covers automatic repeat request protocols for retransmitting corrupted data packets.




![Block Codes: Linear Block Codes
ƒ Linear Block Code
The block length c(x) or C of the Linear Block Code is
c(x) = m(x) g(x) or C = m G
where m(x) or m is the information codeword block length,
g(x) is the generator polynomial, G is the generator matrix.
G = [p | I],
where pi = Remainder of [xn-k+i-1/g(x)] for i=1, 2, .., k, and I
is unit matrix.
ƒ The parity check matrix
H = [pT | I ], where pT is the transpose of the matrix p.
Copyright © 2002, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 6](https://image.slidesharecdn.com/coding-140920040807-phpapp01/85/Coding-6-320.jpg)

![Block Codes: Example
Example : Find linear block code encoder G if code generator
polynomial g(x)=1+x+x3 for a (7, 4) code.
We have n = Total number of bits = 7, k = Number of information bits = 4,
r = Number of parity bits = n - k = 3.
10 L
0
01 0
p
1
L
p
[ ] ,
LLLL
0 0 1
| 2
G P I
= =
L
k p
∴
where
L =
i k
n k i
Re
1
=
− + −
i , 1, 2, ,
g x
p mainder of x
( )
Copyright © 2002, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 8](https://image.slidesharecdn.com/coding-140920040807-phpapp01/85/Coding-8-320.jpg)
![Block Codes: Example (Continued)
1 [110]
3
+ +
p x
= x
1 Re 3
= + →
1
x x
[011]
4
+ +
p x
Re 2
= x x
2 → + =
1
3
x x
1 [111]
5
+ +
p x
Re 2
= x x
3 → + + =
1
3
x x
1 [101]
6
+ +
p x
Re 2
= x
4 → + =
1
3
x x
1101000
=
1010001
0110100
1110010
G
Copyright © 2002, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 9](https://image.slidesharecdn.com/coding-140920040807-phpapp01/85/Coding-9-320.jpg)







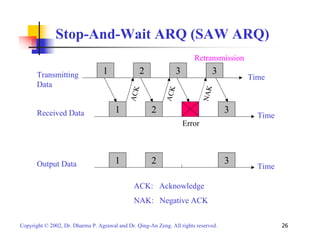
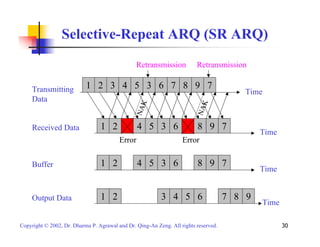
![Stop-And-Wait ARQ (SAW ARQ)
Throughput:
S = (1/T) * (k/n) = [(1- Pb)n / (1 + D * Rb/ n) ] * (k/n)
where T is the average transmission time in terms of a block duration
T = (1 + D * Rb/ n) * PACK + 2 * (1 + D * Rb/ n) * PACK * (1- PACK)
+ 3 * (1 + D * Rb/ n) * PACK * (1- PACK)2 + …..
= (1 + D * Rb/ n) / (1- Pb)n
where n = number of bits in a block, k = number of information bits in a block,
D = round trip delay, Rb= bit rate, Pb = BER of the channel, and PACK = (1- Pb)n
Copyright © 2002, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 27](https://image.slidesharecdn.com/coding-140920040807-phpapp01/85/Coding-27-320.jpg)
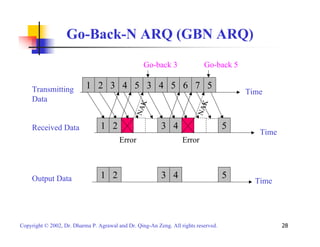
![Go-Back-N ARQ (GBN ARQ)
Throughput
S = (1/T) * (k/n)
= [(1- Pb)n / ((1- Pb)n + N * (1-(1- Pb)n ) )]* (k/n)
where
T = 1 * PACK + (N+1) * PACK * (1- PACK) +2 * (N+1) * PACK *
(1- PACK)2 + ….
= 1 + (N * [1 - (1- Pb)n ])/ (1- Pb)n
Copyright © 2002, Dr. Dharma P. Agrawal and Dr. Qing-An Zeng. All rights reserved. 29](https://image.slidesharecdn.com/coding-140920040807-phpapp01/85/Coding-29-320.jpg)