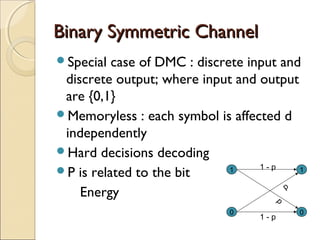
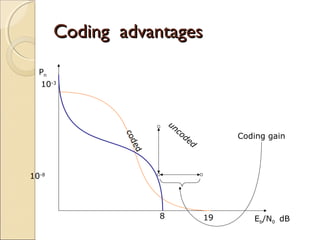
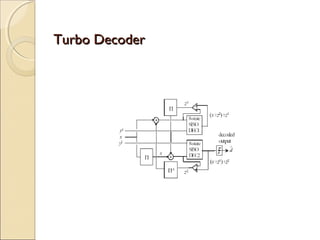
Turbo codes provide reliable communication at high data rates by combining concepts from block and convolutional codes. They use two convolutional encoders separated by an interleaver, producing redundant parity bits. During iterative decoding, probabilistic information from the first decoder is used as a priori information for the second decoder, and vice versa, improving the estimates of the transmitted bits at each iteration. Turbo codes achieve performance close to the theoretical channel capacity limit with low error rates. They have applications in deep space communications, mobile wireless systems, and other areas requiring high reliability transmission.

1. Turbo CodesTurbo Codes
SUBMITTED BY,SUBMITTED BY,
S. VASANTHA KUMARANS. VASANTHA KUMARAN
M.TECH [ECE] FIRST YEARM.TECH [ECE] FIRST YEAR
REG NO:REG NO:: 16304027: 16304027

2. AgendaAgenda
Objectives
Error Correction Codes
Turbo Codes Technology
Turbo decoding
Turbo Codes Performance
Application
Conclusion

3. ObjectivesObjectives
◦ Studying channel coding
◦ Understanding channel capacity
◦ Ways to increase data rate
◦ Provide reliable communication link

4. Error Correction CodingError Correction Coding
 Channel coding adds structured redundancy to a transmission.
◦ The input message m is composed of K symbols.
◦ The output code word x is composed of N symbols.
◦ Since N > K there is redundancy in the output.
◦ The code rate is r = K/N.
 Coding can be used to:
◦ Detect errors: ARQ
◦ Correct errors: FEC
Channel
Encoderm x

5. Error Correction CodesError Correction Codes
Block
Convolutional
Turbo code
◦ Technically a block code
◦ Works like both Block and Convolutional
codes

6. Block CodeBlock Code
Most common is Hamming Code
Take a block of length, k (information
sequence)
Then encode them into a codeword, the
last (n-k) bits are called parity bits
Parity bits used for error checking and
correcting

7. Convolutional CodesConvolutional Codes
Continuous or Streaming coding
Viterbi and Soft Output Viterbi are the
most common

8. Turbo CodesTurbo Codes
Mix between Convolutional and Block
codes
Require a Block code
HOWEVER, they use shift registers like
Convolutional Codes

9. Turbo Codes HistoryTurbo Codes History
IEEE International Comm conf 1993 in
Geneva
Berrou, Glavieux. : ‘Near Shannon Limit
Error-Correcting Coding : Turbo codes’
Provided virtually error free
communication at data date/power
efficiencies beyond most expert though

10. The Turbo-PrincipleThe Turbo-Principle
Turbo codes get their name because the
decoder uses feedback, like a turbo
engine.

11. Communication SystemCommunication System
Structural modular approach
Channel
Coding
Source
Coding
Modulation
Formatting
Digitization
Multiplexing
Access
techniques
send
receive

12. Channel CodingChannel Coding
Accounting for the channel
Can be categorized into
◦ Wave form signal design
 Better detectible signals.
◦ Structured sequences
 Added redundancy
Objective: provide coded signals with
better distance properties

13. Binary Symmetric ChannelBinary Symmetric Channel
Special case of DMC : discrete input and
discrete output; where input and output
are {0,1}
Memoryless : each symbol is affected d
independently
Hard decisions decoding
P is related to the bit
Energy
1
00
11 - p
1 - p
p
p

14. Gaussian ChannelGaussian Channel
 descrete inputs with continuous property
Noise get added to the signals passing
through it
Noise is a Gaussian random variable with
zero mean and variance σ2
The resulting pdf is
2
2
2
)(
2
1
)|( σ
πσ
kuz
k euzp
−−
=
Likelihood of uk

15. Why use ECCWhy use ECC
Consider the following trade offs
◦ Error performance vs. bandwidth
 High redendency consumes bw
◦ Power vs. bandwidth
 Reduction in Eb/N0
◦ Data rate vs. bandwidth
 Higher rate

16. Error Correction MechanismsError Correction Mechanisms
Backward Error correction
◦ Error detection capability
◦ Communication cost
◦ Real time traffic
Forward Error Correction
◦ Detection and correction of errors
◦ More complex receivers
◦ DSP cost

17. Forward Error CorrectionForward Error Correction
Block Codes
◦ Data split into blocks
◦ Checks are within the block
Convolutional code
◦ Bit streamed data
◦ Involves memory
Turbo codes
◦ Uses conv. Codes
◦ Special properties

18. Coding advantagesCoding advantages
Pn
Eb/N0 dB
uncoded
coded
10-8
10-3
8 19
Coding gain

19. Coding disadvantagesCoding disadvantages
More bandwidth due to redundant
Processing Delay
Design Complexity

20. Turbo codesTurbo codes
Parallel concatenated
◦ The k-bit block is encoded N times with
different versions (order)
◦ Pro the sequence remains RTZ is 1/2Nv
◦ Randomness with 2 encoders; error pro of
10-5
◦ Permutations are to fix dmin

21. Turbo EncoderTurbo Encoder
Input
RSC
RSC
Interleaver
Systematic codeword
random
X
Y1
Y2

22. Turbo EncoderTurbo Encoder
The output stream of data consists of the
systematic data, parity bits from
encoder1, and parity bits from encoder2
Through the use of the interleaver, the
decoder will have two independent looks
at the same data, and can use both
streams to decode the information
sequence

23. Turbo DecodingTurbo Decoding
Criterion
◦ For n probabilistic processors working
together to estimate common symbols, all of
them should agree on the symbols with the
probabilities as a single decoder could do

24. Turbo DecodingTurbo Decoding
Two decoders used in serial fashion, with
output of one decoder used as prior
information to next decoder
Feedback in decoding circuit allows for multiple
iterations, and improves bit error performance
D1 D2I
Inv(I)
Parity2
Parity1
Le12 Le21
Systematic

25. Turbo DecoderTurbo Decoder

26. Turbo DecoderTurbo Decoder
• The inputs to the decoders are the Log
likelihood ratio (LLR) for the individual symbol
d.
• LLR value for the symbol d is defined ( Berrou)
as

27. Steps in Turbo DecodingSteps in Turbo Decoding
Evaluate the path metrics
Trace back to obtain the decisions (x)
Trace back using alternate paths to obtain the
metric differences
Compute the minimum of all possible metric
differences for that stage
Obtain the reliability of decision
Pass this reliability of decision to next decoder
Iterate the above steps

28. Turbo Codes PerformanceTurbo Codes Performance

29. Turbo Codes ApplicationsTurbo Codes Applications
Deep space exploration
◦ France SMART-1 probe
JPL equipped Pathfinder 1997
Mobile 3G systems
◦ In use in Japan
◦ UMTS
◦ NTT DoCoMo
 Turbo codes : pictures/video/mail
 Convolutional codes : voice

30. ConclusionConclusion
Turbo codes achieved the theorical limits
with small gap
Give rise to new codes : Low Density
Parity Check (LDPC)
Needs
◦ Improvements in decoding delay