This document describes the Hamming code system. It introduces Hamming codes, which can detect up to two-bit errors or correct one-bit errors. It discusses different types of errors, the Hamming bound condition, and how to implement Hamming codes by calculating parity bits using a generator matrix and decoding received codewords using a parity check matrix to detect and correct errors through syndrome decoding. The document also includes a MATLAB source code example to simulate the encoding, transmission over an AWGN channel, and decoding of Hamming codes to calculate the bit error rate.

1. Hamming Code System
Name- Dilshad Ahmad
Roll No-MT/EC/10007/19
Subject Code-EC564
Name- Richa Anand
Roll No-MT/EC/10014/19
Subject Code-EC564
ECE Dept. , BIT Mesra, Ranchi, 835215
5/30/2020
1

2. Content
 Introduction
 Errors
 Type of Errors
 Hamming Bound
 Hamming Code system
 Implementation of Hamming Code
 Syndrome and Decoding
 MATLAB Implementation Flow chart
 Source Code
 Output
 Conclusion
5/30/2020
2

3. Introduction
 Data can be corrupted during transmission, For reliable communication, errors must be
detected and corrected
 So we required a ‘Coding technique’ to overcome these errors at receiver.
 There is always some Bit Error Rate so to maintain some QoS we do encoding and
Decoding with a particular coding Scheme
 So There are Various coding scheme used according to need and Application, like
Hamming code, cyclic coding convolutional code etc.
5/30/2020
3

4. Errors
 What is Error?
o Error is a condition when the output information does not match with the input information. During
transmission, digital signals suffer from noise that can introduce errors in the binary bits travelling
from one system to other.
o That means a 0 bit may change to 1 or a 1 bit may change to 0.
 Error Detection: Error detection is the detection of errors caused by noise or other
impairments during transmission from the transmitter to the receiver.
 Error correction: Error correction is the detection of errors and reconstruction of the original,
error-free data.
5/30/2020
4

5. Type of Error:
 There are Mainly Three Types of Errors Occurs
1. Single bit error.
2. Multi bits error.
3. Burst bits error.
1 0 1 0 1 0 1 1 1 0 1 0
Single bit error: In a frame, there is only one bit, anywhere though, which is corrupt
1 0 1 0 1 0 0 1 1 0 1 0
Multi bit error: Frame is received with more than one bits in corrupted state.
1 0 1 0 1 0 0 1 1 1 1 1
Burst bit error: Frame contains more than1 consecutive bits corrupted..
5/30/2020
5

6. Hamming code:
 Around 1947 Richard W. Hamming developed technique for detecting and correcting single bit
errors in transmitted data. His technique requires that three parity bits (or check bits) be
transmitted with every four data bits. The algorithm is called a (7, 4) code, because it requires seven
bits to encoded four bits of data.
 In communication, Hamming codes are a family of linear error-correcting. Hamming codes can
detect up to two-bit or correct one-bit errors without detection of uncorrected errors.
0 0 1 1 0 1 0 1 1 1 1 0 1 0
0 0 1 1 0 1 0
1 1 1 1 0 1 0
Detection
Hamming Decoding
At Receiver
2 bit Detected
At Transmitter
1 0 1 1 0 1 0
Channel
At Receiver
1 bit Error Corrected
 Now Lets See what is these Hamming codes…
5/30/2020
6

7. Hamming Bound
 Any ( n, k ) code which is capable of correcting ‘t’ errors should satisfy the following condition
Called Hamming Bound
2 𝑛−𝑘 ≥ 𝑖=0
𝑡
𝑛𝐶𝑖 For t=1(Single Error Correcting code)
2 𝑛−𝑘 ≥n+1
 Any code which satisfy the equality condition in the hamming bound called perfect code
 For n=7, k=4 Equality condition hold
 So (7,4 ) single error correcting perfect code is called Hamming code
5/30/2020
7

8. Implementation of Hamming Code
 To implement Hamming code firstly we calculate Parity Bits
 Generator Matrix- It is matrix of [I,P] use to encode message bits
 For Example
 p1 = d2 + d3 + d4
p2 = d1 + d3 + d4
p3 = d1 + d2 + d4
5/30/2020
8

9. Continued…
 So for any Message bits (4 bits) we can get code directly using Generator matrix
C=[d]*[G]
 We send this Codeword through Channel and at receiver we decode this codeword
using parity check matrix also we find error is there or not
 Let at Receiver we get a received codeword “r”
5/30/2020
9

10. Syndrome and Decoding
 Syndrome-The pattern of errors, called the error syndrome, identifies the bit in error.
 If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the
erroneous parity bits identifies the erroneous bit.
S=[r]. [HT]
If S =0 No Errors
S ≠ 0 Errors are there and we got Error Vector e
 S also gives location of error and this location vector verified from [HT]
5/30/2020
10

11. Continued…
 At last after getting the error vector e
Correct codeword= r + e
 This Syndrome Decoding for Hamming Code and error vector can’t correct more than
one error vector
 For correction more errors we have to add more redundancy
5/30/2020
11

12. MATLAB Implementation
 Flow Chart
Transmitter Receiver side
Channel
Start
Generator
Matrix
creation
Encoding
Parity
Generation
AWGN
Channel
Decoding
BER
Calculation
Error
Calculations
Stop 5/30/2020
12

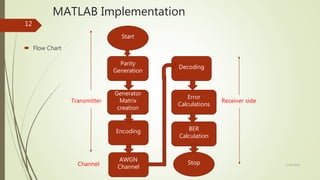
13. Source Code
EbN0dB=2; Energy Per Bit
R=4/7; % (7,4) Hamming code Rate
EbN0=10^(EbN0dB/10); % Anti Log
sigma=sqrt(1/2*R*EbN0);
k=4; n=7;
Nerrs=0; Nblocks=1000; % 1000 blocks
for i = 1:Nblocks
msg=randi([0,1],1,k); %Random Msg Generation
%Encoding
cword=[msg mod(msg(1)+msg(2)+msg(3),2)...
mod(msg(2)+msg(3)+msg(4),2)...
mod(msg(1)+msg(2)+msg(4),2)];
s=1-2*cword;% BPSK bit to symbol conversion
r= s+sigma*randn(1,n); % AWGN CHANNEL
% Hard Decoding
b=(r<0); % Thresholg at Zero
dist= mod(repmat(b,16,1)+cwords,2)*ones(7,1);
[mind1,pos]=min(dist);
msg_cap1=cwords(pos,1:4);
%Soft Decoding
corr=(1-2*cwords).*r;
[mind2,pos]=max(corr);
msg_cap2=cwords(pos,1:4); % Decoded msg
Nerrs=Nerrs+sum(msg~=msg_cap1); % Eroors Calculation
end
BER_sim=Nerrs/k/Nblocks; % BER Calculation
% Name:
disp([EbN0dB BER_sim Nerrs k*Nblocks]);
5/30/2020
13

14. Output
For EbN0dB=2 ;
disp([EbN0dB R BER_sim Nerrs k*Nblocks]);
2 0.57143 0.05505 2202 40000
msg = % Random Input msg
0 0 0 1
cword =
0 0 0 1 0 1 1
%After AWGN Channel Received Code
r =
1.9644 0.455 1.1051 -1.89 1.2222
-0.62404 2.2142
msg_cap1 =% Decoded Msg
0 0 0 1
For EbN0dB=4 ;
disp([EbN0dB R BER_sim Nerrs k*Nblocks]);
4 0.57143 0.01545 618 40000
msg = % Random Input msg
0 1 0 0
cword =
0 1 0 0 1 1 1
%After AWGN Channel Received Code
r = 1.4018 -0.29702 0.51536 0.94538 -1.5975 -1.9073
0.36304
msg_cap1 =
0 1 0 0
5/30/2020
14

15. Conclusion
 Hamming Code system is very much important where we need only one
error correction and two error detection system, it is very easy to
implement and for large number of block of bits it is more efficient.
5/30/2020
15

16. 5/30/2020
16