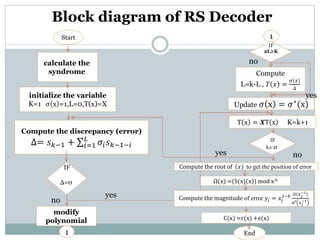
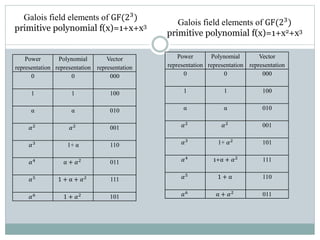
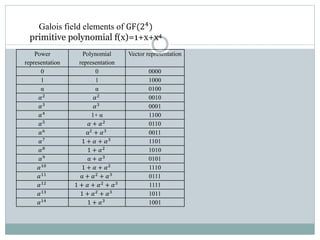
The document outlines Reed-Solomon error correction codes. It discusses how Reed-Solomon codes encode data using a generator polynomial to produce parity check symbols. The document then describes how Reed-Solomon codes can decode errors using syndrome calculation, error location polynomials, and finding the error positions and values through algorithms like Forney's method and Chien search. Reed-Solomon codes are widely used in applications like CDs, DVDs, wireless communications and digital television for their ability to efficiently correct both random and burst errors.

1. Ameer Hussein Mohammed
Reed Solomon

2. OUTLINES
Reed-Solomon code
Encoding of RS Codes
Decoding of RS Codes
Reed Solomon vs BCH
References

3. Reed-Solomon
RS codes
BCH codes
Cyclic codes
Linear block codes
Reed-Solomon (RS) codes is a special class of non-binary BCH codes

4. • Discovered by Irving Reed and Gustave Solomon in
1960.
• RS codes are very powerful in correcting both random
errors and bursty errors.
• In RS system, the decoder corrects a symbol, it
replaces the incorrect symbol with a correct one,
whether the error was caused by one bit being
corrupted or all symbol bits being corrupted, this
gives the RS code an advantage over binary codes.
Introduction

5. • today RS code are found in numerous consumer
products, such as
• mass storage devices (e.g., CDs and DVDs)
• broadband modems (e.g., cable modems)
• wireless mobile communications systems (e.g., WiMax,
cellular telephone and microwave links ).
• Digital television and DVB
Applications

6. Where :
Reed Solomon coding operates on a finite field called Galios Field GF(2m).
M is the number of a symbol
the total no. of code symbols (Code Length): n = 2𝑚-1
The No. of data symbols: k = 2𝑚
-1-2t
No. of parity check symbols: n-k = 2t
The number of error that need to correct: t
Description of RS Codes

7. Example 6
A given Reed-Solomon code with RS(204,188) of first generation
DVB standards. Find error correction capability (t).
Solution: Each code word contains 204 code word bytes, of which 188
bytes are data and 16 bytes are parity. For this code:
n = 204, k = 188
2t = n-k = 16, t = 8
The decoder can correct any 8 symbol errors in the code word: i.e.
errors in up to 8 bytes anywhere in the code word can be automatically
corrected.

8. Encoding of RS Codes
Code Generator Polynomial
An (n, k) Reed-Solomon code is constructed by forming
the code generator polynomial g(x), the roots of which are
consecutive elements of the Galois field.
Thus the code generator polynomial takes the form:
𝒈 𝒙 = 𝒙 + 𝜶 𝒙 + 𝜶𝟐
𝒙 + 𝜶𝟑
… … 𝒙 + 𝜶𝟐𝒕
Or: 𝒈 𝒙 = 𝒙 − 𝜶 𝒙 − 𝜶𝟐
𝒙 − 𝜶𝟑
… … 𝒙

9. Encoding of RS Codes
 The codeword vector for RS code can be obtained by
𝒄 𝒙 = 𝒙𝐧−𝒌
𝐦 𝒙 𝐦𝐨𝐝 𝐠(𝐱) + 𝒙𝒏−𝒌
𝒎 𝒙
Length of c(x) is n symbol
Length of m(x) is k symbol
𝑥𝑛−𝑘
𝑚 𝑥 : data shifted by n-k

10. Example 7
Consider the ( 7 , 3 ) double-symbol error correcting R-S code,
describe the generator polynomial of it.
Primitive polynomial 1 + x + x3
Ans. :
RS(n,k)=RS(7,3), n = 2𝑚
-1 : m=3
2t = n – k = 4 roots
g(x) = ( x – α ) ( x – α2 ) ( x – α3 ) ( x – α4 )
= ( x2 – (α + α2 ) x + α3 ) ( x2 – (α3 + α4 ) x + α7 )
= ( x2 – α4 x + α3 ) ( x2 – α6 x + α0 )
= x4 – (α4 + α6) x3 + (α3 + α10 + α0) x2 – (α4 + α9 ) x + α3
= x4 – α3 x3 + α0 x2 – α1 x + α3
Following the format of low order to high order, and changing negative
signs to positive, since in the binary field +1 = - 1 , the generator
polynomial becomes :
g(x) = α3 + α1 x + α0 x2 + α3 x3 + x4

11. Example 8
Consider the double error correcting RS code of block length n=15
over GF(16) describe the generator polynomial
Primitive polynomial 1 + x + x4
Sol:
When GF(16) :M=4, t=2
Primitive polynomial : 𝑓 𝑥 = 𝑥4 + 𝑥 + 1
The generator polynomial can written as:
g(x) = ( x – α ) ( x – α2 ) ( x – α3 ) ( x – α4 )
g(x)= ( x2 – (α + α2 ) x + α3 ) ( x2 – (α3 + α4 ) x + α7 )
g(x)= ( x2 – (α5 ) x + α3 ) ( x2 – (α7 ) x + α7 )
.
.
g(x)= x4 + α13 x3 + α6 x2 + α3 x+ α10

12. Consider the RS (7,3) double-symbol correcting ( 𝑡 = 2 ) Reed
Solomon Code with generator polynomial
𝑔 𝑥 = 𝛼3
+ 𝛼𝑥 + 𝑥2
+ 𝛼3
𝑥3
+ 𝑥4
. If the input sequence 𝑚(𝑥) = 𝑥,
find the systematic output codeword polynomial.
Primitive polynomial 1 + x + x3
Solution:
𝑐 𝑥 = 𝑥𝑛−𝑘𝑚 𝑥 𝑚𝑜𝑑𝑔 𝑥 + 𝑥𝑛−𝑘𝑚 𝑥
𝑥𝑛−𝑘𝑚 𝑥 = 𝑥4. 𝑥 = 𝑥5
𝑥5𝑚𝑜𝑑𝑔 𝑥 = 𝛼2𝑥3 + 𝑥2 + 𝛼6𝑥 + 𝛼6
𝒄 𝒙 = 𝒙𝟓 + 𝜶𝟐𝒙𝟑 + 𝒙𝟐 + 𝜶𝟔𝒙 + 𝜶𝟔
Example 9

13. output
D
m(x)
D
D
(n-k) shift register stages
+
+
+
α3
α1 α0 α3
+
control
D
RS Encoder circuit

14. Decoding block diagram of RS Codes
calculate the
syndrome
From the error
location
polynomial 𝝈 𝑿
calculate the
error values
Forney method
Chien search of
error positions
Data delay
Input r
output

15. The Massey FSR Synthesis Algorithm
1- Compute syndrome values:𝑺𝒌−𝟏 , 𝟏 ≤ 𝒌 ≤ 𝟐𝒕 − 𝟏
2- Initialize algorithm variables:𝝈 𝑿 = 𝟏 , 𝑳 = 𝟎 𝒂𝒏𝒅 𝑻 𝑿 = 𝑿 , 𝒌 = 𝟏
3- Take in new syndrome value and compute Discrepancy (error) “∆”
∆= 𝑺𝒌−𝟏 +
𝒊=𝟏
𝑳
𝝈𝒊𝑺𝒌−𝟏−𝒊
4- Test Discrepancy: If ∆ = 0, go to step9, otherwise, go to step5.
5- Modify connection polynomial:𝝈∗ 𝑿 = 𝝈 𝑿 + ∆. 𝑻(𝑿)
6- Test register length: if 𝟐𝑳 ≥ 𝑲, go to step8, otherwise, go to step7.

16. The Massey FSR Synthesis Algorithm
7- Changes register length and update correction term 𝑳
= 𝑲– 𝑳 𝒂𝒏𝒅 𝑻(𝒙) = 𝝈(𝑿)/∆
8- Update connection polynomial:𝝈 𝑿 = 𝝈∗(𝑿)
9- Update correction term: 𝑻 𝑿 = 𝑿. 𝑻(𝑿)
10- Update syndrome counter:𝑲 = 𝑲 + 𝟏
11- Test syndrome counter: if 𝑲 < 𝟐𝒕 + 𝟏, go to step3 otherwise,
stop.

17. Start
calculate the
syndrome
initialize the variable
K=1 𝜎 x =1,L=0,T(x)=X
Compute the discrepancy (error)
∆= 𝑠𝑘−1 + 𝑖=1
𝐿
𝜎𝑖𝑠𝑘−1−𝑖
IF
∆=0
modify
polynomial
no
1
1
IF
2L≥K
Compute
L=k-L , 𝑇 𝑥 =
𝜎 𝑥
∆
Update 𝜎 x = 𝜎∗(x)
yes
T x = 𝑿T x K=k+1
IF
k≤ 2t
yes no
no
yes
Block diagram of RS Decoder
Compute the root of 𝑥 to get the position of error
Ω(x) =(S(x) x ) mod x2t
Compute the magnitude of error 𝑦𝑗 = 𝑥𝑗
1−𝑏 𝛺(𝑥𝑗
−1
)
σ′ 𝑥𝑗
−1
End
C(x) =r(x) +e(x)

18. Forney's Equation for the Error Magnitude
𝑆 𝑋 = 𝑆𝑏+2𝑡−1𝑋2𝑡−1 + ⋯ + 𝑆𝑏+1𝑋 + 𝑆𝑏
𝑆𝑖= 𝑟(𝛼𝑖
𝑆𝑖 = 𝑟𝑛−1 𝛼𝑖 𝑛−1
+ 𝑟𝑛−2 𝛼𝑖 𝑛−2
+ ⋯ + 𝑟1 𝛼𝑖 + 𝑟0
The key equation can then be written as:
𝛺 𝑋 = 𝑆 𝑋 𝜎 𝑋 𝑚𝑜𝑑𝑋2𝑡
According to Forney's algorithm, the error value is given by:
𝑌
𝑗 = 𝑋𝑗
1−𝑏
𝛺(𝑋𝑗
−1
)
𝜎′(𝑋𝑗
−1
)
Where 𝜎′(𝑋𝑗
−1
) is the derivative of𝜎(𝑋) for 𝑋 = 𝑋𝑗
−1
When b=1,
the 𝑋𝑗
1−𝑏
term disappears, the value of b is defined in Equation C.

19. Example 10
for RS code (7,3) over GF(8). Decode the receive signal
r=(000 000 011 000 111 000 000)
primitive polynomial f(x)=1+x2+x3
Sol. according the received vector converted to polynomial
form
r(x)= α6x2+ α4x4
calculate the syndrome :
si=r(α i)
s0=r(α0)= 1
s1=r(α 1)=0
s2=r(α 2)= α 6
s3=r(α 3)= α 4

20. K=1
initialize the algorithm variable K=1 𝜎 x =1,L=0,T(x)=X
Compute the discrepancy (error) ∆:
∆= 𝑠𝑘−1 +
𝑖=1
𝐿
𝜎𝑖𝑠𝑘−1−𝑖
∆=s0 =1
𝜎∗
x = 𝜎 x + ∆. T(x) =1+1x = 1+x
when 2L<K so set L=k-L =1 T 𝑥 =
𝜎 x
∆
=
1
1
= 1
𝜎 x = 𝜎∗
x =1+x
𝑇 𝑋 = 𝑋. 𝑇 𝑋 = 𝑋 .1 = 𝑋
Increment K→2 ≤ 2t=4 , so continue

21. K=2
𝑇 𝑥 = 𝑋 L=1 𝜎 𝑥 = 1 + 𝑥
∆= 𝑠𝑘−1 + 𝑖=1
𝐿
𝜎𝑖𝑠𝑘−1−𝑖
∆=𝑠1 + 𝜎1𝑠0 =0+1×1=1
𝜎∗ 𝑥 = 𝜎 𝑥 + ∆. 𝑇 𝑥 =1 + 𝑥+x=1
2L=K skip some step, then:
𝜎 𝑥 = 𝜎∗ x =1
𝑇 𝑥 = 𝑥𝑇 𝑥 = 𝑥
2
Increment K→3 ≤ 2t=4 , so continue

22. K=3
T x = x
2
L=1 σ x = 1
∆= s2 + σ1s1=α
6
+0×0 =α
6
σ∗ x = σ x + ∆. T(x) =1+α
6
x
2
2L<k L=K-L= 3-1=2 T x =
σ x
∆
=
1
α
6 = α
σ∗(x) = σ x =1+α
6
x
2
T x = xT x =α x
Increment K→4 ≤ 2t , so continue

23. K=4
𝑇 𝑥 = 𝛼𝑥 L=2 σ x = 1 + 𝛼
6
𝑥
2
∆=𝑠3 + 𝜎1𝑠2 +𝜎2 𝑠1 = 𝛼
4
+0×𝛼
6
+𝛼
6
×0 =𝛼
4
σ∗ x = σ x + ∆. 𝑇(𝑥)
= 1 + 𝛼
6
𝑥
2
+𝛼
4
. 𝛼𝑥 = 1 + 𝛼
5
𝑥+𝛼
6
𝑥
2
2L=K skip some step, then:
σ x = σ∗
x = 1 + 𝛼
5
𝑥+𝛼
6
𝑥
2
𝑇 𝑥 = 𝑥𝑇 𝑥 =𝛼𝑥
2
The process is complete
σ x = 1 + 𝛼
5
𝑥+𝛼
6
𝑥
2
S(x)=s0+s1x+s2x2+s3x3 =1 +𝛼
6
𝑥
2
+𝛼4𝑥3

24. After the substitute the field element 𝛼
0
….. 𝛼
6
we get
The root of σ 𝑥 is 𝛼3 and 𝛼5
X1=
1
𝛼
3 =𝛼
4
X2=
1
𝛼
5 =𝛼
2
Ω(x)=(S(x)σ x )mod x2t
=(1+ α5x+ α4x4+ α3x5)mod x4
Ω(x) = 1+ α5x = rem(x)
σ x = 1 + 𝛼
5
𝑥+𝛼
6
𝑥
2
σ′
𝑥𝑗
−1
= 𝛼
5
𝑦𝑗 = 𝑥𝑗
1−𝑏
𝛺(𝑥𝑗
−1
)
σ′ 𝑥𝑗
−1

25. 𝑦𝑗 = 𝑥𝑗
1 𝛺(𝑥𝑗
−1
)
σ′ 𝑥𝑗
−1
Ω(x) = α5x+1
𝑦1 = 𝑥1
1 𝛼
5
𝑥1
−1+1
𝛼
5 = 𝛼
4 𝛼
5
𝛼
3
+1
𝛼
5 = 𝛼
4
𝑦2 = 𝑥2
1 𝛼
5
𝑥2
−1+1
𝛼
5 = 𝛼
2 𝛼
5
𝛼
5
+1
𝛼
5 = 𝛼
6
e(x)=α4x4+ α6x2
C(x)=r(x)+e(x)= α6x2+ α4x4 + α4x4+ α6x2
C(x) = 000 000 000 000 000 000 000

26. Reed-Solomon with First Generation
 The standards DVB-C, DVB-T, DVB-S are used Reed-Solomon
RS (204,188, t = 8) code .
 Due to the complexity and implementation cost of Reed Solomon
codes it is preferred to use BCH codes instead of RS in the
second generation.
 The Reed-Solomon code has codewords length 204 bytes, and
data dimension 188 bytes and allows to correct up to 8 random
erroneous bytes in a received word of 204 bytes.
 Code Generator Polynomial is:
𝑔 𝑥 = 𝑥 + 𝛼 𝑥 + 𝛼2
𝑥 + 𝛼3
… … (𝑥 + 𝛼16
)
(188 BYTES) USER
FRAME
16 PARITY
SYMBOLS
n-k=16
k=188
n=204

27. Reed Solomon vs BCH
BCH
RS
Its binary cyclic code
Its non-binary cyclic code
Minimum error correction
capability t=1 byte and
maximum
capability up to t=12 bytes
Minimum error correction
capability t=2 byte and
maximum capability up to t=8
bytes
Use in outer coding of DVB-
S2, DVB-C2, DVB-T2
Use in outer coding of DVB-S,
DVB-C, DVB-T
Outer Coding Standard depend
on Inner coding rate
Outer Coding Standard is
RS(204,188,t=8)
Easy Decoding process
Complex Decoding process

28. References
1. P. Sweeney, “Error Control Coding From Theory to Practice”, Wiley, 2002.
2. Y.Jiang, “A Practical Guide to Error-Control Coding Using MATLAB”, Artech
House, 2010.
3. S. Lin, and D.J. Costello Jr. “Error Control Coding Fundamentals and
Applications”, Prentice Hall, 1983.
4. Ulrich Reimers, “DVB The Family of International Standards for Digital Video
Broadcasting”, Second Edition, Springer-Verlag Berlin Heidelberg, 2005.
5. Jorge Castiñeira Moreira and Patrick Guy Farrell,‘ 'ESSENTIALS OF ERROR-
CONTROL CODING'', John Wiley & Sons Ltd, 2006.

29. Power
representation
Polynomial
representation
Vector
representation
0 0 000
1 1 100
α α 010
𝛼2
𝛼2
001
𝛼3
1+ α 110
𝛼4
α + 𝛼2
011
𝛼5 1 + α + 𝛼2
111
𝛼6
1 + 𝛼2
101
Galois field elements of GF(23)
primitive polynomial f(x)=1+x+x3
Power
representation
Polynomial
representation
Vector
representation
0 0 000
1 1 100
α α 010
𝛼2
𝛼2
001
𝛼3
1+ 𝛼2
101
𝛼4
1+α + 𝛼2
111
𝛼5 1 + α 110
𝛼6
α + 𝛼2
011
Galois field elements of GF(23)
primitive polynomial f(x)=1+x2+x3

30. Power
representation
Polynomial
representation
Vector representation
0 0 0000
1 1 1000
α α 0100
𝛼2
𝛼2
0010
𝛼3
𝛼3
0001
𝛼4
1+ α 1100
𝛼5 𝛼 + 𝛼2
0110
𝛼6
α2
+ 𝛼3
0011
𝛼7
1 + 𝛼 + 𝛼3
1101
𝛼8
1 + 𝛼2
1010
𝛼9
α + 𝛼3
0101
𝛼10
1 + 𝛼 + 𝛼2
1110
𝛼11
α + 𝛼2
+ 𝛼3
0111
𝛼12
1 + 𝛼 + 𝛼2
+ 𝛼3
1111
𝛼13
1 + 𝛼2
+ 𝛼3
1011
𝛼14
1 + 𝛼3
1001
Galois field elements of GF(24)
primitive polynomial f(x)=1+x+x4

31. Thank you