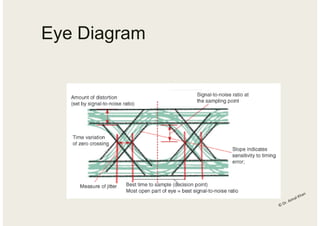
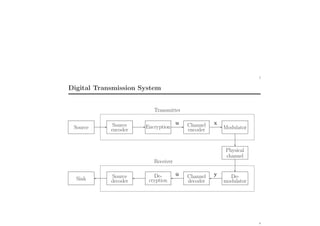
This course outline covers topics in digital communications including basic blocks, signal classification, spectral density, sampling theory, pulse code modulation, quantization, error performance, and detection techniques. Key concepts that will be discussed are bandwidth calculation, inter-symbol interference, eye diagrams, pulse shaping, equalization, channel coding, and convolutional codes.

1. Course Outline
■ Digital Communications Basic Blocks, Introduction
■ Classification of signals ,Deterministic and Random, Periodic
and Non-periodic (Signal, Energy and Power Signals, Analog
and Discrete Signals)
■ Spectral Density, Auto-Correlation,
■ Bandwidth of Digital Signals, Baseband versus Band pass
■ Sampling Theorem, Aliasing, Over Sampling
■ Sampling and Quantizing effects, Channel effects, Signal to
Noise Ratio
■ Pulse Code Modulation, PCM based Time division
multiplexing

2. Course Outline
■ Uniform and Non Uniform Quantization, Companding
■ Waveform Representation of Binary Digits, M-ary Pulse
Modulation waveforms
■ PCM waveform types, Line Coding
■ Correlative Coding, duo-binary coding and decoding, precoding
■ Error Performance, degradation in Digital Communication
System, Demodulation and detection, SNR parameter in Digital
Communication System
■ Detection of Binary Signals in Gaussian Noise, Matched Filter

3. Course Outline
■ Inter symbol Interference, Pulse shaping to reduce ISI, Error
Performance
■ Eye Patterns, Digital Demodulation Techniques
■ Spread Spectrum, Frequency Hopping and Direct Sequence

4. What we discussed in the last
lecture
■ Bandwidth Calculation
■ Inter Symbol Interference

5. Eye Diagram

6. How to combat ISI
■ Pulse shaping
By using Nyquist Pulses
■ Using Equalization
Zero Forcing Equalization
Mean Minimum Square Equalizer

7. Channel Coding in Our Everyday Lives: Examples
185

8. Channel Coding in Our Everyday Lives: Examples
186

9. Channel Coding in Our Everyday Lives: Examples
187

10. 188
What is Channel Coding?
Digital Communications over physical channels is prone to errors
Channel Coding means :
Introducing redundancy (i.e., adding extra
bits) to information messages to protect
against channel errors

11. 4
What is Channel Coding?
Channel coding is the art or science in order to protect data symbols
against transmission/storage errors. Channel coding in only possible in digital
transmission/storage systems.
Redundancy is added to the data at the transmitter side, so that
transmission/storage errors can be detected and/or corrected at the receiver.
Main tasks:
• Error detection
• Error correction
• Error concealment.
Without channel coding, robust data transmission via noisy communication channels
as well as reliable storage is not possible. Therefore, channel coding is applied in many
different applications, particularly in digital transmission systems and in digital
storage systems.

12. 5
Applications of Channel Coding
Digital transmission systems
• mobile radio systems
• data modems, internet
• satellite communication systems, deep-space probes
• underwater communication systems
• optical communication systems
Digital storage systems
• compact disc (CD), digital versatile disc (DVD), coin disc
• digital audio tape (DAT)
• hard disc, magnetic storage systems
6

13. 7
Digital Transmission System
Source E Source
encoder
E
Encryption E Channel
encoder
E
Modulator
c
Physical
channel
c
De-
modulator
'Channel
decoder
'De-
cryption
'Source
decoder
'
Sink
u
ˆu
x
y
Transmitter
Receiver
8

14. 8
Shannon’s Information Theory
Claude E. Shannon (1948)
• Source coding: Data compression
• Cryptology: Data encryption
• Channel coding: Error detection/correction/concealment
Separation theorem:
Source coding, encryption, and channel coding may be separated without information
loss (note that the separation theorem holds for very long data sequences only)

15. 11
Tasks of Channel Coding
• Error detection and error correction
⇒ enhancement of error probability (data security) and/or
⇒ reduction of transmit power (enhancement of power efficiency)
• Error concealment
(in conjunction with source coding)
⇒ improvement of subjective performance
• Unequal error protection
(in conjunction with source coding)
⇒ reduction of the number of parity check symbols
12

16. 12
Fundamental Principles of Channel Coding
• Forward error correction (FEC):
In forward error correction schemes there is no feedback from the channel decoder
to the channel encoder.
• Automatic repeat request (ARQ):
In automatic repeat request schemes there is feedback from the channel decoder to
the channel encoder. For example, a code word may be repeated until the channel
decoder does not detect any error. Alternatively, additional parity bits may be
transmitted until the channel decoder does not detect any error. The additional
decoding delay is not tolerable in all transmission schemes, such as in real-time
speech transmission schemes.
Within this lecture our focus is on FEC techniques.

17. • Cyclic block codes, generator polynomial, parity check polynomial
16
Definition of Block Codes
We denote a sequence u := [u0, u1, . . . , uk−1] of k info symbols as an info word.
The info symbols ui, i = 0, 1, . . . k − 1, are defined over the alphabet {0, 1, . . . , q − 1},
where q is the number of elements (“cardinality”) of the symbol alphabet.
Definition (block code): An (n, k)q block encoder maps an info word
u = [u0, u1, . . . , uk−1] of length k onto a code word x := [x0, x1, . . . , xn−1]
of length n, where n > k.
The code symbols xi, i = 0, 1, . . . , n − 1, are assumed to be within the same alphabet
{0, 1, . . . , q − 1}.
The assignment of code words with respect to the info words is
• unambiguous and reversible: For each code word there is exactly one info word
• time invariant: The mapping rule does not change in time
• memoryless: Each info word effects only one code word

18. 17
Generation of a Block Code
u0 u1
x0 x1 xi ∈ {0, 1, . . . , q − 1}, 0 ≤ i ≤ n − 1
ui ∈ {0, 1, . . . , q − 1}, 0 ≤ i ≤ k − 1
u ∈ {0, 1, . . . , q − 1}k
x ∈ {0, 1, . . . , q − 1}n
xn−1
uk−1
. . .
. . .
Encoder
Code word
Info word
18

19. 18
Redundancy, Error Detection, Error Correction
A code C is the set of all qk
code words.
Since n symbols are needed in order to transmit k info symbols, where n > k, the code
contains redundancy, because only qk
of the qn
possible combinations are allowed.
This redundancy is used for error detection, error correction, or error
concealment by the receiver.
The transmitted (possibly erroneous or noisy) code words are denoted as received
words y. For hard-decision decoding yi ∈ {0, 1, . . . , q − 1}, i = 0, 1, . . . , n − 1,
by definition.
The ratio
R :=
k
n
< 1
is called code rate. The smaller the code rate, the larger is the redundancy given the
same length n of the code word. The bandwidth expansion is R−1
.
⇒ Trade-off between bandwidth efficiency and power efficiency.

20. 19
Systematic Codes
Definition (systematic code): A code is called systematic, if the mapping between
info symbols and code symbols is such that the info symbols are explicitly contained in
the code words.
The n − k remaining symbols are called parity check symbols
(q = 2: parity check bits).
Example 1: (3, 2)2 single parity check (SPC) code:
(q = 2, i.e., one symbol corresponds to one bit)
Info word u = [u0, u1] Code word x = [x0, x1, x2]
[00] [000]
[01] [011]
[10] [101]
[11] [110]
Parity check equation: u0 ⊕ u1 ⊕ x2 = 0 (⊕: modulo-q addition)
Code: C = {[000], [011], [101], [110]}
20

21. • Catastrophic convolutional encoders
66
Coded Transmission System with Convolutional Codes
s Convolutional
encoder
E Discrete
channel
Convolutional
decoder
E
uk xn yn ˆuk
uk: Info bits, uk ∈ {0, 1}
xn: Code bits, xn ∈ {0, 1}
yn: Received values, hard-decision dec.: yn ∈ {0, 1}, soft-decision dec.: yn ∈ IR
ˆuk: Decoded info bits, ˆuk ∈ {0, 1}
k: Index before encoder
n: Index after encoder

22. 67
Convolutional Codes
Convolutional codes are able to encode the info bits continuously.
We restrict ourselves to binary convolutional codes. The ratio between the number of
info bits and the number of code bits is called coding rate R.
In practice, information is typically transmitted block-wise, rather than continuously.
The number of info bits per block is denoted as K, i.e., the index before the encoder is
0 ≤ k ≤ K − 1.
The number of coded bits per block is denoted as N, i.e., the index after the encoder is
0 ≤ n ≤ N − 1.
68

23. 68
Shift Register Representation of a Binary, Non-Recursive
R = 1/2 Convolutional Encoder with 4 States
u u u
u
u
u uh
E
c c
T
EE
E
D D t
t
t
t
t
t
t
t
&%
'$
&%
'$
&%
'$
+ +
+
uk xnuk−1 uk−2
Memory length: ν = 2
Number of states: S = 2ν
x2,k
x1,k