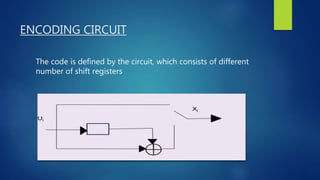
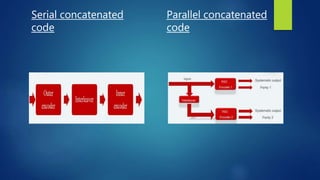
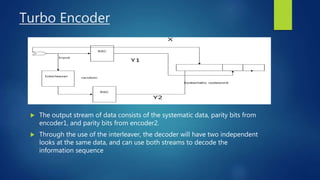
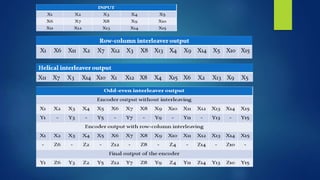
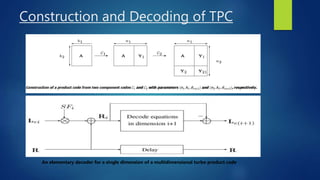
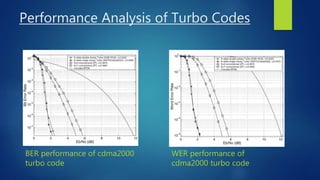
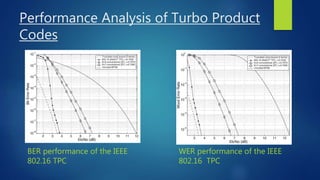
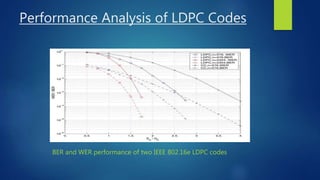
This document discusses turbo and turbo-like codes. It begins with an introduction to turbo codes, describing them as a class of high-performance error correction codes that were the first practical codes to closely approach channel capacity. It then covers channel coding, Shannon's theory, existing coding schemes like block codes and convolutional codes, and the need for better codes. The document spends significant time explaining turbo codes in detail, including their structure using parallel concatenated convolutional codes, interleaving, and iterative decoding. It also discusses related coding schemes like turbo product codes and low-density parity check codes. Finally, it reviews the performance, practical issues, applications in standards, and future trends of turbo and turbo-like codes.

1. Turbo and
Turbo-Like codes
SUDHANSHU SAINI
COMPUTER ENGINEERING (M.TECH)
(31803121)

2. Content:
 Introduction to Turbo Codes
 Channel Coding
 Shannon’s Theory
 FEC Coding Schemes
 A Need for Better Codes
 Turbo Codes
 Turbo-Like Codes
 Performance Analysis
 Practical Issues for Turbo FEC
 Turbo and Turbo-Like Codes in Standards
 Future Trends
 Conclusions
 References

3. Introduction to Turbo Codes
 In information theory, turbo codes are a class of high-
performance forward error correction (FEC) codes developed around
1990–91 (but first published in 1993), which were the first practical codes
to closely approach the channel capacity.
 Turbo codes achieve their remarkable performance with relatively low
complexity encoding and decoding algorithms.

4. Channel Coding
 To encode the information sent over a communication channel in such a
way that in the presence of channel noise, errors can be detected and/or
corrected.
 It Can be categorized into:
1. Backward error correction (BEC)
2. Forward error correction (FEC )

5. Shannon’s Theory
 For every combination of bandwidth (W), channel type, signal power (S)
and received noise power (N), there is a theoretical upper limit on the data
transmission rate R, for which error-free data transmission is possible. This
limit is called channel capacity or also Shannon capacity.
 It sets a limit to the energy efficiency of a code.
 A decibel is a relative measure. If E is the actual energy and Eref is the
theoretical lower bound, then the relative energy increase in decibels is

6. A Need for Better Codes
 Energy efficiency vs Bandwidth efficiency
 Codes with lower rate (i.e. bigger redundancy) correct more errors.then
communication system can operate with a lower transmit power, transmit
over longer distances, tolerate more interference, use smaller antennas
and transmit at a higher data rate. These properties make the code energy
efficient.
 Low-rate codes have a large overhead and are hence more heavy on
bandwidth consumption. Also, decoding complexity grows exponentially
with code length.

7. FEC Coding Schemes
 Block Codes
 Convolution Codes
 Concatenated Codes
 Low-Density Parity Check Codes

8. Block Codes
 A block code is any member of the large and important family of error-
correcting codes that encode data in blocks.
 Most common example is Hamming Code.
 Take a block of length ‘k’ (information sequence).
 Then encode them into a codeword , the last (n-k)bits are called Parity bits.
 Parity bits are used for error checking and correcting.

9. Convolution Codes
 Convolution codes are error detecting codes used to reliably transmit
digital data over unreliable communication channel system to channel
noise.
 The convolution codes map information to code bits , but sequentially
convolve the sequence of information bits according to some rule.
 Convolutional codes are often described as continuous.
 Viterbi and soft output Viterbi are most common.

10. ENCODING CIRCUIT
The code is defined by the circuit, which consists of different
number of shift registers

11. Cntd…
 We generate a convolution code by putting a source stream through a
linear filter. This filter makes use of a shift register, linear output functions
and possibly linear feedback.
 In a shift register, the information bits roll from right to left.
 In every filter there is one input bit and two output bits. Because of each
source bit having two transmitted bits, the codes have rate ½.

12. DEFINING CONVOLUTION CODE
 A convolution code can be defined by using a generator matrix that
describes the
encoding function u → x :
x = u .G
For 3 information bit long sequence u = (u0 ,u1 ,u2 )
we get
((x0 (1) x0 (2) ), (x1 (1)x1 (2) ), (x2 (1) x2 (2) )) = (u0 ,u1 ,u2 ) .G

13. PUNCTURING OF CONVOLUTION
CODES
 The idea of puncturing is to delete some bits in the code bit sequence according to a fixed
rule.
 In general the puncturing of a rate K / N code is defined using N puncturing vectors.
 Considering a code without puncturing, the information bit sequence
u =(0,0,1,1,0) generates the (unpunctured) code bit
sequence
xNP= (00,00,11,01,01). The sequence xNP is punctured using a
puncturing matrix:
PI= 1110
1001
 The puncturing period is 4. Using P1 , 3 out of 4 code .
 The performance of the punctured code is worse than the performance of the mother code.

14. DECODING CONVOLUTION CODES
 The most probable state sequence can be found using the min-sum
algorithm (also known as the Viterbi algorithm).
 The viterbi algorithm is used to decode convolutional codes and any
structure or system that can be described by a trellis.
 It is a maximum likelihood decoding algorithm that selects the most

15. Concatenated Codes
 Some times single error correction codes are not
good enough for error protection.
 Concatenating two or more codes will results more powerful
codes.
 Types of concatenated codes
1. Serial concatenated codes
2. Parallel concatenated codes

16. Serial concatenated
code
Parallel concatenated
code

17. Turbo Codes
 The Parallel-Concatenated Convolutional Codes(PCCC), called turbo
codes, has solved the dilemma of structure and randomness through
concatenation and interleaving respectively.
 The introduction of turbo codes has given most of the gain promised by
the channel coding theorem.
 Turbo codes have an astonishing performance of bit error rate (BER) at
relatively low Eb /No.

18. Turbo Encoder
 The output stream of data consists of the systematic data, parity bits from
encoder1, and parity bits from encoder2.
 Through the use of the interleaver, the decoder will have two independent
looks at the same data, and can use both streams to decode the
information sequence

19. Interleaver
 The interleaver’s function is to permute low weight code words in one
encoder into high weight code words for the other encoder.
 A “row-column” interleaver: data is written row-wise and read column
wise. While very simple, it also provides little randomness.
 A “helical” interleaver: data is written row-wise and read diagonally.
 An “odd-even” interleaver: first, the bits are left uninterleaved and
encoded , but only the odd-positioned coded bits are stored. Then, the
bits are scrambled and encoded, but now only the even-positioned coded
bits are stored. Odd-even encoders can be used, when the second encoder
produces one output bit per one input bit.

21. Recursive Systematic Coders
 Recursive codes are typically systematic.
 The example encoder is systematic because the input data is also used in
the output symbols.
 Recursive systematic convolutional (RSC) codes have become more
popular due to their use in Turbo Codes.

22. Turbo Decoding
 Criterion:
For n probabilistic processors working together to estimate common symbols, all
of them should agree on the symbols with the probabilities as a single decoder could do.
 The inputs to the decoders are the Log likelihood ratio (LLR) for the individual symbol d.
 LLR value for the symbol d is defined ( Berrou) as
 The SISO decoder reevaluates the LLR utilizing the local Y1 and Y2 redundancies to
improve the confidence .
 Compare the LLR output, to see if the estimate is towards 0 or 1 then take HD.

23. Cntd…
 The value z is the extrinsic value
determined by the same decoder and it
is negative if d is 0 and it is positive if d
is 1
 The updated LLR is fed into the other
decoder and which calculates the z and
updates the LLR for several iterations
 After several iterations , both decoders
converge to a value for that symbol.

24. Turbo Product Codes
 The serial concatenation of block codes separated by a structured
permutation (either implicit or explicit) was introduced in the 1950s. Codes
with this structure are referred to as product codes.
 Product codes may have many dimensions but are usually restricted to 2
or 3.
 Applying iterative decoding to such code structures results in TPCs, and
exchanging soft extrinsic information yields good performance.
 Iterative decoding of TPCs is performed by alternately decoding along the
different dimensions of the code, where again reliability information is
represented as true or approximate LLRs.
 Turbo Product Codes (TPCs) are based on block codes, not convolutional
codes.

25. Construction and Decoding of TPC
An elementary decoder for a single dimension of a multidimensional turbo product code

26. Low-Density Parity Check Codes
 Any linear block code can be defined by its parity-check matrix. If this
matrix is sparse, i.e it contains only a small number of 1s per row or
column, then the code is called a low-density parity-check code.
 Basically there are two different possibilities to represent LDPC codes:
─ Matrix Representation
─ Graphical Representation
 A regular LDPC matrix is an binary matrix having exactly Y ones in each
column and exactly ones in each row , where < and both are small
compared to m.
 If H is low-density but the number of 1’s in each row or column aren’t
constant the code is called a irregular LDPC code.

27. Representation
 Parity Check Matrix: (with dimension “ n × m ” for a (8 ,4)
code)
─ ρ = the number of 1‘s in each row
─ γ = the number of 1’s in each column
For a matrix to be called low-density the two conditions
γ<<n, ρ<<m must be satisfied.
 Bipartite Graph(so-called Tanner Graph): that means that
the nodes of the graph are separated into two distinctive
sets:
Variable nodes(v-nodes)
Check nodes(c-nodes)
─ m check nodes (the number of parity bits
─ n variable nodes (the number o bits in codeword

28. Turbo-Like Codes
 Some forms of turbo FEC do not fall neatly into any of the previous three
categories and are referred to as turbo-like codes.
 Hybrids of turbo codes and LDPC codes fall into this category.
 Convolutional codes are often used as the constituent codes, resulting in
serially concatenated convolutional codes (SCCCs).
 Decoding is performed in a manner similar to the parallel concatenated
case, iteratively applying SISO decoders for each constituent code.

29. Performance Analysis of Turbo Codes
BER performance of cdma2000
turbo code
WER performance of
cdma2000 turbo code

30. Performance Analysis of Turbo Product
Codes
BER performance of the IEEE
802.16 TPC
WER performance of the IEEE
802.16 TPC

31. Performance Analysis of LDPC Codes
BER and WER performance of two IEEE 802.16e LDPC codes

32. Practical Issues for Turbo FEC
 Error Rate Performance and Power Savings
 Computational Complexity
 Parallelism
 Memory Requirements
 Latency
 Flexibility
 Effect on Synchronization

33. TURBO OR TURBO-LIKE CODES IN
STANDARDS
 3G Wireless:
1. W-CDMA(Wideband code-division multiple-access)
2. CDMA2000
3. TD-SCDMA(Time-division, synchronous CDMA)
 Satellite Communications:
1. Consultative Committee for Space Data Systems (CCSDS)
2. Digital Video Broadcasting-Return Channel via Satellite
3. Digital Video Broadcasting via Satellite Second Generation
 Wireless Networking:
1. Wi-MAX (IEEE 802.16)
2. Wi-Fi (IEEE 802.11)

34. Future Trends
 Turbo and turbo-like codes will be widely used for at least the next decade
and probably substantially longer.
 No single class of turbo or turbo-like codes will dominate in the way that
convolutional codes and Viterbi decoding did in the past.
 Substantial improvements in computational efficiency and reductions in
unit costs are still possible.
 An increasing number of turbo and turbo-like codes will be tailored to
different channel conditions and system designs.
 The success of turbo FEC has led to the application of soft iterative
decoding techniques beyond channel coding.

35. Conclusions
 The advent of turbo and turbo-like codes has shown that excellent
performance, closely approaching the ultimate Shannon capacity limit for
an AWGN channel.
 It can be achieved through the soft iterative decoding of composite
channel codes.
 Implementing and using turbo and turbo-like codes in real systems does
present challenges, but tremendous progress in addressing these issues
has been made, and all varieties of turbo FEC are finding application.
 Turbo and turbo-like codes are no longer a curiosity or novelty, but a
powerful tool for improving the performance of communications systems.

36. THANK YOU!!!