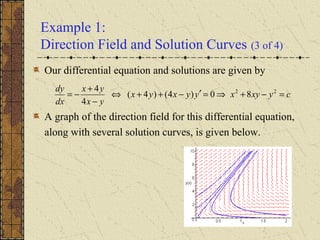
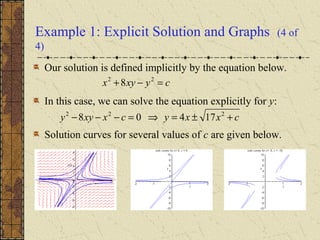
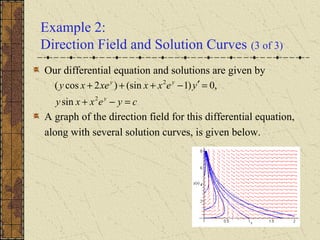
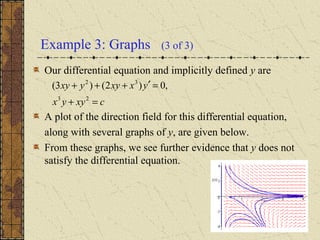
The document discusses exact and non-exact differential equations. It provides examples of first-order differential equations that are exact and can be solved implicitly using an integrating factor. It also gives an example of a non-exact equation, showing that attempting to solve it as if it were exact yields an incorrect solution. The document notes that a non-exact equation may be converted to an exact one by multiplying by a suitable integrating factor, which can sometimes be a function of just x or y.

1. Ch 2.6:
Exact Equations & Integrating Factors
Consider a first order ODE of the form
Suppose there is a function ψ such that
and such that ψ(x,y) = c defines y = φ(x) implicitly. Then
and hence the original ODE becomes
Thus ψ(x,y) = c defines a solution implicitly.
In this case, the ODE is said to be exact.
0),(),( =′+ yyxNyxM
),(),(),,(),( yxNyxyxMyx yx == ψψ
[ ])(,),(),( xx
dx
d
dx
dy
yx
yyxNyxM φψ
ψψ
=
∂
∂
+
∂
∂
=′+
[ ] 0)(, =xx
dx
d
φψ

2. Suppose an ODE can be written in the form
where the functions M, N, My and Nx are all continuous in the
rectangular region R: (x, y) ∈ (α, β ) x (γ, δ ). Then Eq. (1) is
an exact differential equation iff
That is, there exists a function ψ satisfying the conditions
iff M and N satisfy Equation (2).
)1(0),(),( =′+ yyxNyxM
)2(),(),,(),( RyxyxNyxM xy ∈∀=
)3(),(),(),,(),( yxNyxyxMyx yx == ψψ
Theorem 2.6.1

3. Example 1: Exact Equation (1 of 4)
Consider the following differential equation.
Then
and hence
From Theorem 2.6.1,
Thus
0)4()4(
4
4
=′−++⇔
−
+
−= yyxyx
yx
yx
dx
dy
yxyxNyxyxM −=+= 4),(,4),(
exactisODE),(4),( ⇒== yxNyxM xy
yxyxyxyx yx −=+= 4),(,4),( ψψ
( ) )(4
2
1
4),(),( 2
yCxyxdxyxdxyxyx x ++=+== ∫∫ψψ

4. Example 1: Solution (2 of 4)
We have
and
It follows that
Thus
By Theorem 2.6.1, the solution is given implicitly by
yxyxyxyx yx −=+= 4),(,4),( ψψ
( ) )(4
2
1
4),(),( 2
yCxyxdxyxdxyxyx x ++=+== ∫∫ψψ
kyyCyyCyCxyxyxy +−=⇒−=′⇒′+=−= 2
2
1
)()()(44),(ψ
kyxyxyx +−+= 22
2
1
4
2
1
),(ψ
cyxyx =−+ 22
8

5. Example 1:
Direction Field and Solution Curves (3 of 4)
Our differential equation and solutions are given by
A graph of the direction field for this differential equation,
along with several solution curves, is given below.
cyxyxyyxyx
yx
yx
dx
dy
=−+⇒=′−++⇔
−
+
−= 22
80)4()4(
4
4

6. Example 1: Explicit Solution and Graphs (4 of
4)
Our solution is defined implicitly by the equation below.
In this case, we can solve the equation explicitly for y:
Solution curves for several values of c are given below.
cxxycxxyy +±=⇒=−−− 222
17408
cyxyx =−+ 22
8

7. Example 2: Exact Equation (1 of 3)
Consider the following differential equation.
Then
and hence
From Theorem 2.6.1,
Thus
0)1(sin)2cos( 2
=′−+++ yexxxexy yy
1sin),(,2cos),( 2
−+=+= yy
exxyxNxexyyxM
exactisODE),(2cos),( ⇒=+= yxNxexyxM x
y
y
1sin),(,2cos),( 2
−+==+== y
y
y
x exxNyxxexyMyx ψψ
( ) )(sin2cos),(),( 2
yCexxydxxexydxyxyx yy
x ++=+== ∫∫ψψ

8. Example 2: Solution (2 of 3)
We have
and
It follows that
Thus
By Theorem 2.6.1, the solution is given implicitly by
1sin),(,2cos),( 2
−+==+== y
y
y
x exxNyxxexyMyx ψψ
( ) )(sin2cos),(),( 2
yCexxydxxexydxyxyx yy
x ++=+== ∫∫ψψ
kyyCyC
yCexxexxyx yy
y
+−=⇒−=′⇒
′++=−+=
)(1)(
)(sin1sin),( 22
ψ
kyexxyyx y
+−+= 2
sin),(ψ
cyexxy y
=−+ 2
sin

9. Example 2:
Direction Field and Solution Curves (3 of 3)
Our differential equation and solutions are given by
A graph of the direction field for this differential equation,
along with several solution curves, is given below.
cyexxy
yexxxexy
y
yy
=−+
=′−+++
2
2
sin
,0)1(sin)2cos(

10. Example 3: Non-Exact Equation (1 of 3)
Consider the following differential equation.
Then
and hence
To show that our differential equation cannot be solved by
this method, let us seek a function ψ such that
Thus
0)2()3( 32
=′+++ yxxyyxy
32
2),(,3),( xxyyxNyxyyxM +=+=
exactnotisODE),(3223),( 2
⇒=+≠+= yxNxyyxyxM xy
32
2),(,3),( xxyNyxyxyMyx yx +==+== ψψ
( ) )(2/33),(),( 222
yCxyyxdxyxydxyxyx x ++=+== ∫∫ψψ

11. Example 3: Non-Exact Equation (2 of 3)
We seek ψ such that
and
Then
Thus there is no such function ψ. However, if we
(incorrectly) proceed as before, we obtain
as our implicitly defined y, which is not a solution of ODE.
32
2),(,3),( xxyNyxyxyMyx yx +==+== ψψ
( ) )(2/33),(),( 222
yCxyyxdxyxydxyxyx x ++=+== ∫∫ψψ
kyxyxyCxxyC
yCxyxxxyyxy
+−=⇒−=′⇒
′++=+=
2/3)(2/3)(
)(22/32),(
23
??
23
?
23
ψ
cxyyx =+ 23

12. Example 3: Graphs (3 of 3)
Our differential equation and implicitly defined y are
A plot of the direction field for this differential equation,
along with several graphs of y, are given below.
From these graphs, we see further evidence that y does not
satisfy the differential equation.
cxyyx
yxxyyxy
=+
=′+++
23
32
,0)2()3(

13. It is sometimes possible to convert a differential equation
that is not exact into an exact equation by multiplying the
equation by a suitable integrating factor µ(x,y):
For this equation to be exact, we need
This partial differential equation may be difficult to solve. If
µ is a function of x alone, then µy = 0 and hence we solve
provided right side is a function of x only. Similarly if µ is a
function of y alone. See text for more details.
Integrating Factors
0),(),(),(),(
0),(),(
=′+
=′+
yyxNyxyxMyx
yyxNyxM
µµ
( ) ( ) ( ) 0=−+−⇔= µµµµµ xyxyxy NMNMNM
,µ
µ
N
NM
dx
d xy −
=

14. Example 4: Non-Exact Equation
Consider the following non-exact differential equation.
Seeking an integrating factor, we solve the linear equation
Multiplying our differential equation by µ, we obtain the
exact equation
which has its solutions given implicitly by
0)()3( 22
=′+++ yxyxyxy
xx
xdx
d
N
NM
dx
d xy
=⇒=⇔
−
= )(µ
µµ
µ
µ
,0)()3( 2322
=′+++ yyxxxyyx
cyxyx =+ 223
2
1