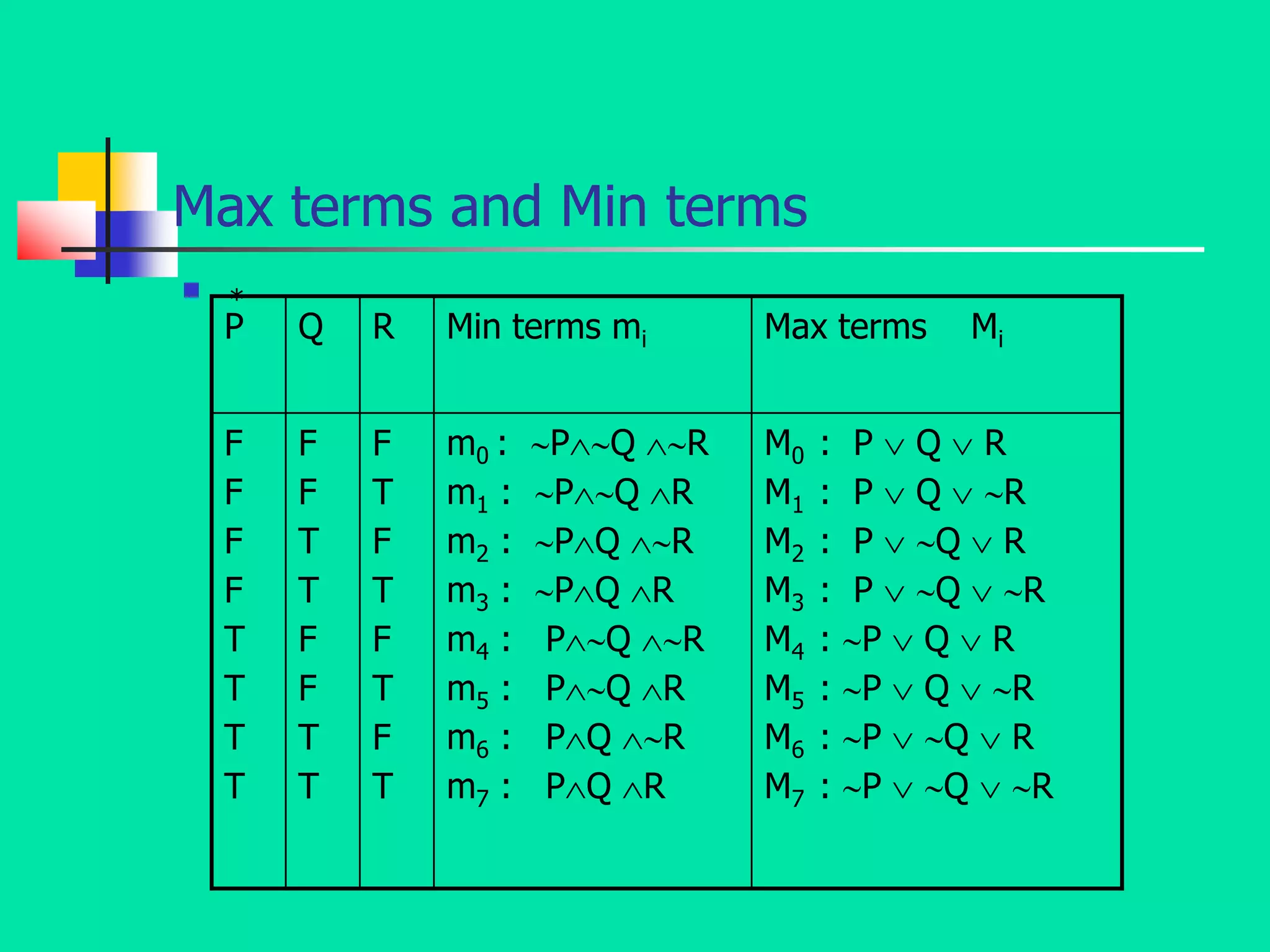
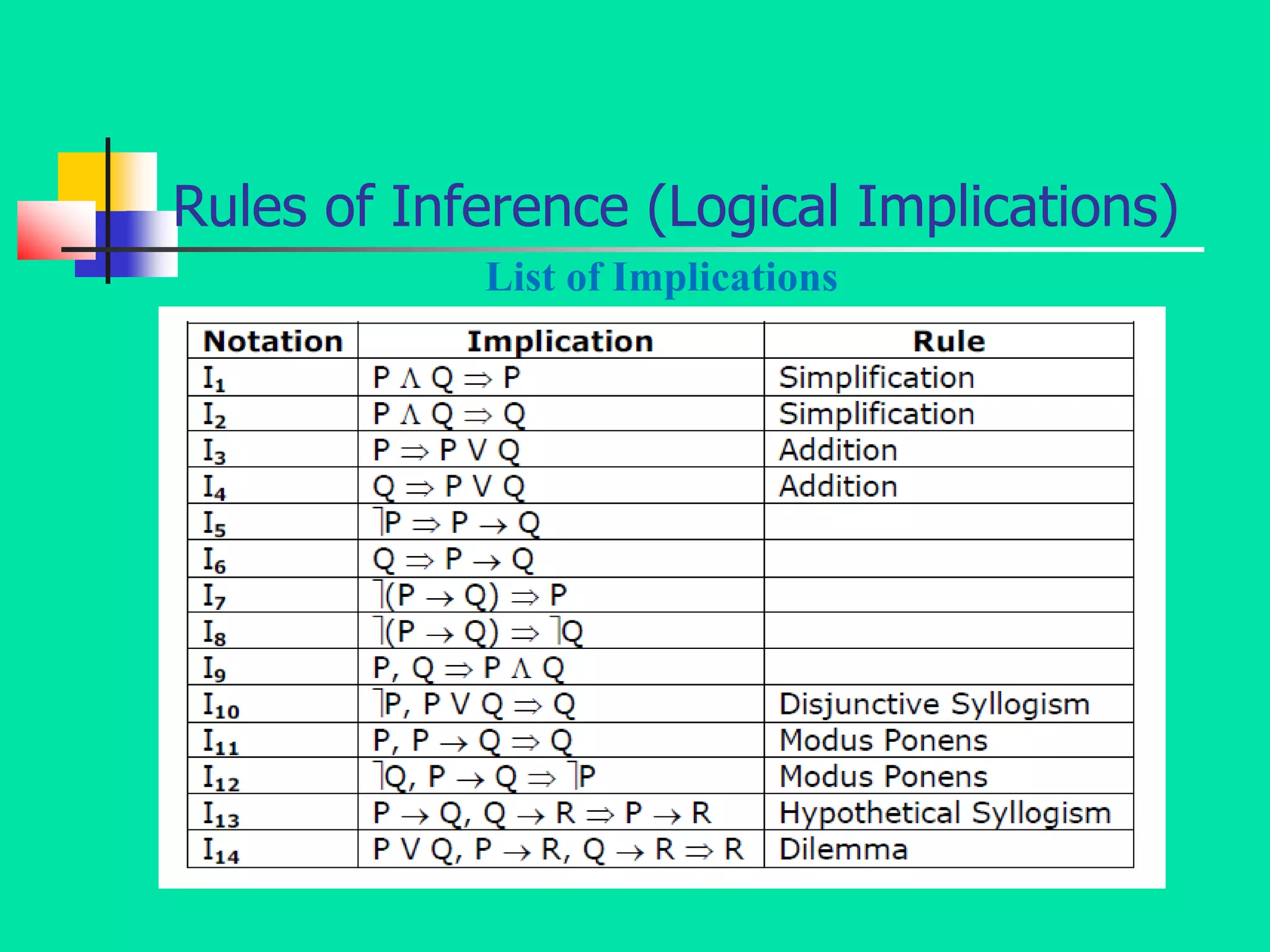
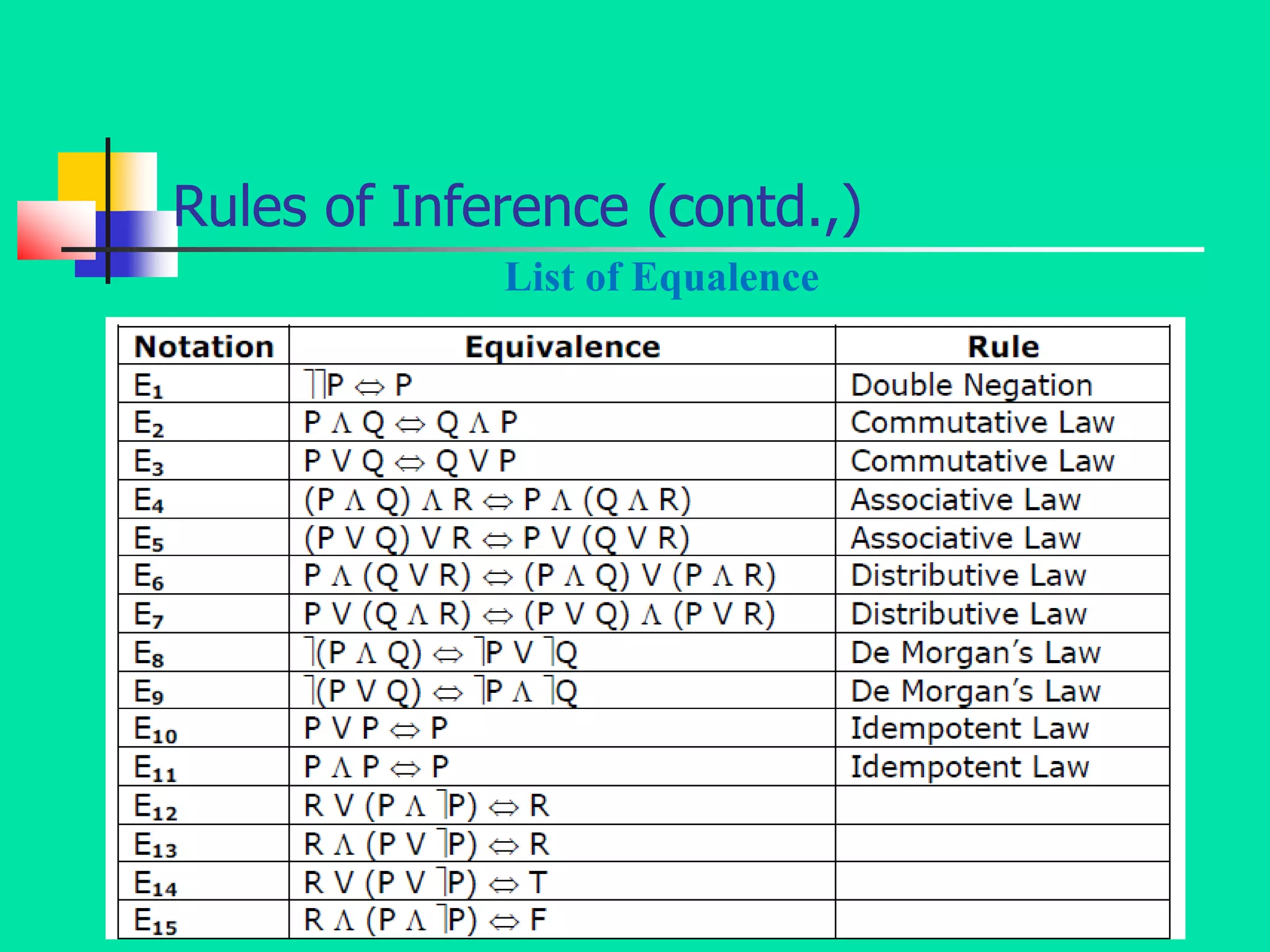
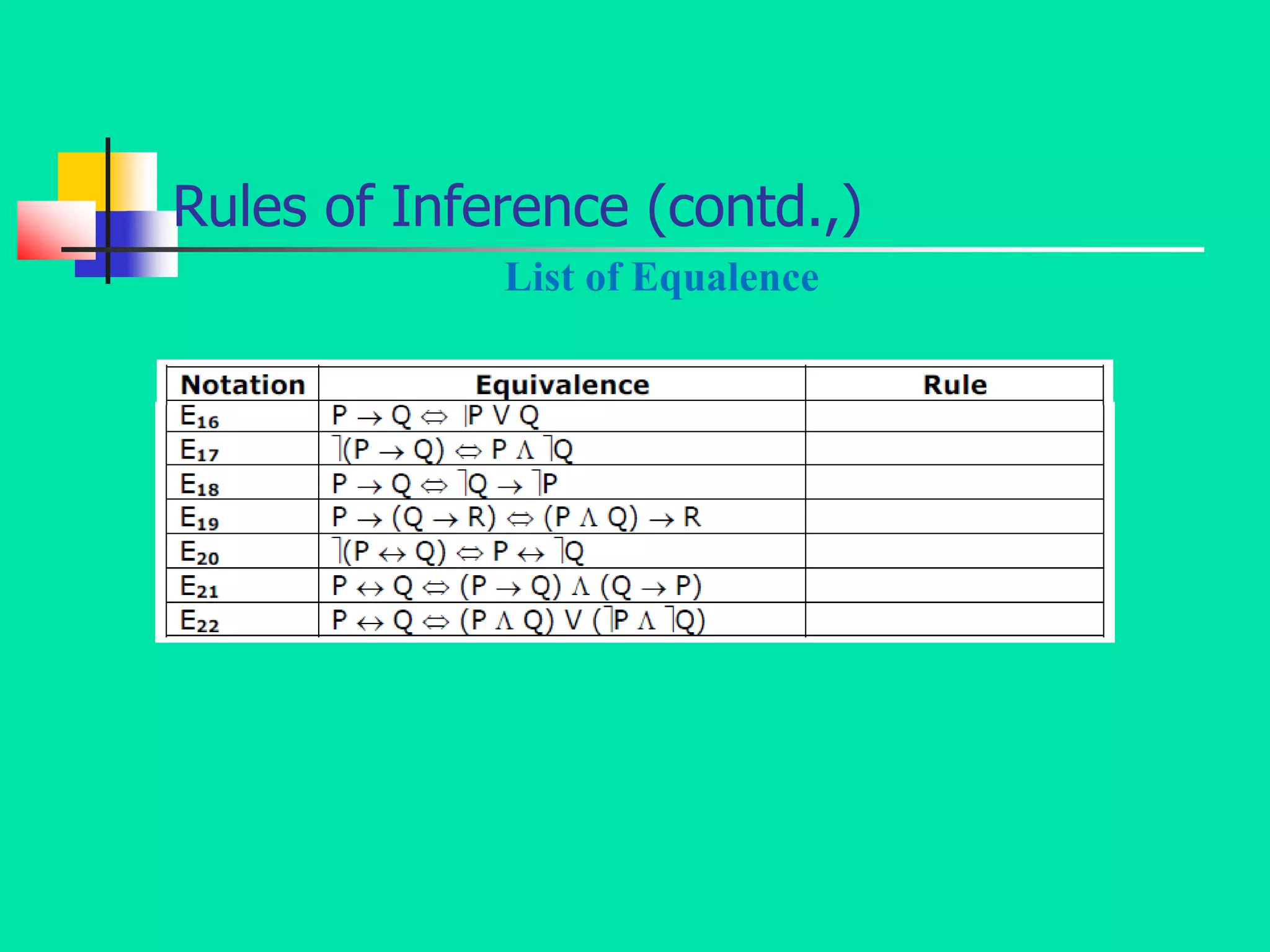
- The document discusses the mathematical foundations of computer science, including topics like mathematical logic, set theory, algebraic structures, and graph theory.
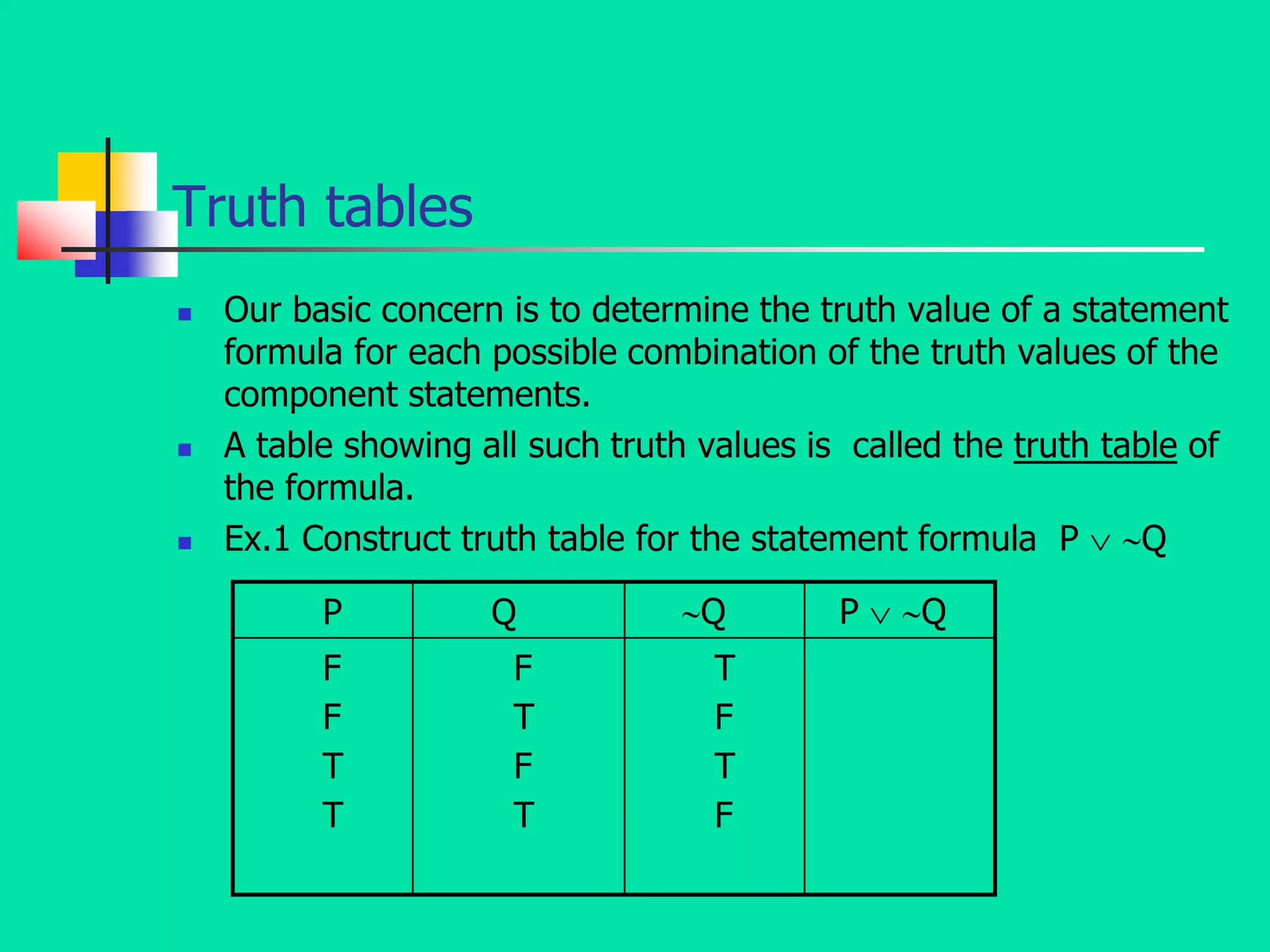
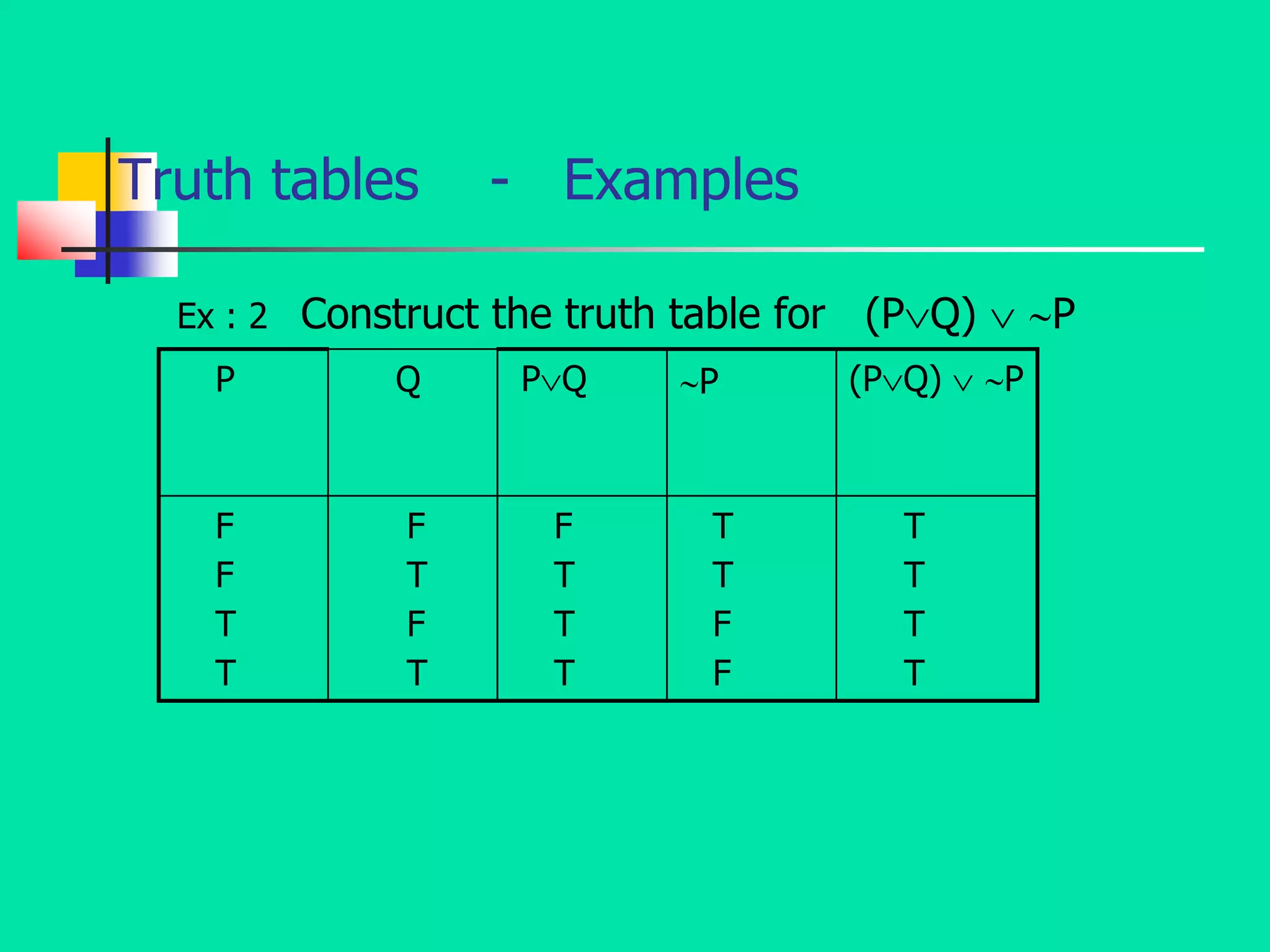
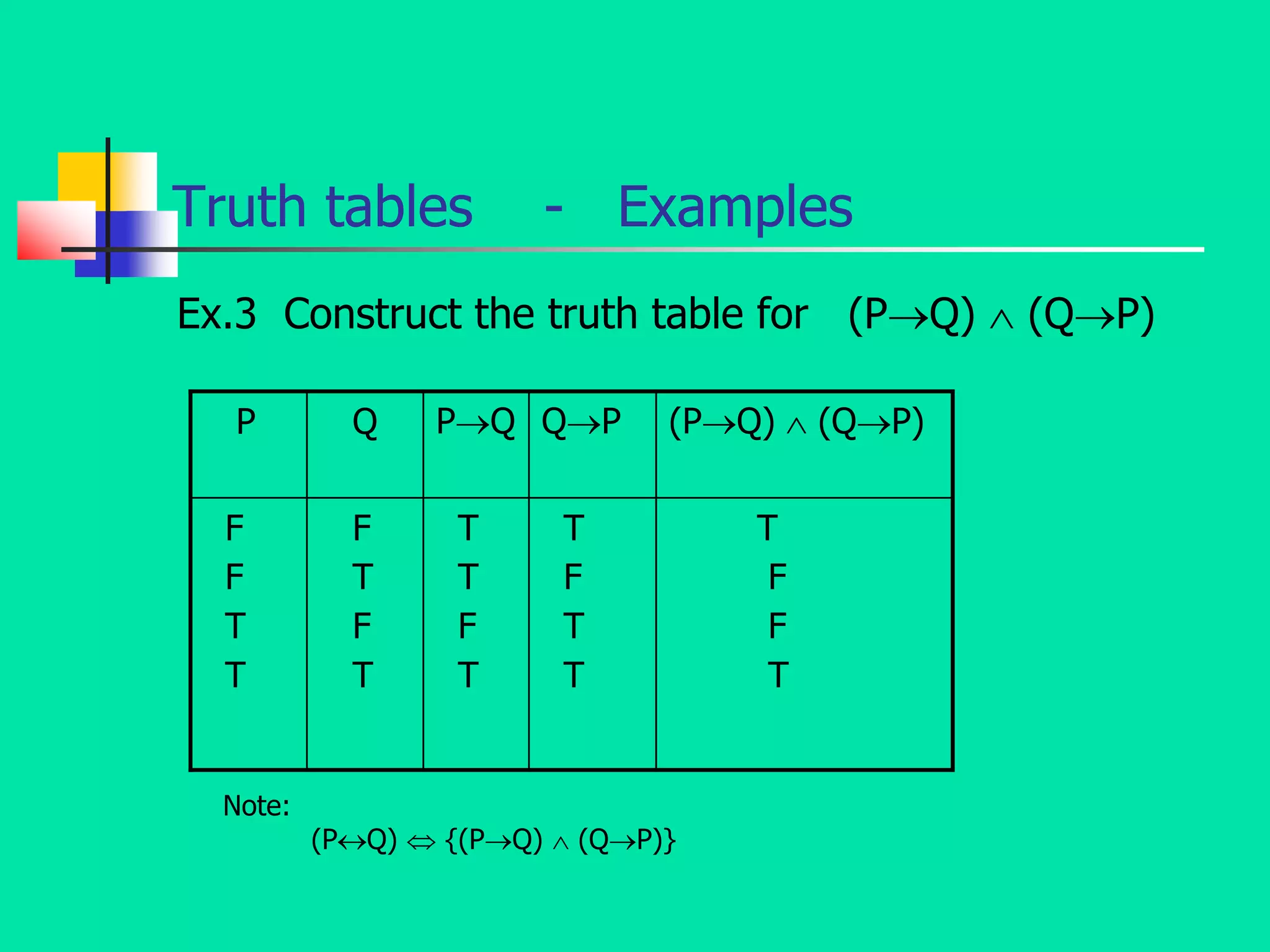
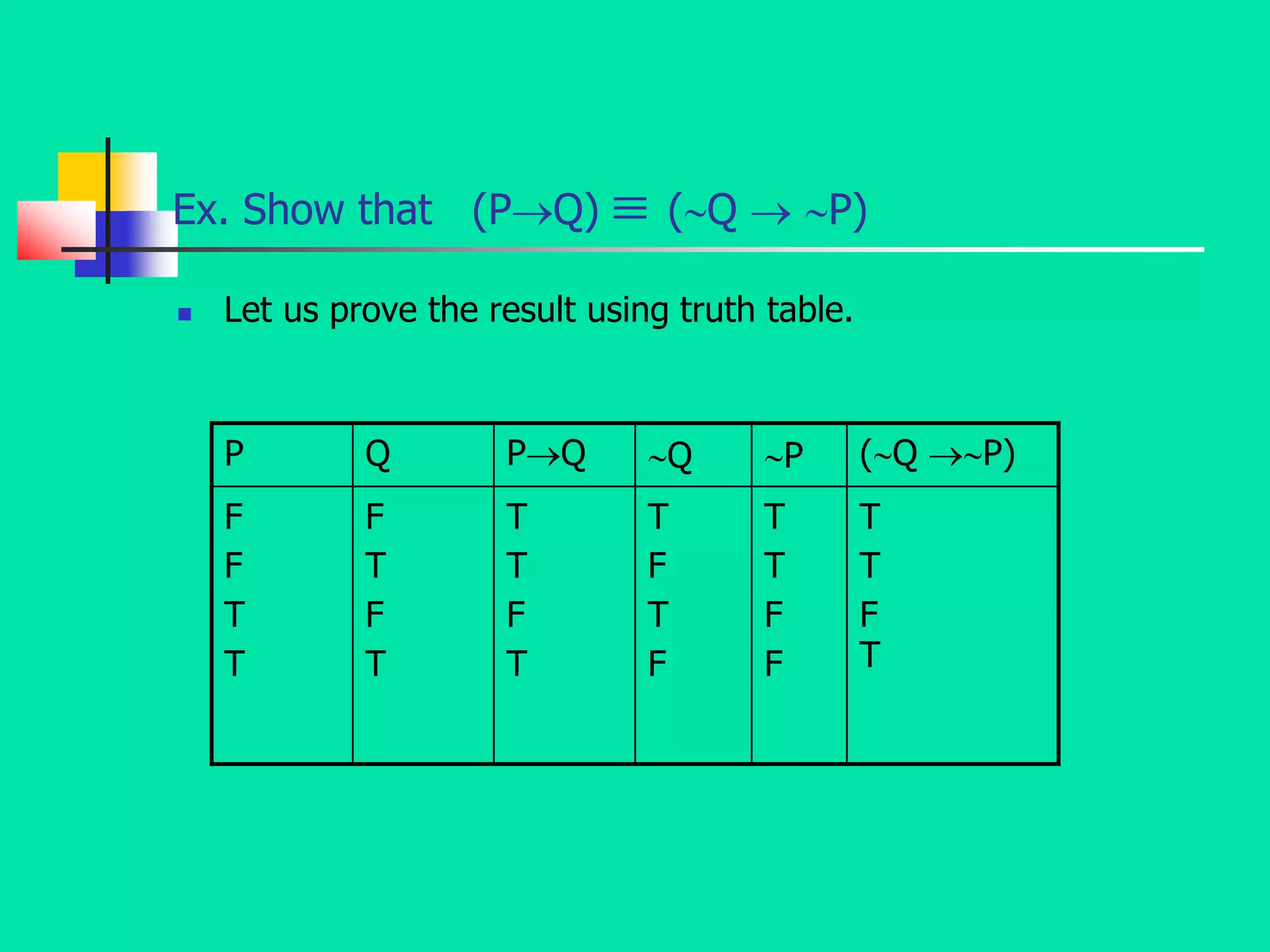
- It specifically focuses on mathematical logic, defining statements, atomic and compound statements, and various logical connectives like negation, conjunction, disjunction, implication, biconditional, and their truth tables.
- It also discusses logical concepts like tautologies, contradictions, contingencies, logical equivalence, and tautological implication through the use of truth tables and logical formulas.













![Ex.Construct truth table for [(pq) (r)] p]
The truth table is given below
p q r pq r (pq) (r) [(pq) (r)] p]
F F F
F F T
F T F
F T T
T F F
T F T
T T F
T T T
F
F
F
F
F
F
T
T
T
F
T
F
T
F
T
F
T
F
T
F
T
F
T
T
F
T
F
T
T
F
T
T](https://image.slidesharecdn.com/mathematicalfoundationsofcomputerscience-210214120432/75/Mathematical-foundations-of-computer-science-17-2048.jpg)



![More Equivalences
• P F P
• P T T
• P F F
• P T P
• P ( Q R) ( P Q ) R
( P Q ) (P Q)
• (P Q ) [( P Q) ( Q P )]
• ( P Q ) [( P Q) ( P Q )]
• Absorption laws
• P ( P Q ) P
• P ( P Q ) P](https://image.slidesharecdn.com/mathematicalfoundationsofcomputerscience-210214120432/75/Mathematical-foundations-of-computer-science-22-2048.jpg)



![Ex. Show that [{( P Q ) ( P Q )} R ] R
Proof: L.H.S = {( P Q ) ( P Q )} R
{ T } R (Since P Q ( P Q))
R
= R.H.S
Ex. Show that {( P Q ) ( P Q )} is a Contradiction.
Proof : Let P Q = R
Consider, {( P Q ) ( P Q )}
{ R R }
F
{ ( P Q ) ( P Q )} is a contradiction.](https://image.slidesharecdn.com/mathematicalfoundationsofcomputerscience-210214120432/75/Mathematical-foundations-of-computer-science-26-2048.jpg)

![Ex. S.T. ((P Q) (P (Q R))) ( P Q) (P R)
is a tautology.
Consider,
[(P Q) {P (Q R)}] {(P Q) (P R)}
[(P Q) {P (Q R)}] {(P Q) (P R)}
(By De morgan’s laws)
[(P Q) {P (Q R)}] {(P Q) (P R)}
(By De morgan’s laws)
[(P Q) {P Q) (P R)}] {(P Q) (P R)}
(By Distributive law)
{(P Q) (P R)} {(P Q) (P R)}
(Since A A A)
T ( Since A A T)](https://image.slidesharecdn.com/mathematicalfoundationsofcomputerscience-210214120432/75/Mathematical-foundations-of-computer-science-28-2048.jpg)




![Ex. Obtain the Principal Disjunctive normal form of the following
P {(PQ) (P Q)}
Given formula is, [ P {(PQ) (P Q)} ] = A (say)
The truth table for A is given below.
A (PQ) (PQ) (PQ)
Which is the PDNF for A .
P Q PQ P Q {(PQ)
(P Q)}
A
F
F
T
T
F
T
F
T
T
T
F
T
F
F
F
T
F
F
F
T
T
T
F
T](https://image.slidesharecdn.com/mathematicalfoundationsofcomputerscience-210214120432/75/Mathematical-foundations-of-computer-science-33-2048.jpg)