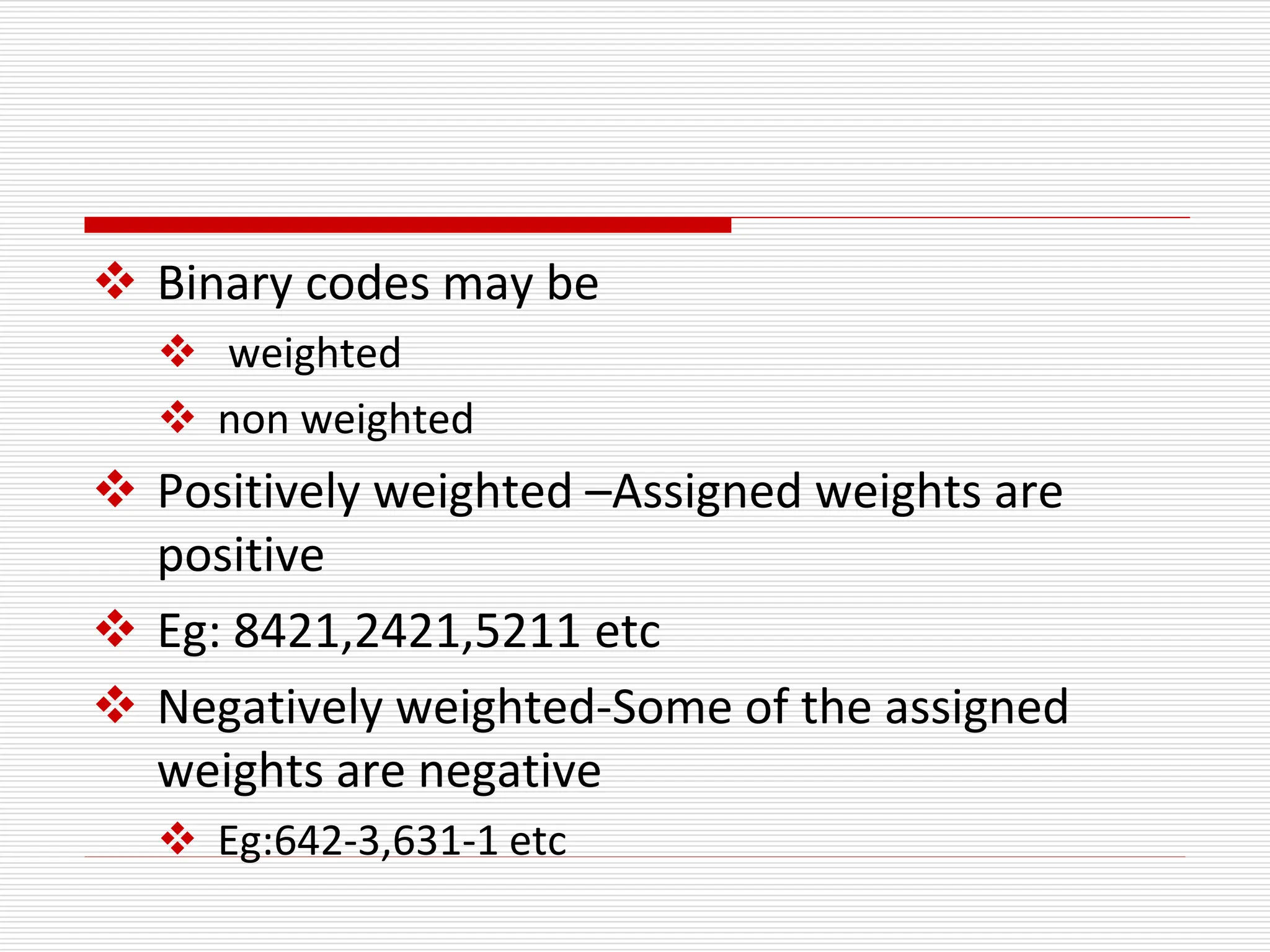
The document elaborates on binary codes, detailing their types including numeric and alphanumeric codes like ASCII and EBCDIC, as well as discussing error detection methods such as parity and Hamming codes. Various coding techniques for representing decimal digits in binary forms, including BCD and excess-3, along with operations for binary arithmetic and signed number representations, are also presented. Integral conversion processes between binary and gray codes are explained, alongside approaches for binary arithmetic operations.

1. Binary Codes
 Coding is the process of altering the characteristics
of information to make it more suitable for
intended application
 Representation of data using 0’s and 1’s is called
binary code
 Binary codes are classified as
 Numeric codes
 Eg: 8421,XS-3,Gray code
 Alphanumeric codes
 EBCDIC, ASCII

2.  Binary codes may be
 weighted
 non weighted
 Positively weighted –Assigned weights are
positive
 Eg: 8421,2421,5211 etc
 Negatively weighted-Some of the assigned
weights are negative
 Eg:642-3,631-1 etc

3.  Non weighted code
 Does not obey positional weighting
principle
 Eg: Excess 3 code(Xs-3), Gray code

4. BCD code( Binary Coded
Decimal)
 The digits of a decimal number are encoded into
groups of binary digits
 It is a weighted code
 The weights attached are 8,4,2,1
 Advantages
 Ease of conversion
 Disadvantage
 Less efficient than pure binary
 Invalid are : 1010,1011,1100,1101,1110,1111
Decimal digit 0 1 2 3 4
BCD 0000 0001 0010 0011 0100
Decimal digit 5 6 7 8 9
BCD 0101 0110 0111 1000 1001

5. Excess-3 (XS-3) code
 It is a non weighted code
 The binary code word of it is corresponding to
8421 +3
 Eg: 5= 0101 +0011 = 1000
 The invalid states are:
 0000,0001,0010,1101, 1110 &1111

6. Gray code
 This is a non weighted code
 It is not sutable for arithmetic operations
 It is cyclic
 Successive code differ in one bit position only
 Good for error detection.
Decimal Binary Gray Code Decimal Binary Gray code
0 0000 0000 8 1000 1100
1 0001 0001 9 1001 1101
2 0010 0011 10 1010 1111
3 0011 0010 11 1011 1110
4 0100 0110 12 1100 1010
5 0101 0111 13 1101 1011
6 0110 0101 14 1110 1001
7 0111 0100 15 1111 1000

7. Binary-to-Gray Code Conversion
 Retain most significant bit.
 From left to right, add each adjacent pair of binary
code bits to get the next Gray code bit, discarding
carries.
 Example: Convert binary number 10110 to Gray code.
 (10110)2 = 11101Gray
1 0 1 1 0 Binary

1 Gray
1 + 0 1 1 0 Binary

1 1 Gray
1 0 + 1 1 0 Binary

1 1 1 Gray
1 0 1 + 1 0 Binary

1 1 1 0 Gray
1 0 1 1 + 0 Binary

1 1 1 0 1 Gray

8. Gray-to-Binary Conversion
 Retain most significant bit.
 From left to right, add each binary code bit
generated to the Gray code bit in the next
position, discarding carries.
 Example: Convert Gray code 11011 to binary.
1 1 0 1 1 Gray

1 Binary
1 1 0 1 1 Gray
+ 
1 0 Binary
1 1 0 1 1 Gray
+ 
1 0 0 Binary
1 1 0 1 1 Gray
+ 
1 0 0 1 Binary
1 1 0 1 1 Gray
+ 
1 0 0 1 0 Binary
(11011)Gray = (10010)2

9. Alphanumeric Codes
 Apart from numbers, computers also handle textual data.
 Character set frequently used includes:
alphabets: ‘A’ .. ‘Z’, and ‘a’ .. ‘z’
digits: ‘0’ .. ‘9’
special symbols: ‘$’, ‘.’, ‘,’, ‘@’, ‘*’, …
non-printable: SOH, NULL, BELL, …
 Usually, these characters can be represented using 7 or 8
bits.
 Used for transmitting data between computers and i/o
devices
 Eg: ASCII,EBCDIC

10. ASCII (American standard Code for
Information Interchange)
 ASCII: 7-bit, plus a parity bit for error
detection (odd/even parity).
Character ASCII Code
0 0110000
1 0110001
. . . . . .
9 0111001
: 0111010
A 1000001
B 1000010
. . . . . .
Z 1011010
[ 1011011
1011100

11. ASCII
 ASCII table:
MSBs
LSBs 000 001 010 011 100 101 110 111
0000 NUL DLE SP 0 @ P ` p
0001 SOH DC1 ! 1 A Q a q
0010 STX DC2 “ 2 B R b r
0011 ETX DC3 # 3 C S c s
0100 EOT DC4 $ 4 D T d t
0101 ENQ NAK % 5 E U e u
0110 ACK SYN & 6 F V f v
0111 BEL ETB ‘ 7 G W g w
1000 BS CAN ( 8 H X h x
1001 HT EM ) 9 I Y i y
1010 LF SUB * : J Z j z
1011 VT ESC + ; K [ k {
1100 FF FS , < L l |
1101 CR GS - = M ] m }
1110 O RS . > N ^ n ~
1111 SI US / ? O _ o DEL

12. EBCDIC(Extended Binary Coded Decimal
Interchange code)
 It is an 8 bit alphanumeric code
 It can be used to encode all the symbols and
control characters
 Because 28= 256 bit patterns are available
A
I
R
C1
C9
D9
0
9
+
-
F0
F9
4E
6D

13. Error detecting and correcting code
 When data transmitted through a channel, due
to noise they may be get corrupted
 Error detection and correcting codes are used
to detect and correct errors
 Encoding may be done for error correction
and error detection.
 Eg: Parity code, Hamming code

14. Error Detecting Code (Parity)
 The simplest technique for detecting errors
 Implemented by adding an extra bit to each
word being transmitted
 Odd Parity – Set to a 0 or a 1 such that the total
number of 1 bits in the word including the parity
bit is an odd number
 Even Parity - Set to a 0 or a 1 such that the total
number of 1 bits in the word including the parity
bit is an even number

15. 7 bit Hamming Code (Error correcting)
 Three parity bits are added to transmit four
data bits
 Parity is added at bit positions 20 (1),21 (2) and(
22 (4)
 The word formed is
 P1 P2 D3 P4 D5 D6 D7
 D is data bits
 P is parity bits

16. Hamming Code(2)
 P1 is set to 0 or 1, so that it establishes even
parity over the bits 1,3,5,7(p1,d3,d5,d7)
 P2 is set to 0 or 1, so that it establishes even
parity over the bits 2,3,6,7(p2,d3,d6,d7)
 P4 is set to 0 or 1, so that it establishes even
parity over the bits 4,5,6,7(p4,d5,d6,d7)

17. Hamming code(3)
Eg:
 Encode 0011 to hamming code
P1 P2 D3 P4 D5 D6 D7
0 0 1 1
P1(P1,D3,D5,D7)-P1 001 1
P2(P2,D3,D6,D7)-P2 011 0
P4(P4,D5,D6,D7)-P4 011 0
Final code is 1000011

18. Decoding of Hamming code
 At the receiving end the hamming code is
decoded
 Bits 1,3,5,7 bits 2,3,6,7 and bits 4,5,6,7 are
checked
 If an error
 A three bit binary number is generated out of
the parity checks and error bit is complimented

19. Received word 1001001
 (1,3,5,7)- 1001 no error – put 0 in 1’s position
 (2,3,6,7)- 0001 error – put 1 in 2’s position
 (4,5,6,7)- 1001 no error – put 0 in 4’s position
 Error word is 010(2)
 Compliment 2nd bit
 Correct code is 1101001

20. Binary Arithmetic Operations (1/6)
 ADDITION
 Like decimal numbers, two numbers can be
added by adding each pair of digits together
with carry propagation.
(11011)2
+ (10011)2
(101110)2
2710
+ 1910
----------------
4610

21. Binary Arithmetic Operations (2/6)
 Digit addition table:
BINARY DECIMAL
0 + 0 + 0 = 0 0 0 + 0 + 0 = 0 0
0 + 1 + 0 = 0 1 0 + 1 + 0 = 0 1
1 + 0 + 0 = 0 1 0 + 2 + 0 = 0 2
1 + 1 + 0 = 1 0 …
0 + 0 + 1 = 0 1 1 + 8 + 0 = 0 9
0 + 1 + 1 = 1 0 1 + 9 + 0 = 1 0
1 + 0 + 1 = 1 0 …
1 + 1 + 1 = 1 1 9 + 9 + 1 = 1 9
0
1
1
0
1
Carry
in Carry
out
(11011)2
+ (10011)2
(101110)2
1
1
1
1
1
1
0
0
1
0
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0

22. Binary Arithmetic Operations (3/6)
 SUBTRACTION
 Two numbers can be subtracted by subtracting
each pair of digits together with borrowing,
where needed.
(11001)2
- (10011)2
(00110)2
(627)10
- (537)10
(090)10

23. Binary Arithmetic Operations (4/6)
 Digit subtraction table:
BINARY DECIMAL
0 - 0 - 0 = 0 0 0 - 0 - 0 = 0 0
0 - 1 - 0 = 1 1 0 - 1 - 0 = 1 9
1 - 0 - 0 = 0 1 0 - 2 - 0 = 1 8
1 - 1 - 0 = 0 0 …
0 - 0 - 1 = 1 1 0 - 9 - 1 = 1 0
0 - 1 - 1 = 1 0 1 - 0 - 1 = 0 0
1 - 0 - 1 = 0 0 …
1 - 1 - 1 = 1 1 9 - 9 - 1 = 1 9
Borro
w
(11001)2
- (10011)2
(00110)2
0
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
0
0
0
1
1
0
0
0
0
0
0
0

24. Binary Arithmetic Operations (5/6)
 MULTIPLICATION
 To multiply two numbers, take each digit of the multiplier
and multiply it with the multiplicand. This produces a
number of partial products which are then added.
(11001)2 (214)10 Multiplicand
x (10101)2 x (152)10 Multiplier
(11001)2 (428)10
(11001)2 (1070)10 Partial
+(11001)2 +(214)10 products
(1000001101)2 (32528)10 Result

25. Negative Numbers Representation
 Unsigned numbers: only non-negative values.
 Signed numbers: include all values (positive and negative).
 Till now, we have only considered how unsigned (non-
negative) numbers can be represented.
 There are three common ways of representing signed
numbers
Sign-and-Magnitude
1s Complement
2s Complement

26. Negative Numbers: Sign-and-Magnitude
(1/4)
 Negative numbers are usually written by writing a
minus sign in front.
Example:
- (12)10 , - (1100)2
 In sign-and-magnitude representation, this sign is
usually represented by a bit:
0 for +
1 for -

27. Negative Numbers: Sign-and-Magnitude
(2/4)
 Example: an 8-bit number can have 1-bit sign
and 7-bit magnitude.
sign magnitude

28. Negative Numbers: Sign-and-Magnitude
(3/4)
 Largest Positive Number: 0 1111111 +(127)10
 Largest Negative Number: 1 1111111 -(127)10
 Zeroes: 0 0000000 +(0)10
1 0000000 -(0)10
 Range: -(127)10 to +(127)10
 Question: For an n-bit sign-and-magnitude
representation, what is the range of values that
can be represented?

29. Negative Numbers:Sign-and-Magnitude
(4/4)
 To negate a number, just invert the sign bit.
 Examples:
- (0 0100001)sm = (1 0100001)sm
- (1 0000101)sm = (0 0000101)sm

30. 1s and 2s Complement
Two other ways of representing signed numbers for
binary numbers are:
 1s-complement
 2s-complement
They are preferred over the simple sign-and-
magnitude representation.

31. 1s Complement (1/2)
 Essential technique: invert all the bits.
Examples: 1s complement of (00000001)1s = (11111110)1s
1s complement of (01111111)1s = (10000000)1s
 Largest Positive Number: 0 1111111 +(127)10
 Largest Negative Number: 1 0000000 -(127)10
 Zeroes: 0 0000000
1 1111111
 Range: -(127)10 to +(127)10
 The most significant bit still represents the sign:
0 = +ve; 1 = -ve.

32. 1s Complement (2/2)
 Examples (assuming 8-bit binary numbers):
(14)10 = (00001110)2
-(14)10 = -(00001110)2 = (11110001)1s
-(80)10 = -( ? )2 = ( ? )1s

33. 1’s compliment subtraction
 Represent the number in true binary form
 Add 1’s compliment of subtrahend to the minuend
 If a carry, bring the carry around and add it to the
LSB
 Look at the sign bit , If it is 0 result is positive and in
true binary
 If MSB is 1, the result is negative and is in 1’s
compliment form
 Take 1’s compliment to get the magnitude in binary

34.  46-14
+14 00001110
-14 11110001
46 00101110
-14 + 11110001
----------------------
+32 1 00100000 Add carry to LSB
Example

35. 2s Complement (2/4)
 Essential technique: invert all the bits and add
1.
Examples:
2s complement of
(00000001)2s = (11111110)1s (invert)
= (11111111)2s (add 1)
2s complement of
(01111110)2s = (10000001)1s (invert)
= (10000010)2s (add 1)

36. 2s Complement (3/4)
 Largest Positive Number: 0 1111111
+(127)10
 Largest Negative Number: 1 0000000 -(128)10
 (special Case)
 Zero: 0 0000000
 Range: -(128)10 to +(127)10
 The most significant bit still represents the sign:
 0 = +ve; 1 = -ve.

37. 2s Complement (4/4)
 Examples (assuming 8-bit binary numbers):
(14)10 = (00001110)2
-(14)10 = -(00001110)2 = (11110010)2s
-(80)10 = -( ? )2 = ( ? )2s

38. 2’ compliment subtraction
 Add the 2’s compliment of subtrahend to the
minuend
 If there is a carry ignore it
 If MSB is 0, result is positive and in true binary
form
 If MSB is a 1 result is negative and is in 2’s
compliment form
 Take 2’s compliment

39. Example
 46-14
+14 00001110
-14 11110010
+46 00101110
-14 +11110010
----------------------
+32 100100000(Ignore carry)