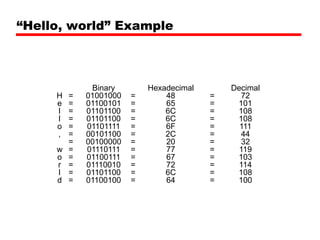
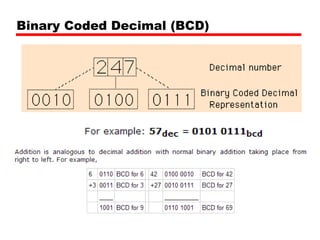
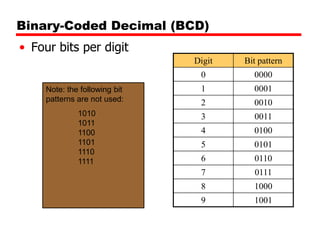
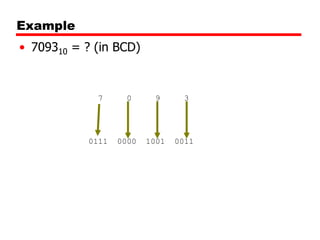
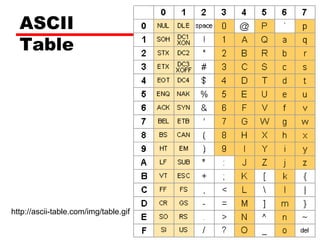
The document discusses different types of digital codes including binary coded decimal (BCD), Gray code, and alphanumeric codes like ASCII. BCD represents each decimal digit with a 4-bit binary pattern. Gray code minimizes bit changes between consecutive codes to reduce errors. ASCII is the most common alphanumeric code that assigns numbers to letters, punctuation, and controls. It uses 7-bit codes with the 8th bit sometimes used for parity.

1. Applied physics III
Digital Codes
by Benson Mbuya

2. Binary Coded Decimal (BCD)
• One of the most widely used representations of
numerical data is the binary coded decimal
(BCD) form in which each integer of a decimal
number is represented by a 4-bit binary number
(see conversion table).
• It is particularly useful for the driving of display
devices where a decimal output is desired. BCD
usually refers to such coding in which the binary
digits have their normal values, i.e., 8421.
Sometimes it is written "8421 BCD" to clearly
distinguish it from other binary codes such as
the4221 Code, but when BCD is used without
qualification, the 8421 version is assumed.

3. Binary Coded Decimal (BCD)

4. Binary-Coded Decimal (BCD)
• Four bits per digit
Digit
Bit pattern
0
0000
Note: the following bit
patterns are not used:
1
0001
2
0010
1010
1011
1100
1101
1110
1111
3
0011
4
0100
5
0101
6
0110
7
0111
8
1000
9
1001

5. Example
• 709310 = ? (in BCD)
7
0
9
3
0111
0000
1001
0011

6. BCD

7. BCD Addition
• Multi-digit BCD numbers can be added together
23
0010 0011
45
0100 0101
68
0110 1000
23
0010 0011
48
0100 1000
71
0110 1011
• 1011 is illegal BCD number

8. BCD Addition
• Add a 0110 (6) to an invalid BCD number
• Carry added to the most significant BCD digit
23
48
71
0010 0011
0100 1000
0110 1011
0110
0111 0001

9. 32
84
71
0011 0010
1000 0100
1011 0110
0110
10001 0110

10. Gray Code : Minimum Change code
• Gray code is also known as reflected binary code.
• The reflected binary code was originally designed to prevent
spurious outputs from electromechanical switches.
• Today, Gray codes are widely used to facilitate error correction in
digital communications

11. Gray code

13. Converting Gray coded number to binary

16. Example: binary to gray code

17. Example: Gray code to Binary

18. Alphanumeric Codes
• Represent numbers and alphabetic characters.
—Also represent other characters such as symbols and
various instructions necessary for conveying
information.
• The ASCII is the most common alphanumeric
code.
—ASCII = American Standard Code for Information
Interchange

19. The Problem
• Representing text strings, such as
“Hello, world”, in a computer

20. Codes and Characters
• Each character is coded as a byte
• Most common coding system is ASCII
(Pronounced ass-key)
• ASCII = American National Standard Code for
Information Interchange
• Defined in ANSI document X3.4-1977

21. ASCII Features
•
•
•
•
7-bit code
8th bit is unused (or used for a parity bit)
27 = 128 codes
Two general types of codes:
—95 are “Graphic” codes (displayable on a console)
—33 are “Control” codes (control features of the
console or communications channel)

22. ASCII
Table
http://ascii-table.com/img/table.gif

23. ASCII CHART
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
000
NULL
SOH
STX
ETX
EDT
ENQ
ACK
BEL
BS
HT
LF
VT
FF
CR
SO
SI
001
DLE
DC1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
010
!
"
#
$
%
&
'
(
)
*
+
,
.
/
011
0
1
2
3
4
5
6
7
8
9
:
;
<
=
>
?
100
@
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
101
P
Q
R
S
T
U
V
W
X
Y
Z
[
]
^
_
110
`
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
111
p
q
r
s
t
u
v
w
x
y
z
{
|
}
~
DEL

24. 000
001
0000
NULL
DLE
0001
SOH
DC1
0010
STX
DC2
0011
ETX
DC3
0100
EDT
DC4
0101
ENQ
NAK
0110
ACK
SYN
0111
BEL
ETB
1000
BS
CAN
1001
HT
EM
1010
LF
SUB
1011
VT
Least significantESC
bit
1100
FF
FS
1101
CR
GS
1110
SO
RS
1111
SI
US
010
011
0
!
1
"
2
#
3
Most significant bit
$
4
%
5
&
6
'
7
(
8
)
9
*
:
+
;
,
<
=
.
>
/
?
100
@
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
101
P
Q
R
S
T
U
V
W
X
Y
Z
[
]
^
_
110
`
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
111
p
q
r
s
t
u
v
w
x
y
z
{
|
}
~
DEL

25. e.g., ‘a’ = 1100001
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
000
NULL
SOH
STX
ETX
EDT
ENQ
ACK
BEL
BS
HT
LF
VT
FF
CR
SO
SI
001
DLE
DC1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
010
!
"
#
$
%
&
'
(
)
*
+
,
.
/
011
0
1
2
3
4
5
6
7
8
9
:
;
<
=
>
?
100
@
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
101
P
Q
R
S
T
U
V
W
X
Y
Z
[
]
^
_
110
`
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
111
p
q
r
s
t
u
v
w
x
y
z
{
|
}
~
DEL

26. 95 Graphic codes
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
000
NULL
SOH
STX
ETX
EDT
ENQ
ACK
BEL
BS
HT
LF
VT
FF
CR
SO
SI
001
DLE
DC1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
010
!
"
#
$
%
&
'
(
)
*
+
,
.
/
011
0
1
2
3
4
5
6
7
8
9
:
;
<
=
>
?
100
@
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
101
P
Q
R
S
T
U
V
W
X
Y
Z
[
]
^
_
110
`
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
111
p
q
r
s
t
u
v
w
x
y
z
{
|
}
~
DEL

27. 33 Control codes
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
000
NULL
SOH
STX
ETX
EDT
ENQ
ACK
BEL
BS
HT
LF
VT
FF
CR
SO
SI
001
DLE
DC1
DC2
DC3
DC4
NAK
SYN
ETB
CAN
EM
SUB
ESC
FS
GS
RS
US
010
!
"
#
$
%
&
'
(
)
*
+
,
.
/
011
0
1
2
3
4
5
6
7
8
9
:
;
<
=
>
?
100
@
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
101
P
Q
R
S
T
U
V
W
X
Y
Z
[
]
^
_
110
`
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
111
p
q
r
s
t
u
v
w
x
y
z
{
|
}
~
DEL

28. “Hello, world” Example
H
e
l
l
o
,
w
o
r
l
d
=
=
=
=
=
=
=
=
=
=
=
=
Binary
01001000
01100101
01101100
01101100
01101111
00101100
00100000
01110111
01100111
01110010
01101100
01100100
=
=
=
=
=
=
=
=
=
=
=
=
Hexadecimal
48
65
6C
6C
6F
2C
20
77
67
72
6C
64
=
=
=
=
=
=
=
=
=
=
=
=
Decimal
72
101
108
108
111
44
32
119
103
114
108
100

29. Extended ASCII
• There are an additional 128 characters that
were adopted by IBM for use in their PCs. It’s
popular and is used in applications other than
PCs  unofficial standard.
—The extended ASCII characters are represented by
an 8-bit code series from 80h-FFh

30. Extended
ASCII Table
http://ascii-table.com/img/table-pc.gif

31. Error Detection
• Digital Systems are very Reliable
• Errors during storage or transmission
• Parity Bit
—Even Parity
—Odd Parity

35. Odd Parity Error Detection
•
•
•
•
•
•
•
•
Original data
10011010
With Odd Parity
110011010
1-bit error
110111010
Number of 1s even indicates 1-bit error
2-bit error
110110010
Number of 1s odd no error indicated
3-bit error
100110010
Number of 1s even indicates error

36. BCD Addition
• Try these:
ex: Add the following numbers
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
0011+0100
00100011 + 00010101
10000110 + 00010011
010001010000 + 010000010111
1001 + 0100
1001 + 1001
00010110 + 00010101
01100111 + 01010011

38. references
• http://hyperphysics.phyastr.gsu.edu/hbase/electronic/number3.html
• http://hyperphysics.phyastr.gsu.edu/hbase/electronic/number3.html#c3
• http://autonopedia.org/crafts_and_technology/E
lectronics/DigitalBasics/codes.html