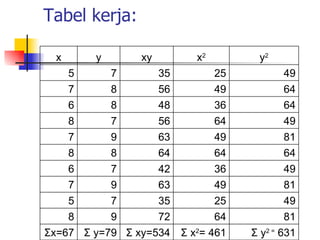
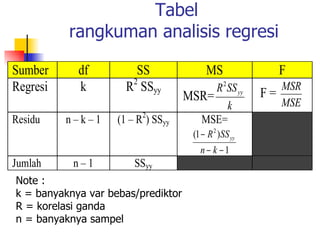
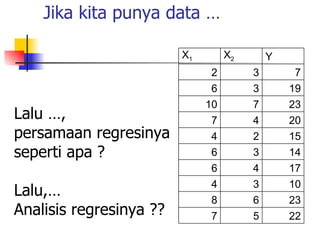
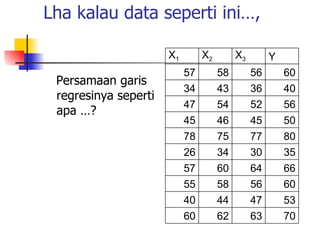
Dokumen tersebut membahas tentang analisis regresi, mulai dari penjelasan kapan diperlukan analisis regresi, regresi sederhana dengan satu variabel bebas, regresi ganda dengan dua atau lebih variabel bebas, serta contoh soal regresi sederhana dan ganda beserta penyelesaiannya.

6. Contoh : Data Nilai ulangan Harian (X) dan ulangan semester (Y) dari 10 siswa. Carilah persamaan regresi dan korelasinya ! 9 7 9 7 8 9 7 8 8 7 Y 8 5 7 6 8 7 8 6 7 5 X

7. Tabel kerja: Σ y 2 = 631 Σ x 2 = 461 Σ xy=534 Σ y=79 Σ x=67 81 64 72 9 8 49 25 35 7 5 81 49 63 9 7 49 36 42 7 6 64 64 64 8 8 81 49 63 9 7 49 64 56 7 8 64 36 48 8 6 64 49 56 8 7 49 25 35 7 5 y 2 x 2 xy y x

11. Analisis Varian Garis Regresi (Anareg)

13. Contoh dilanjutkan… Data Nilai ulangan Harian (X) dan ulangan semester (Y) dari 10 siswa. Buat anareg-nya ! Signifikan ? Solusi .. 9 7 9 7 8 9 7 8 8 7 Y 8 5 7 6 8 7 8 6 7 5 X

16. Tabel rangkuman analisis regresi Note : k = banyaknya var bebas/prediktor R = korelasi ganda n = banyaknya sampel

17. Jika kita punya data … Lalu …, persamaan regresinya seperti apa ? Lalu,… Analisis regresinya ?? 22 5 7 23 6 8 10 3 4 17 4 6 14 3 6 15 2 4 20 4 7 23 7 10 19 3 6 7 3 2 Y X 2 X 1