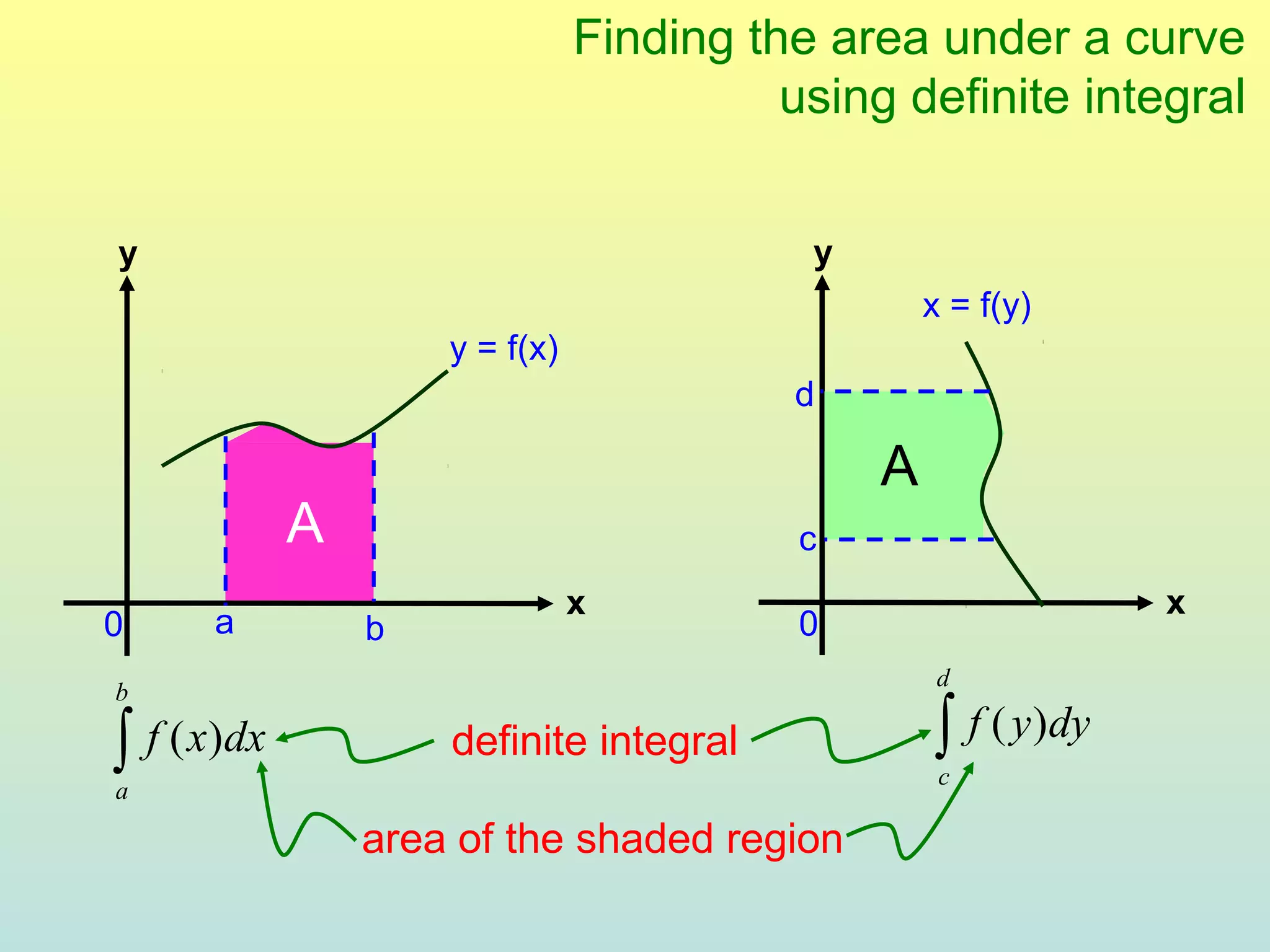
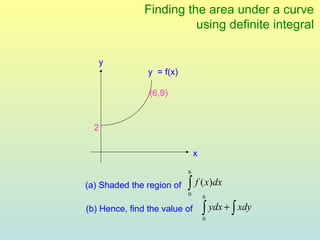
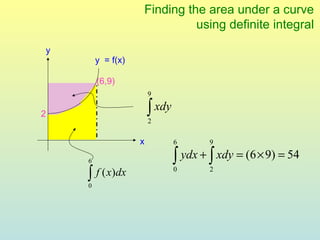
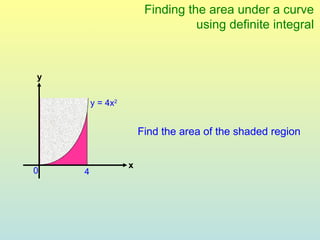
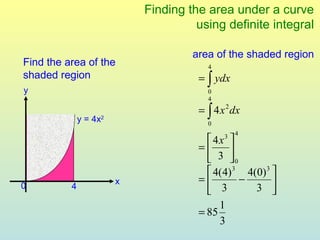
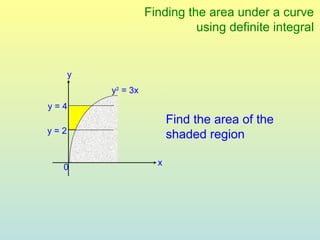
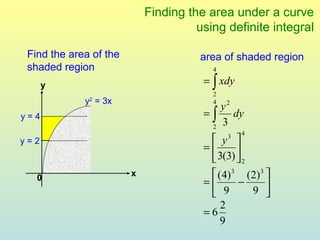
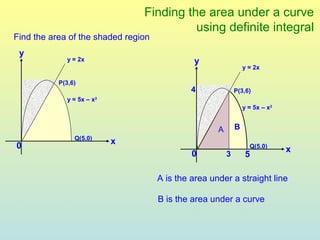
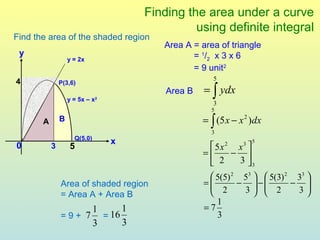
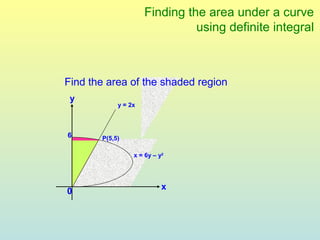
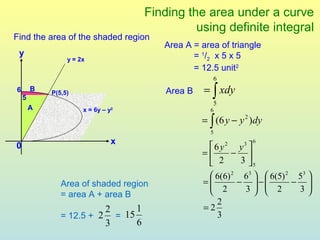
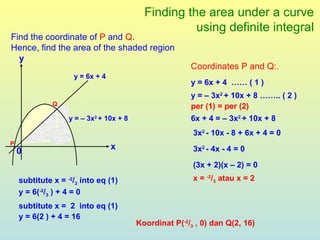
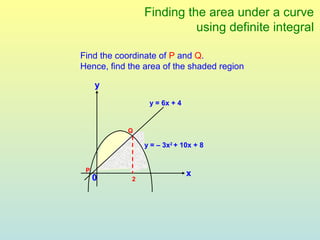
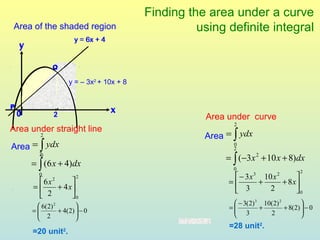
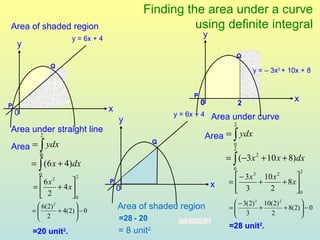
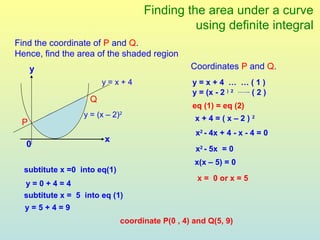
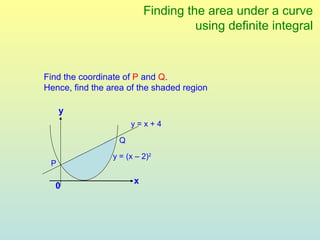
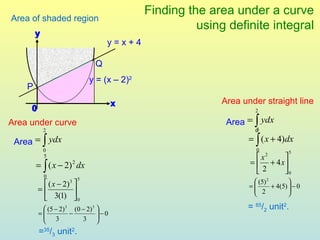
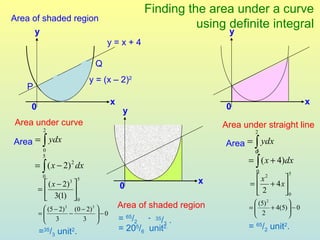
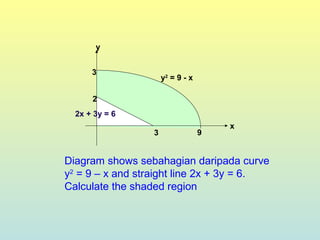
The document discusses using definite integrals to find the area under a curve. It provides examples of finding the area of various shaded regions bounded by curves and the x-axis using the formula: area = ∫f(x)dx from x=a to x=b. It also shows how to find the coordinates of points where two curves intersect in order to divide the region into multiple areas and calculate them separately.

1. Finding the area under a curve
using definite integral
y y
x = f(y)
y = f(x)
d
A
A c
x x
0 a b 0
d
b
∫ f ( x)dx definite integral ∫ f ( y)dy
c
a
area of the shaded region

2. Finding the area under a curve
using definite integral
y
y = f(x)
(6,9)
2
x
6
(a) Shaded the region of ∫ f ( x)dx
0 6
(b) Hence, find the value of ∫ ydx + ∫ xdy
0

3. Finding the area under a curve
using definite integral
y
y = f(x)
(6,9)
9
2 ∫ xdy
2
x 6 9
6 ∫ ydx + ∫ xdy = (6 × 9) = 54
∫
0
f ( x)dx 0 2

4. Finding the area under a curve
using definite integral
y
y = 4x2
Find the area of the shaded region
x
0 4

5. Finding the area under a curve
using definite integral
area of the shaded region
Find the area of the 4
shaded region = ∫ ydx
y 0
4
= ∫ 4 x 2 dx
y = 4x2 0
4
 4x 3
= 
 3 0
 4(4) 3 4(0) 3 
x = − 
0 4 3 3 

1
= 85
3

6. Finding the area under a curve
using definite integral
y
y2 = 3x
y=4
Find the area of the
y=2
shaded region
x
0

7. Finding the area under a curve
using definite integral
Find the area of the area of shaded region
shaded region 4
y = ∫ xdy
2
y = 3x
2
4
y2
y=4 = ∫ dy
2
3
4
y=2  y 3
= 
 3(3)  2
0
x  (4) 3 (2) 3 
= − 
 9 9 
2
=6
9

8. Finding the area under a curve
using definite integral
Find the area of the shaded region
y
y = 2x y
y = 2x
P(3,6)
4 P(3,6)
y = 5x – x2
y = 5x – x2
A B
Q(5,0)
x
0 Q(5,0)
x
0 3 5
A is the area under a straight line
B is the area under a curve

9. Finding the area under a curve
using definite integral
Find the area of the shaded region
Area A = area of triangle
y = 1/2 x 3 x 6
y = 2x
= 9 unit2
5
4 P(3,6)
Area B = ∫ ydx
y = 5x – x2
3
5
A B = ∫ (5 x − x 2 )dx
3
Q(5,0)
x 5
0 3 5  5x 2
x 
3
= − 
 2 3 3
 5(5) 2 53   5(3) 2 33 
Area of shaded region =
 2 − 3 − 2 − 3 
  
= Area A + Area B    
1
1 1 =7
= 9 + 7 = 16 3
3 3

10. Finding the area under a curve
using definite integral
Find the area of the shaded region
y
y = 2x
6 P(5,5)
y = 5x – x2
x = 6y – y2
A
x
0

11. Finding the area under a curve
using definite integral
Find the area of the shaded region
Area A = area of triangle
y = 1/2 x 5 x 5
y = 2x
= 12.5 unit2
6
6 B
P(5,5) Area B = ∫ xdy
5 y = 5x – x2
5
A x = 6y – y2 6
A = ∫ (6 y − y 2 )dy
5
x 6
0 6y 2
y 
3
= − 
 2 3 5
 6(6) 2 63   6(5) 2 53 
Area of shaded region =
 2 − 3 − 2 − 3 
  
= area A + area B    
2
2 1 =2
= 12.5 + 2 = 15 3
3 6

12. Finding the area under a curve
using definite integral
Find the coordinate of P and Q.
Hence, find the area of the shaded region
y
Coordinates P and Q:.
y = 6x + 4
y = 6x + 4 …… ( 1 )
y = – 3x2 + 10x + 8 …….. ( 2 )
Q per (1) = per (2)
y = – 3x2 + 10x + 8 6x + 4 = – 3x2 + 10x + 8
3x2 - 10x - 8 + 6x + 4 = 0
P
x 3x2 - 4x - 4 = 0
0
(3x + 2)(x – 2) = 0
subtitute x = -2/3 into eq (1) x = -2/3 atau x = 2
y = 6(-2/3 ) + 4 = 0
subtitute x = 2 into eq (1)
y = 6(2 ) + 4 = 16
Koordinat P(-2/3 , 0) dan Q(2, 16)

13. Finding the area under a curve
using definite integral
Find the coordinate of P and Q.
Hence, find the area of the shaded region
y
y = 6x + 4
Q
y = – 3x2 + 10x + 8
P
x
0 2

14. Finding the area under a curve
Area of the shaded region using definite integral
y = 6x + 4
y
Q
y = – 3x2 + 10x + 8
P
0 2
x
Area under curve
2
Area under straight line
2 Area = ∫ ydx
Area = ∫ ydx 0
2
= ∫ (−3 x 2 + 10 x + 8)dx
2
0
= ∫ (6 x + 4)dx 0 2
0 2  − 3 x 3 10 x 2 
 6x2  = + + 8x
= + 4 x  3 2 0
 2 0
 6(2)2
  − 3(2) 3 10(2) 2 
= + 4(2)  − 0 =
 3 + + 8(2)  − 0

 2   2 
 
=28 unit2.
=20 unit . 2

15. Finding the area under a curve
Area of shaded region using definite integral
y = 6x + 4
y
y
Q
Q
y = – 3x2 + 10x + 8
P
0 2
x
P
0 x
y = 6x + 4 Area under curve
y 2
Area under straight line
2 Area = ∫ ydx
Area = ∫ ydx
Q 0
2
= ∫ (−3 x 2 + 10 x + 8)dx
2
0
= ∫ (6 x + 4)dx 0 2
0 2  − 3 x 3 10 x 2 
 6x2  P
x = + + 8x
= + 4 x 0  3 2 0
 2 0
 − 3(2) 3 10(2) 2 
 6(2)
=
2

+ 4(2)  − 0
Area of shaded region =
 3 + + 8(2)  − 0

 2   2 
  =28 - 20
=28 unit2.
=20 unit . 2 = 8 unit 2.

16. Finding the area under a curve
using definite integral
Find the coordinate of P and Q.
Hence, find the area of the shaded region
y Coordinates P and Q.
y=x+4 y=x+4 … …(1)
y = (x - 2 ) 2 …….. ( 2 )
Q
eq (1) = eq (2)
y = (x – 2)2 x+4=(x–2)2
P
x2 - 4x + 4 - x - 4 = 0
x
0
x2 - 5x = 0
x(x – 5) = 0
subtitute x =0 into eq(1)
x = 0 or x = 5
y=0+4=4
subtitute x = 5 into eq (1)
y=5+4=9
coordinate P(0 , 4) and Q(5, 9)

17. Finding the area under a curve
using definite integral
Find the coordinate of P and Q.
Hence, find the area of the shaded region
y
y=x+4
Q
y = (x – 2)2
P
x
0

18. Finding the area under a curve
Area of shaded region
using definite integral
y
y=x+4
Q
y = (x – 2)2
P
x Area under straight line
0 2
Area under curve Area = ∫ ydx
2 5
0
Area = ∫ ydx = ∫ ( x + 4)dx
0 0 5
5  x2 
= ∫ ( x − 2) 2 dx =  + 4 x
2 0
0 5
 ( x − 2) 3   (5) 2 
= =
 2 + 4(5)  − 0

  
 3(1)  0
 (5 − 2) 3 (0 − 2)3  = 65/2 unit2.
=
 3 − 3 −0 
 
=35/3 unit2.

19. Finding the area under a curve
Area of shaded region
using definite integral
y y
y=x+4
Q
y = (x – 2)2
P
x x
0 y 0
Area under curve Area under straight line
2 2
Area = ∫ ydx Area = ∫ ydx
0 5
0
= ∫ ( x + 4)dx
5
= ∫ ( x − 2) 2 dx
0 5
0 5
x  x2 
 ( x − 2) 3  0 =  + 4 x
=  2 0
 3(1)  0
Area of shaded region  (5) 2 
 (5 − 2) 3 (0 − 2)3  =
 2 + 4(5)  − 0

=
 3 − 3 −0   
  = 65/2 - 35/3 .
= 205/6 unit2. = 65/2 unit2.
= /3 unit .
35 2

20. y
3
y2 = 9 - x
2
2x + 3y = 6
x
3 9
Diagram shows sebahagian daripada curve
y2 = 9 – x and straight line 2x + 3y = 6.
Calculate the shaded region

21. y
3 y2 = 9 - x
2
2x + 3y = 6
3 9 x
Area of shaded region = area under curve – area of triangle
3
1
= ∫ xdy − × 3 × 2
0
2
3
= ∫ (9 − y 2 )dy - 6
0
3
 y 3
= 9 y −  - 6
 3 0
33
= 9(3) − − 3 = 15
3