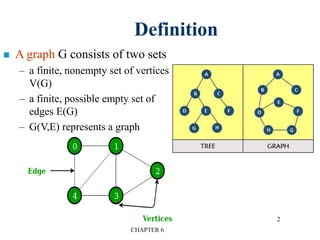
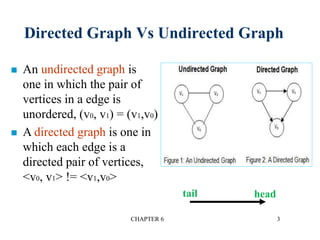
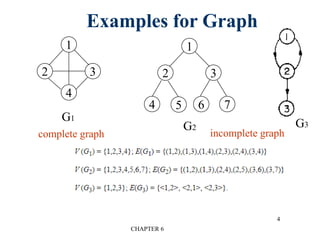
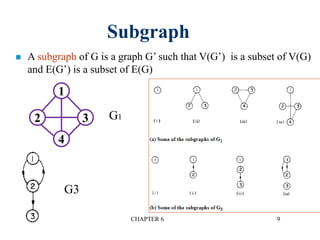
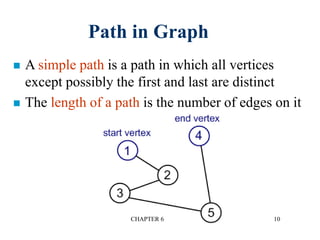
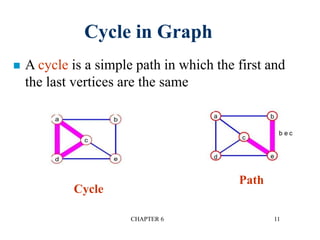
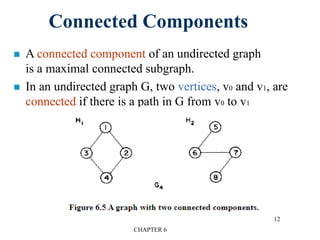
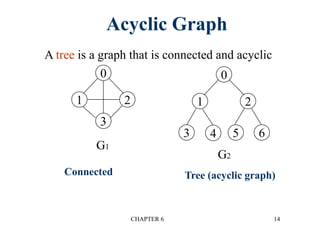
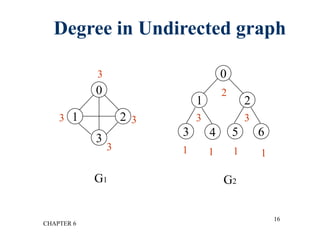
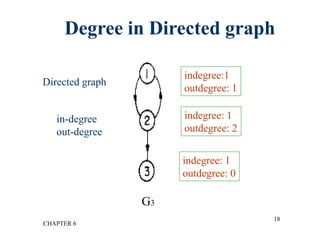
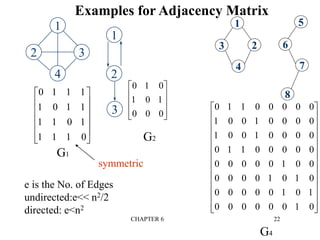
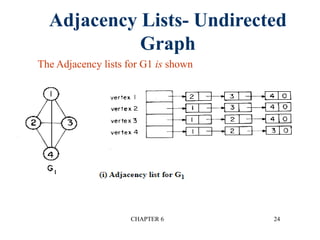
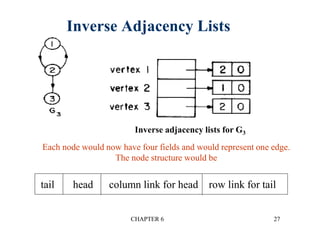
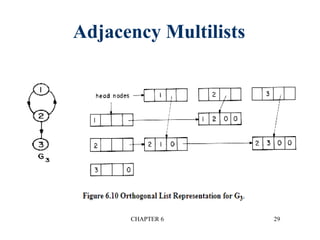
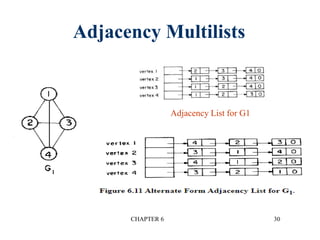
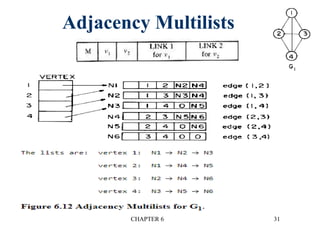
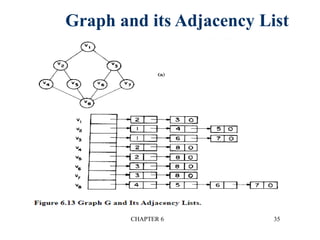
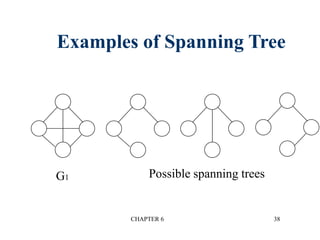
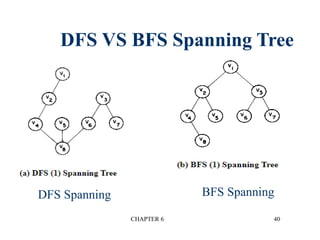
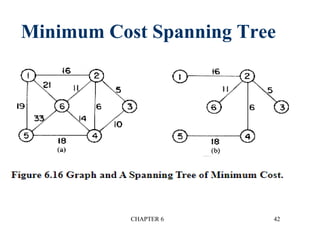
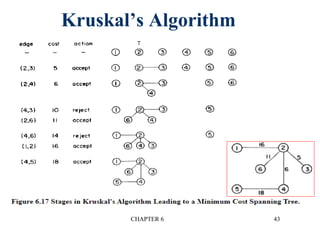
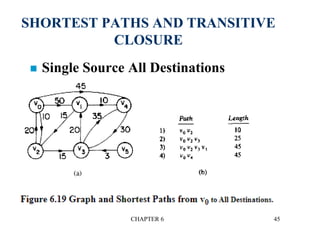
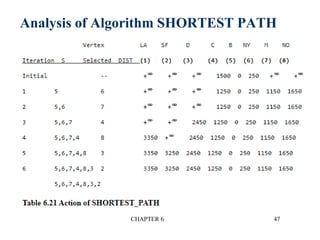
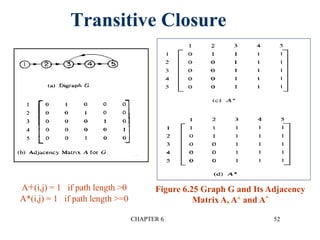
This document provides an overview of graphs and graph algorithms. It defines graphs, directed and undirected graphs, and graph terminology like vertices, edges, paths, cycles, connected components, and degrees. It describes different graph representations like adjacency matrices and adjacency lists. It also explains graph traversal algorithms like depth-first search and breadth-first search. Finally, it covers graph algorithms for finding minimum spanning trees, shortest paths, and transitive closure.

1. CHAPTER 6
GRAPHS
Dr. R. Khanchana
Assistant Professor
Department of Computer Science
Sri Ramakrishna College of Arts and Science for
Women
CHAPTER 6 1
http://icodeguru.com/vc/10book/books/book1/chap06.htm

2. CHAPTER 6
2
Definition
 A graph G consists of two sets
– a finite, nonempty set of vertices
V(G)
– a finite, possible empty set of
edges E(G)
– G(V,E) represents a graph

3. Directed Graph Vs Undirected Graph
CHAPTER 6 3
 An undirected graph is
one in which the pair of
vertices in a edge is
unordered, (v0, v1) = (v1,v0)
 A directed graph is one in
which each edge is a
directed pair of vertices,
<v0, v1> != <v1,v0>
tail head

4. CHAPTER 6
4
Examples for Graph
1
2 3
4
1
2 3
4 5 6 7
G1
G2 G3
complete graph incomplete graph

5. CHAPTER 6 5
Complete Graph
 A complete graph is a graph that has the
maximum number of edges
– for undirected graph with n vertices, the
maximum number of edges is n(n-1)/2
– for directed graph with n vertices, the
maximum number of edges is n(n-1)
– Example:
– G1 is a complete undirected graph
– G2 is a complete directed graph
1
2 3
4 G1
G2

6. CHAPTER 6 6
Adjacent and Incident in
Undirected Graph
 If (v1, v2) is an edge in an undirected
graph
- v1 and v2 are adjacent
– The edge (v1, v2) is incident on
vertices v1 and v2
– Example In E(G), the vertices adjacent to
vertex 2 is 4,5 and 1
– The edges incident on vetex3 in E(G) are
(1,3), (3,6) and (3,7)

7. CHAPTER 6 7
Adjacent and Incident in
Directed Graph
 If <v0, v1> is an edge in a directed graph
– v0 is adjacent to v1, and v1 is adjacent from v0
– The edge <v0, v1> is incident on v0 and v1
– Example In E(G), <3, 2> - the vertex 3
is adjacent to vertex 2 where vertex 2 is
adjacent from vertex 3
– The edge <3, 2> is incident to 3 and 2.
E(G)

8. CHAPTER 6 8
0 2
1
(a)
3
2
1
4
(b)
self edge multigraph:
multiple occurrences
of the same edge
Figure 6.3
Multigraph is not a graph

9. CHAPTER 6 9
 A subgraph of G is a graph G’ such that V(G’) is a subset of V(G)
and E(G’) is a subset of E(G)
Subgraph
1
2 3
4
G1
G3

10. CHAPTER 6 10
 A simple path is a path in which all vertices
except possibly the first and last are distinct
 The length of a path is the number of edges on it
Path in Graph

11. CHAPTER 6 11
 A cycle is a simple path in which the first and
the last vertices are the same
Cycle in Graph
Cycle
Path

12. CHAPTER 6
12
 A connected component of an undirected graph
is a maximal connected subgraph.
 In an undirected graph G, two vertices, v0 and v1, are
connected if there is a path in G from v0 to v1
Connected Components

13. CHAPTER 6 13
 A strongly connected component is a maximal
subgraph that is strongly connected.
 A directed graph is strongly connected if there
is a directed path from vi to vj and also
from vj to vi.
Strongly Connected Component
G3

14. CHAPTER 6 14
0
1 2
3
0
1 2
3 4 5 6
G1
G2
Tree (acyclic graph)
A tree is a graph that is connected and acyclic
Acyclic Graph
Connected

15. CHAPTER 6 15
Degree
 The degree of a vertex is the number of edges
incident to that vertex
 For directed graph,
– in-degree of a vertex v is the number of
edges that have v as the head
– out-degree of a vertex v is the number of
edges that have v as the tail

16. CHAPTER 6
16
Degree in Undirected graph
0
1 2
3 4 5 6
G1 G2
3
2
3 3
1 1 1 1
0
1 2
3
33
3

17. CHAPTER 6 17
Degree

18. CHAPTER 6
18
Degree in Directed graph
Directed graph
in-degree
out-degree
G3
indegree:1
outdegree: 1
indegree: 1
outdegree: 2
indegree: 1
outdegree: 0

19. Quiz
 https://quizizz.com/admin/quiz/5f5de89ead
5020001dab5a3a
CHAPTER 6 19

20. CHAPTER 6 20
Graph Representations
 Adjacency Matrix
 Adjacency Lists
 Adjacency Multilists

21. CHAPTER 6 21
Adjacency Matrix
 Let G=(V,E) be a graph with n vertices.
 The adjacency matrix of G is a two-dimensional
n * n array, say A(i,j)
 If the edge (vi, vj) is in E(G), A(i,j) =1
 If there is no such edge in E(G), A(i,j) =0
 The adjacency matrix for an undirected graph is
symmetric; the adjacency matrix for a digraph
need not be symmetric

22. CHAPTER 6 22
Examples for Adjacency Matrix
0
1
1
1
1
0
1
1
1
1
0
1
1
1
1
0












0
1
0
1
0
0
0
1
0










0
1
1
0
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
1
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
1
0


























G1
G2
G4
1
2 3
4
1
2
3
2
1
3
4
5
6
7
8
symmetric
e is the No. of Edges
undirected:e<< n2/2
directed: e<n2

23.  The representation the n rows of the
adjacency matrix are represented as n linked
lists.
 There is one list for each vertex in G.
 Each node has at least two fields: VERTEX
and LINK
 The VERTEX fields contain the indices of
the vertices adjacent to vertex i.
CHAPTER 6 23
Adjacency Lists
Each row in adjacency matrix is represented as an adjacency list.

24. CHAPTER 6 24
Adjacency Lists- Undirected
Graph
The Adjacency lists for G1 is shown

25. CHAPTER 6 25
Adjacency Lists –Directed Graph
The Adjacency lists for G3 is shown

26. CHAPTER 6 26
Adjacency Lists- Connected
Components
The adjacency lists for G4 is shown

27. CHAPTER 6 27
Inverse Adjacency Lists
Inverse adjacency lists for G3
Each node would now have four fields and would represent one edge.
The node structure would be
tail head column link for head row link for tail

28. CHAPTER 6 28
Adjacency Multilists
An edge in an undirected graph is
represented by two nodes in adjacency list
representation.
Adjacency Multilists
–lists in which nodes may be shared among
several lists.
(an edge is shared by two different paths)

29. Adjacency Multilists
CHAPTER 6 29

30. Adjacency Multilists
CHAPTER 6 30
Adjacency List for G1

31. Adjacency Multilists
CHAPTER 6 31

32. CHAPTER 6 32
TRAVERSALS
 Traversal
Given G=(V,E) and vertex v, find all wV,
such that w connects v.
– Depth First Search (DFS)
preorder tree traversal
– Breadth First Search (BFS)
level order tree traversal
 Connected Components
 Spanning Trees

33. CHAPTER 6 33
Depth First Search (DFS)
If a depth first search is initiated from vertex v1,
then the vertices of G are visited in the
order: v1, v2, v4, v8, v5, v6, v3, v7.

34. CHAPTER 6 34
Breadth First Search (BFS)
A breadth first search beginning at vertex v1 of the graph.
First visit v1 and then v2 and v3. Next
vertices v4, v5, v6 and v7 will be visited and finally v8.

35. CHAPTER 6 35
Graph and its Adjacency List

36. CHAPTER 6 36
Connected Components

37. CHAPTER 6 37
Spanning Trees
 When graph G is connected, a depth first or
breadth first search starting at any vertex will
visit all vertices in G
 A spanning tree is any tree that consists solely
of edges in G and that includes all the vertices
 E(G): T (tree edges) + N (nontree edges)
where T: set of edges used during search
N: set of remaining edges

38. CHAPTER 6 38
Examples of Spanning Tree
G1 Possible spanning trees

39. CHAPTER 6 39
Spanning Trees
 Either DFS or BFS can be used to create a
spanning tree
– When DFS is used, the resulting spanning tree is
known as a depth first spanning tree
– When BFS is used, the resulting spanning tree is
known as a breadth first spanning tree
 While adding a nontree edge into any spanning
tree, this will create a cycle

40. CHAPTER 6 40
DFS VS BFS Spanning Tree
DFS Spanning BFS Spanning

41. CHAPTER 6 41
Minimum Cost Spanning Tree
 The cost of a spanning tree of a weighted
undirected graph is the sum of the costs of the
edges in the spanning tree
 A minimum cost spanning tree is a spanning
tree of least cost
 Three different algorithms can be used
– Kruskal
– Prim
– Sollin
Select n-1 edges from a weighted graph
of n vertices with minimum cost.

42. Minimum Cost Spanning Tree
CHAPTER 6 42

43. Kruskal’s Algorithm
CHAPTER 6 43

44. Kruskal’s Algorithm
CHAPTER 6 44

45. SHORTEST PATHS AND TRANSITIVE
CLOSURE
 Single Source All Destinations
CHAPTER 6 45

46. Analysis of Algorithm SHORTEST PATH
CHAPTER 6 46

47. Analysis of Algorithm SHORTEST PATH
CHAPTER 6 47

48. CHAPTER 6 48

49. All Pairs Shortest Paths
 Ak(i,j) = min {Ak-1(i,j), Ak-1(i,k) + Ak -1(K,j)}
K>=1 and
 Ao(i,j) = COST(i,j)
CHAPTER 6 49

50. All Pairs Shortest Paths
CHAPTER 6 50

51. Cost Matrix
CHAPTER 6 51

52. Transitive Closure
CHAPTER 6 52
Figure 6.25 Graph G and Its Adjacency
Matrix A, A+ and A*
A+(i,j) = 1 if path length >0
A*(i,j) = 1 if path length >=0