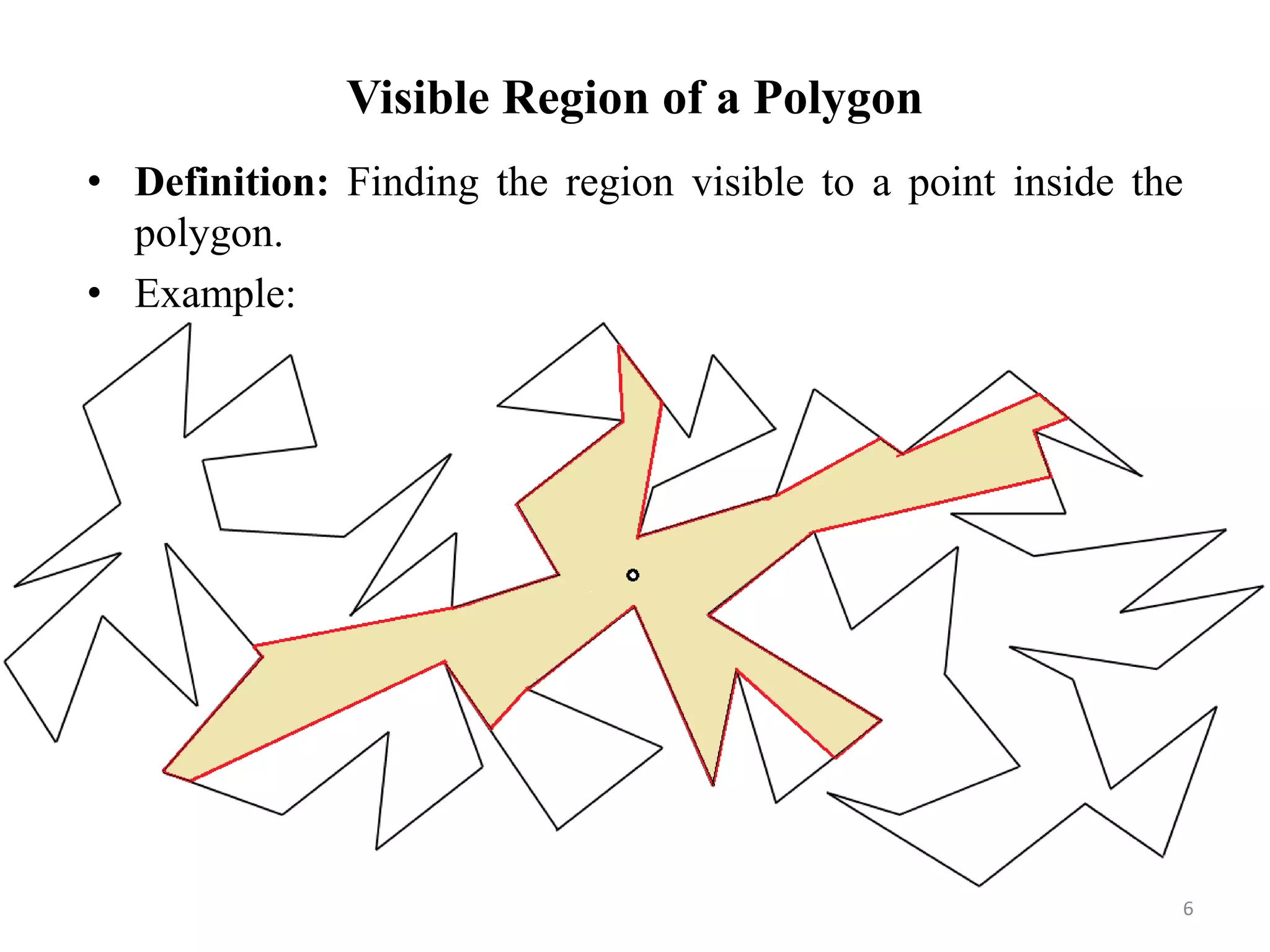
The document presents an algorithm to find the visible region of a polygon in O(n^2) time and O(n) space. It first finds the visible vertices region by checking each vertex for intersections with edges in O(n^2) time. It then extends this region to the full visible region by considering gaps between visible vertices and finding intersection points of extreme lines in O(n) time. The algorithm avoids issues with existing approaches and produces the exact visible region without unnecessary points.

1. An Algorithm to Find the Visible Region
of a Polygon
Kasun Ranga Wijeweera
(krw19870829@gmail.com)
1

2. Introduction
2

3. What is a Polygon?
• Let v0, v1, v2…, vn-1 be n points in the plane.
• Let e0 = v0v1, e1 = v1v2…, ei = vivi+1…, en-1 = vn-1v0 be n
segments connecting the points.
• These segments bound a polygon if and only if
1. The intersection of each pair of segments adjacent in the
cyclic ordering is the single point shared between them: ei ∩
ei+1 = vi+1, for all i = 0…, n – 1.
2. Nonadjacent segments do not intersect: ei ∩ ej = Ф, for all j
≠ i + 1.
3. None of three consecutive vertices are collinear.
Note that all index arithmetic are modulo n.
3

4. Examples of Polygons
4

5. Examples of Polygons…
5

6. Visible Region of a Polygon
• Definition: Finding the region visible to a point inside the
polygon.
• Example:
6

7. Research Problem
• The naïve algorithm to find the visible region inside a
polygon takes O (k * n) time and O (n) space where k is the
number of rays shot around the point.
• The output of this algorithm may contain lots of unnecessary
collinear points.
• The other existing algorithms are extremely complicated and
far from reality to provide correct implementations to them.
• An algorithm is proposed to find the visible region of a
polygon in O (n2) time and O (n) space.
• The proposed algorithm can find the exact visible region and
it does not produce unnecessary collinear points.
7

8. Literature Survey
8

9. Visible Region Algorithms
• Naïve approach: O (k * n)
• Suri et al. (1986): O (n log n)
• Asano et al. (1986): O (n log n)
• Joe & Simpson (1987) : O (n)
• Vegter (1990): O (k log (n/k))
• Aronov et al. (2002): O (log2 n + k)
• Zarei & Ghodsi (2005): O (1 + min (h, k) log n + k)
• Heffernan & Mitchell (2006): O (n + h log h), h holes
• Francisc et al. (2014): O (n)
9

10. Methodology
10

11. Research Paper
K. R. Wijeweera, S. R. Kodituwakku (2015), An Algorithm to
Find the Visible Region of a Polygon, Ceylon Journal of
Science (Physical Sciences), Volume 19, pp. 33 - 44.
11

12. Visible Region of a Polygon Example
12

13. Representation of the Polygon
• The variable points stores the number of vertices of the
polygon.
• The coordinates of the vertices of the polygon are stored
using two arrays x and y.
• Then (x[i], y[i]) denotes the ith vertex of the polygon where i
= 0, 1…, (points - 1).
13

14. Intersection of Two Line Segments
• Suppose L1 and L2 are two line segments.
• End points of L1 are P1 (x1, y1) and P2 (x2, y2).
• End points of L2 are P3 (x3, y3) and P4 (x4, y4).
• The function isIntersect returns 1 if these line segments x-
intersect else returns 0.
14
✔ ✘ ✘

15. Intersection of Two Line Segments…
• The visible region is computed with respect to the given point
(xp, yp).
• The function isIntersect has two parameters v and i.
• Here j = (i + 1) MODULO points.
15

16. Intersection of Two Line Segments…
• If following two conditions are satisfied only then L1 and L2
x-intersect.
1. P3 and P4 should be in two sides of L1.
2. P1 and P2 should be in two sides of L2.
16
✔ ✘ ✘

17. Intersection of Two Line Segments…
• The function isTwoSides {P1, P2, P3, P4} returns 1 if points P3
and P4 are situated in opposite sides of the line P1P2 else the
function returns 0.
• Therefore, isTwoSides {P1, P2, P3, P4} && isTwoSides {P3,
P4, P1, P2} = 1  the two line segments x-intersect.
17

18. Test for X-Intersection
• The vertices of the triangle: P1 (x1, y1), P2 (x2, y2), P3 (x3, y3).
• Let t = x1 * (y2 – y3) + x2 * (y3 – y1) + x3 * (y1 – y2).
• t = 0 ↔ (P1, P2, P3) are collinear.
• t > 0 ↔ (P1, P2, P3) are in anticlockwise order.
• t < 0 ↔ (P1, P2, P3) are in clockwise order.
• The function tv returns the sign of value t.
18
t > 0 t < 0

19. Test for X-Intersection…
• If tv{P1, P2, P3} * tv{P1, P2, P4} < 0  P3, P4 are on same
side of L.
• If tv{P1, P2, P3} * tv{P1, P2, P4} > 0  P3, P4 are on opposite
sides of L.
19

20. Finding the Visible Vertices
• The visibility is decided with respect to point P which is
inside the polygon.
• A vertex is said to be visible to the point P, if the line segment
joining the point P and the vertex does not have any x-
intersections with the edges of the polygon.
• The function checkVisible is used.
• The array vs stores the indices of visible vertices.
• The variable pvs stores the number of visible vertices.
• If there is at least one x-intersection then vertex is not visible.
(Use of keyword BREAK)
20

21. Finding the Visible Vertices…
• Following figure shows the ‘visible vertices region’.
• This region is a sub region of visible region.
21

22. Visible Vertices Region to Visible Region
• The function createRegion extends the visible vertices region
to visible region.
• The visible region is stored using arrays xv and yv where
(xv[i], yv[i]) denotes the ith vertex of the visible region.
• The variable pt stores the number of vertices of the visible
region.
• The variable gap stores the number of edges between two
consecutive visible vertices.
• Each visible vertex is accessed: FOR (i = 0 TO (pvs - 1))
{…}.
• Then gap = vs[j] – vs[i] where j = (i + 1) MODULO pvs.
• If gap < 0 then gap = gap + points.
• Initially pt = 0 then xv[pt] = x[vs[i]]; yv[pt] = y[vs[i]]; pt = pt
+ 1;.
22

23. Visible Vertices Region to Visible Region…
• Following figure shows the expanded region.
• If gap = 1 then no new points will be included.
• If gap > 0 then zero or more new points will be included
depending on the situation.
23

24. Two Important Results
• Two lines can be drawn by joining point P and each end point
of the gap.
• These two extreme lines form a region which is visible to the
point P.
• Number of new points required may vary depending on the
situation.
24

25. Two Important Results…
• Lemma 1: The number of new points for given gap cannot
exceed two.
• Lemma 2: If there are two new points for a given gap then
both of the new points should lie on the same edge of the
polygon.
25

26. The Function findIntersection
• Any two straight lines intersect unless they are parallel.
• Let’s consider two lines L1 and L2 formed by end points {P1
(x1, y1), P2 (x2, y2)} and {P3 (x3, y3), P4 (x4, y4)} respectively.
• If L1 and L2 are not parallel then these eight coordinates are
sent to function findIntersection to compute the intersection
point (xn, yn).
26

27. The Function findIntersection…
• Let’s take (m1, c1) and (m2, c2) as the (gradient, y-intercept)
of each line respectively if they exist.
• There are four different cases of these two lines.
27

28. The Function findIntersection …
• Case 1; (x1 = x2; x3 = x4): This case is ignored and not
handled using the function. Only coordinates of non-parallel
lines are sent to the function.
28

29. The Function findIntersection…
• Case 2; (x1 = x2; x3 ≠ x4): L1 is parallel to y-axis and L2 is
not parallel to y-axis.
• m2 = (y3 – y4)/(x3 – x4);
• c2 = y3 – m2 * x3;
• xn = x1;
• yn = m2 * xn + c2;
29

30. The Function findIntersection…
• Case 3; (x1 ≠ x2; x3 = x4): L1 is not parallel to y-axis and L2
is parallel to y-axis.
• m1 = (y1 – y2)/(x1 – x2);
• c1 = y1 – m1 * x1;
• xn = x3;
• yn = m1 * xn + c1;
30

31. The Function findIntersection…
• Case 4; (x1 ≠ x2; x3 ≠ x4): Both L1 and L2 are not parallel to
y-axis.
• m1 * xn + c1 = m2 * xn + c2  xn = (c2 – c1)/(m1 – m2);
• yn = m1 * xn + c1;
31

32. An Illustrative Example
• ABV1V2 is the visible vertices region with respect to the
point P.
• There is a gap between vertices V1 and V2.
• Let E1 and E2 be the two extreme lines drawn through
vertices V1 and V2 respectively.
32

33. An Illustrative Example…
• Again let’s look at function createRegion.
• If gap > 1 then found = 0.
• Each edge within the gap is accessed.
• The variables f and g store the indices of each vertex of an
edge.
• V1 ≡ (x[vs[i]], y[vs[i]]) and V2 ≡ (x[vs[j]], y[vs[j]]).
• First, the extreme line E1 is considered where E1 = VP1.
• The function isTwoSides is used to find edges which x-
intersect E1.
• The function findIntersection is used to compute the
intersection points.
• The function setClosest is used to select the actual insertion
point out of those intersection points.
33

34. An Illustrative Example…
• Being found = 1 means that the line E1 generates a new point.
• If found = 1 then xv[pt] = xg; yv[pt] = yg; pt = pt + 1.
• If line E2 generates a new point then it should generate it with
the same edge for E1. (The Trick)
• The functions isTwoSides and findIntersection are used for
line E2 as well.
• Then xv[pt] = xn; yv[pt] = yn; pt = pt + 1;.
34

35. An Illustrative Example…
• Being still found = 0 means that the line E1 does not generate
any new points.
• However, the line E2 may generate a new point.
• Then the functions isTwoSides, findIntersection and
setClosest are used for line E2.
• If found = 1 then xv[pt] = xg; yv[pt] = yg; pt = pt + 1;.
35

36. A Trick to Save Computational Cost
• This result is derived from Lemma 2.
• Result: If one extreme line causes to have a new intersection
point intersecting with a particular edge. Then the other
extreme line either does not cause any new insertion points or
makes a new insertion point with the same edge.
36

37. The Function setClosest
• The purpose of this function is to find the actual insertion
point among a set of candidate insertion points.
• The variables dx and dy are used to store the projections on x
and y axes respectively.
• The function ab returns the absolute value of its argument.
• The projection with maximum magnitude is selected in order
to avoid precision error.
37

38. The Function setClosest
• Here, dx = x[i] - xp.
• Then, dx * (xn - xp) > 0 if and only if lines x = xn and x =
x[i] are on the same side of the line x = xp.
• Therefore, intersection points I4 and I5 can be rejected.
• Now, the closest point to the point P among of I1, I2, and I3 is
selected.
• Similar approach is used if the projection is on y-axis.
38

39. Back to Previous Example
• The visible vertices region can be extended to visible region
for the following example as explained.
• Note that visible region of this particular example is a
polygon.
39

40. Visible Region is not Necessarily be a Polygon
• The term “visible region” is used instead “visible polygon”.
• Suppose points P, B, C, and D are collinear.
• Then the visible region with respect to the point P is {A, B,
C, D, E}.
• Edges BC and CD touch more than from a single point.
• Therefore, visible region is not a polygon.
40

41. Results and Discussion
41

42. Time Complexity
• Let n be the number of vertices in the given polygon.
• It takes O (n) time to test whether a given vertex is visible by
checking intersection with each edge.
• Therefore, it takes n * O (n) = O (n2) time to find the visible
vertices region.
42

43. Time Complexity…
• In the worst case, the visible vertices region has a single gap
with (n - 2) edges.
• One of the extreme lines should be tested against each edge
within the gap in order to find intersection edge and it takes
O (n) time.
• Processing the other extreme line takes only O (1) time.
• Therefore, it takes O (n) + O (1) = O (n) time to extend
visible vertices region to visible region.
• Thus, the time complexity of the proposed algorithm is O (n2)
+ O (n) = O (n2).
43

44. Space Complexity
• It takes n memory cells to hold x-coordinates and n memory
cells to hold y-coordinates.
• Altogether, it takes 2n memory cells to hold the input.
• Therefore, it needs O (n) space to hold the input.
• The memory needed for workspace is O (1).
• Therefore, the space complexity of the proposed algorithm is
O (n) + O (n) + O (1) = O (n).
44

45. Comparison
• The naïve algorithm takes O (k * n) time and O (n) space
where k is the number of rays shot around the point.
• The efficiency of the naïve algorithm is sufficiently enough
for many applications such as video games.
• In order to get a sufficiently accurate output, k should be
larger than n.
• The output of the naïve algorithm contains lots of
unnecessary collinear points.
• There are number of theoretical algorithms available in
literature.
• However, they are extremely complicated and far from reality
to provide a computer implementation.
• The proposed algorithm is faster than the naïve approach and
it does not produce unnecessary collinear points. 45

46. Conclusions
46

47. Conclusion
• The proposed visible region algorithm is faster than the naïve
algorithm and does not produce unnecessary collinear points.
47

48. Thank you!
48