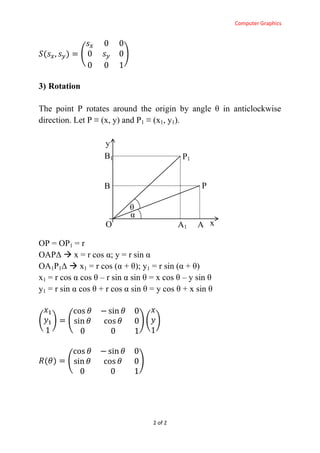
This document discusses 2D geometric transformations including translation, scaling, and rotation. Translation moves an object by adding offsets tx and ty to the x and y coordinates. Scaling enlarges or shrinks an object by multiplying the x and y coordinates by scaling factors sx and sy. Rotation rotates an object around the origin by an angle θ, with the new x and y coordinates calculated using trigonometric functions of the original point coordinates and θ.

1. Computer Graphics
1 of 2
Lesson 4: 2D Geometric Transformations I
Author: Kasun Ranga Wijeweera
Email: krw19870829@gmail.com
Date: 2020 August 16
Types of Transformations
1) Translation
2) Scaling
3) Rotation
1) Translation
Let P ≡ (x, y) and P1 ≡ (x1, y1) such that x1 = x + tx and y1 = y + ty.
( ) ( ) ( )
( ) ( )
2) Scaling
Let P ≡ (x, y) and P1 ≡ (x1, y1) such that x1 = sxx and y1 = syy.
( ) ( ) ( )

2. Computer Graphics
2 of 2
( )
3) Rotation
The point P rotates around the origin by angle θ in anticlockwise
direction. Let P ≡ (x, y) and P1 ≡ (x1, y1).
OP = OP1 = r
OAPΔ  x = r cos α; y = r sin α
OA1P1Δ  x1 = r cos (α + θ); y1 = r sin (α + θ)
x1 = r cos α cos θ – r sin α sin θ = x cos θ – y sin θ
y1 = r sin α cos θ + r cos α sin θ = y cos θ + x sin θ
( ) ( ) ( )
( )
O x
y
P
P1
AA1
B
B1
α
θ