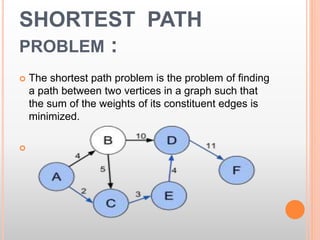
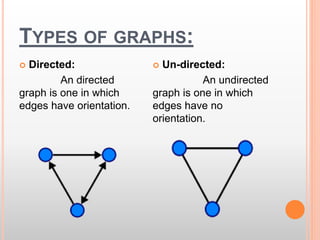
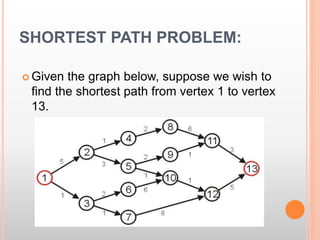
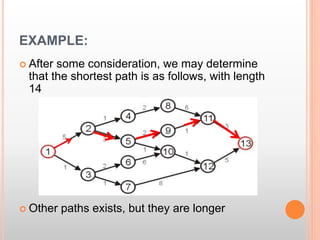
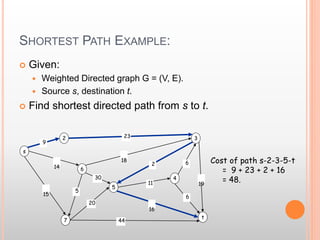
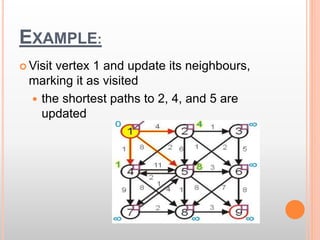
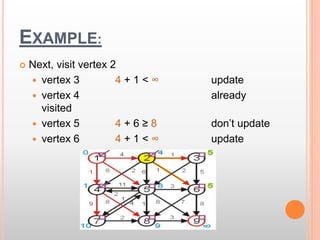
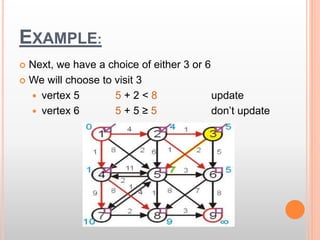
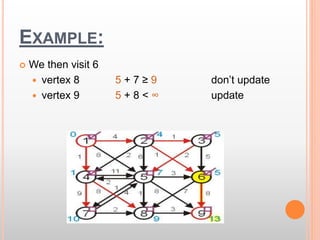
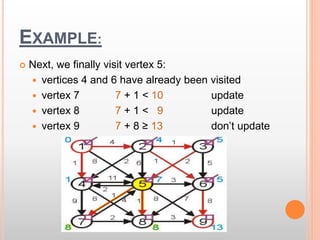
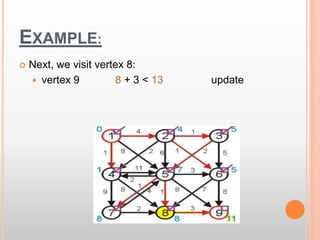
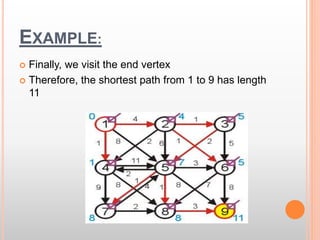
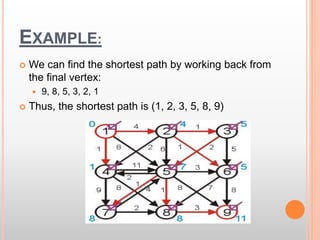
This document presents information about the shortest path problem in graphs. It defines key graph terms like vertices, edges, and discusses weighted, directed, and undirected graphs. It provides an example of finding the shortest path between two vertices in a graph using Dijkstra's algorithm and walks through the steps of running the algorithm on a sample graph to find the shortest path between vertices 1 and 9.