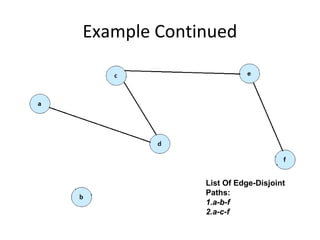
The document outlines an algorithm to find all edge-disjoint paths between a source and target in a graph, utilizing Dijkstra's shortest-path algorithm. It includes pseudo-code for the algorithm, which counts the disjoint paths by repeatedly finding and deleting paths until none remain. The algorithm is applicable to both unweighted and weighted graphs, and can be modified to work for vertex-disjoint paths as well.

1. Algorithm To Count Number of
Disjoint Paths Between A Source
and Target, In A Given Graph
Sujith Nair

2. Introduction
• This algorithm finds all the edge-disjoint paths
between a source S ∈ V and a target T ∈ V, in a
given graph G(E,V).
• The algorithm uses Dijkstra’s Single-Source-
Shortest-Path algorithm as a sub-routine.

3. Pseudo-Code
disjoint-path(G[n][n],X,Y){
path=path_find(X,Y);
while(path!=NULL){
count++;
delete_path(G,path);
path=path_find(X,Y);
}
return count;
}

4. delete_path(G,path){
for each edge in path
G:=G-edge;
}

5. path_find(G,X,Y){
for each vertex V in G:
dist[v]:=infinity;
previous[v]:= undefined;
dist[x]:=0;
Q:= set of all nodes in G;
while Q is not empty
u:=vertex in Q with smallest distance in
dist[];

6. If dist[u]=infinity:
break;
remove u from Q;
for each neighbour v of u:
alt:= dist[u]+1;
if alt<dist[v]:
dist[v]:=alt;
previous[v]=u;

7. path:=empty sequence;
k=Y;
while (previous[k]!=NULL)
insert k at the end of path;
k:=previous[k];
return path;
}

8. Example
Source Vertex: a
Target Vertex: f

9. Example Continued.
List Of Edge-
Disjoint Paths:
1. a-b-f

10. Example Continued
List Of Edge-Disjoint
Paths:
1.a-b-f
2.a-c-f

11. Example Continued
List Of Edge-
Disjoint Paths:
1.a-b-f
2.a-c-f
3.a-d-c-f

12. Endnotes
• This algorithm will also work in the case of
weighted graphs. In the case of weighted
graphs, the algorithm returns a list of paths
with the lowest weights.
• This algorithm, with minor modifications, will
also work for the case of vertex-disjoint paths.

13. Thank You