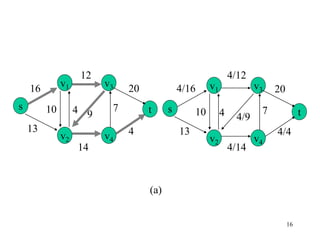
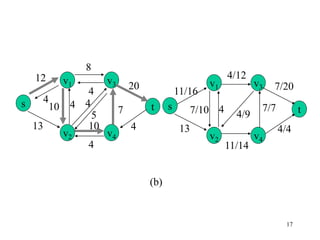
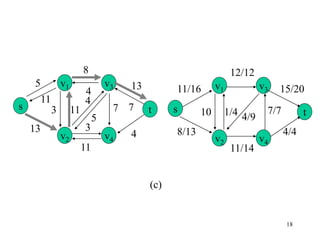
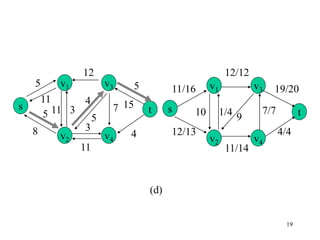
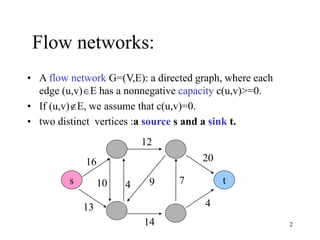
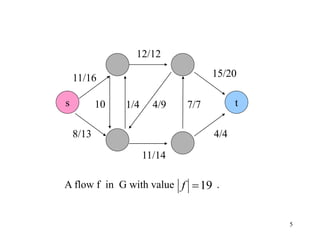
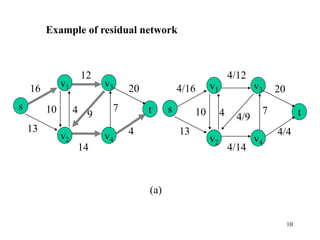
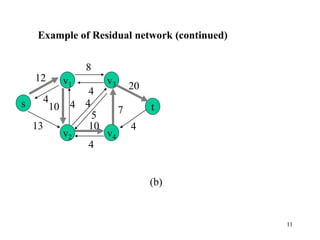
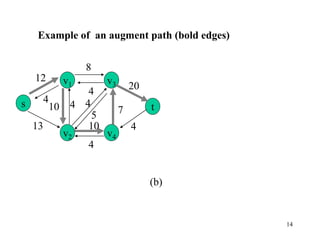
This document describes the maximum flow problem and the Ford-Fulkerson algorithm for finding the maximum flow in a flow network. It defines flow networks as directed graphs with edge capacities and discusses the concepts of flow, residual networks, augmenting paths, and how the Ford-Fulkerson method works by repeatedly finding augmenting paths and pushing additional flow along these paths until no more are possible. The time complexity of the basic Ford-Fulkerson algorithm is O(|E|f*) where |E| is the number of edges and f* is the value of the maximum flow.

1. Maximum Flow
Prepared by
Md. Shafiuzzaman
Lecturer, Dept. of CSE. JUST

2. 2
Flow networks:
• A flow network G=(V,E): a directed graph, where each
edge (u,v)E has a nonnegative capacity c(u,v)>=0.
• If (u,v)E, we assume that c(u,v)=0.
• two distinct vertices :a source s and a sink t.
s t
16
12
20
10 4 9 7
413
14

3. 3
Flow:
• G=(V,E): a flow network with capacity function c.
• s-- the source and t-- the sink.
• A flow in G: a real-valued function f:V*V  R satisfying
the following two properties:
• Capacity constraint: For all u,v V,
we require f(u,v)  c( u,v).
• Flow conservation: For all u V-{s,t}, we require
 
vine voute
efef
.. ..
)()(

4. 4
Net flow and value of a flow f:
• The quantity f (u,v) is called the net flow from
vertex u to vertex v.
• The value of a flow is defined as
– The total flow from source to any other vertices.
– The same as the total flow from any vertices to
the sink.


Vv
vsff ),(

5. 5
s t
11/16
12/12
15/20
10 1/4 4/9 7/7
4/48/13
11/14
A flow f in G with value .19f

6. 6
Maximum-flow problem:
• Given a flow network G with source s and sink t
• Find a flow of maximum value from s to t.
• How to solve it efficiently?

7. 7
The Ford-Fulkerson method
• We call it a “method” rather than an “algorithm” because
it encompasses several implementations with different
running times.
• The Ford-Fulkerson method depends on three important
ideas that transcend the method and are relevant to many
flow algorithms and problems:
– residual networks,
– augmenting paths,
– and cuts.

8. 8
Continue:
• FORD-FULKERSON-METHOD(G,s,t)
• initialize flow f to 0
• while there exists an augmenting path p
• do augment flow f along p
• return f

9. 9
Residual networks:
• Given a flow network and a flow, the residual
network consists of edges that can admit more net
flow.
• G=(V,E) --a flow network with source s and sink t
• f: a flow in G.
• The amount of additional net flow from u to v
before exceeding the capacity c(u,v) is the residual
capacity of (u,v), given by: cf(u,v)=c(u,v)-f(u,v)
in the other direction: cf(v, u)=c(v, u)+f(u, v).

10. 10
s
20
7
9
v2 v4
t
v3v116
13
12
10 4
4
14
4/9
s
v2 v4
t
v3v14/16
13
4/12
10 4
20
4/4
7
4/14
(a)
Example of residual network

11. 11
5
s
v2 v4
t
v3v1
12
13
8
10 4
20
4
7
4
4
4
4
10
(b)
Example of Residual network (continued)

12. 12
Fact 1:
• Let G=(V,E) be a flow network with source s and sink t,
and let f be a flow in G.
• Let Gf be the residual network of G induced by f,and let f’
be a flow in Gf.Then, the flow sum f+f’ is a flow in G with
value .
• f+f’: the flow in the same direction will be added.
the flow in different directions will be cnacelled.
'' ffff 

13. 13
Augmenting paths:
• Given a flow network G=(V,E) and a flow f, an
augmenting path is a simple path from s to t in the residual
network Gf.
• Residual capacity of p : the maximum amount of net flow
that we can ship along the edges of an augmenting path p,
i.e., cf(p)=min{cf(u,v):(u,v) is on p}.
2 3 1
The residual capacity is 1.

14. 14
5
s
v2 v4
t
v3v1
12
13
8
10 4
20
4
7
4
4
4
4
10
(b)
Example of an augment path (bold edges)

15. 15
The basic Ford-Fulkerson
algorithm:
FORD-FULKERSON(G,s,t)
1. for each edge (u,v)E[G]
2. do f[u,v] 0
3. f[v,u] 0
4. while there exists a path p from s to t in the residual network
Gf
5. do cf(p) min{cf(u,v): (u,v) is in p}
6. for each edge (u,v) in p
7. do f[u,v] f[u,v]+cf(p)
8.





16. 16
s
20
7
9
v2 v4
t
v3v116
13
12
10 4
4
14
4/9
s
v2 v4
t
v3v14/16
13
4/12
10 4
20
4/4
7
4/14
(a)

17. 17
5
s
v2 v4
t
v3v1
12
13
8
10 4
20
4
7
4
4
4
4
10
4/9
s
v2 v4
t
v3v1
11/16
13
4/12
7/10 4
7/20
4/4
7/7
11/14
(b)

18. 18
5
s
v2 v4
t
v3v15
13
8
3 11
4
7
11
11
4
4
3
13
7
4/9
s
v2 v4
t
v3v111/16
8/13
12/12
10 1/4
15/20
4/4
7/7
11/14
(c)

19. 19
5
s
v2 v4
t
v3v15
8
11 3
4
7
11
11
12
4
3
5
15
5 9
s
v2 v4
t
v3v111/16
12/13
12/12
10 1/4
19/20
4/4
7/7
11/14
(d)

20. 20
s
v2 v4
t
v3v15
12
12
11 3
1
4
11
9
3
1
197
(e)

21. 21
Time complexity:
• If each c(e) is an integer, then time complexity is O(|E|f*),
where f* is the maximum flow.
• Reason: each time the flow is increased by at least one.
• This might not be a polynomial time algorithm since f* can
be represented by log (f*) bits. So, the input size might be
log(f*).