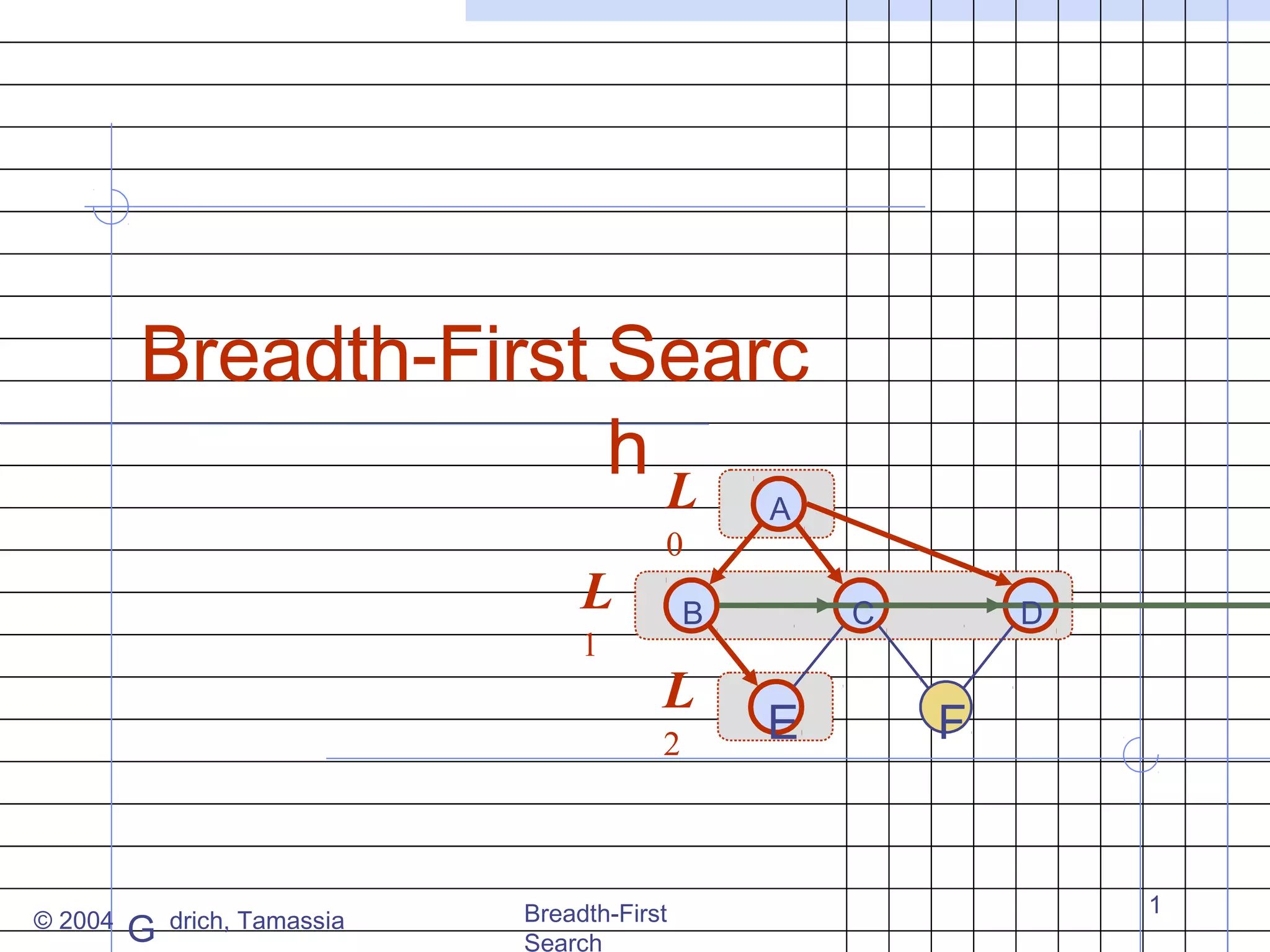
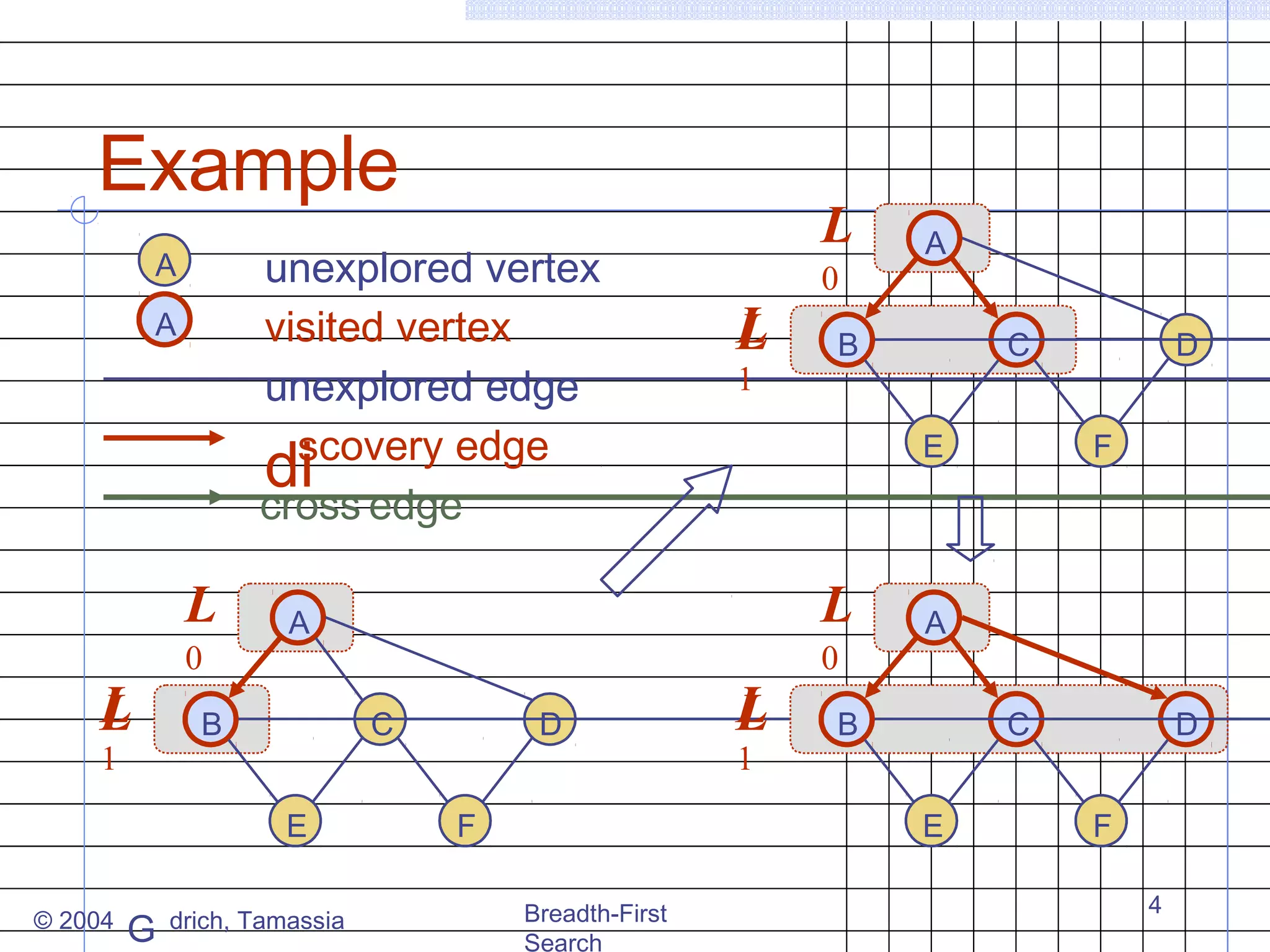
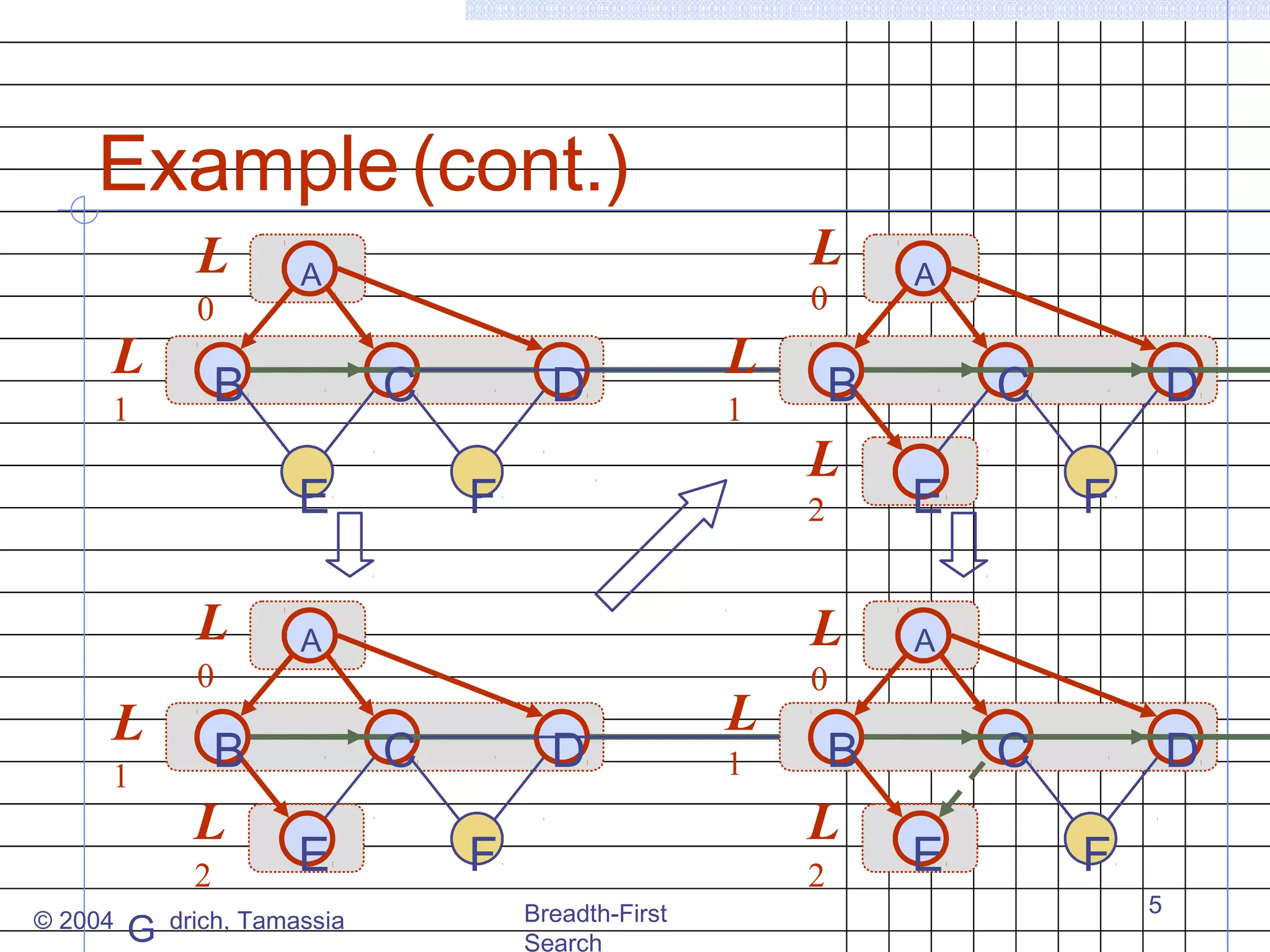
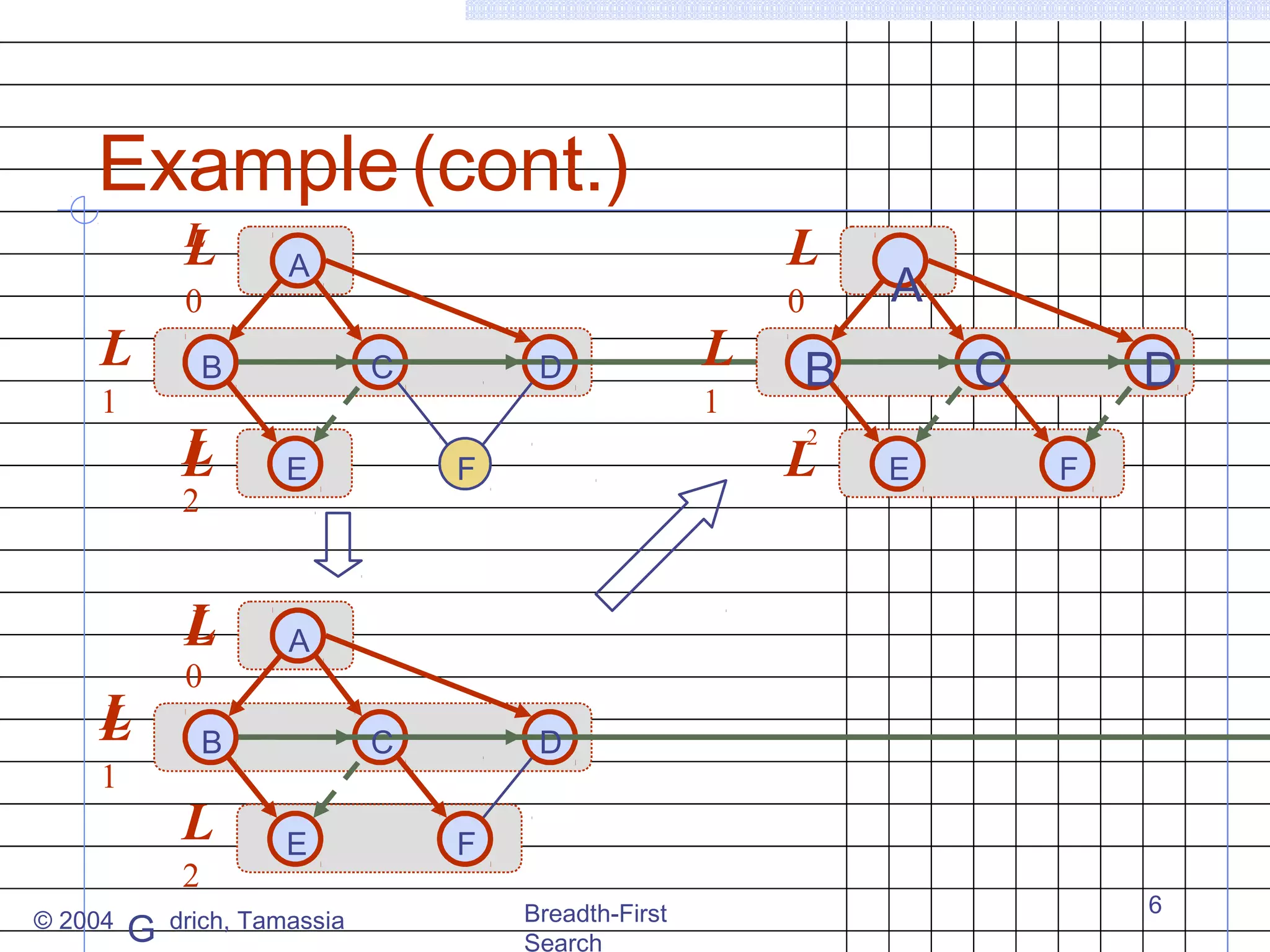
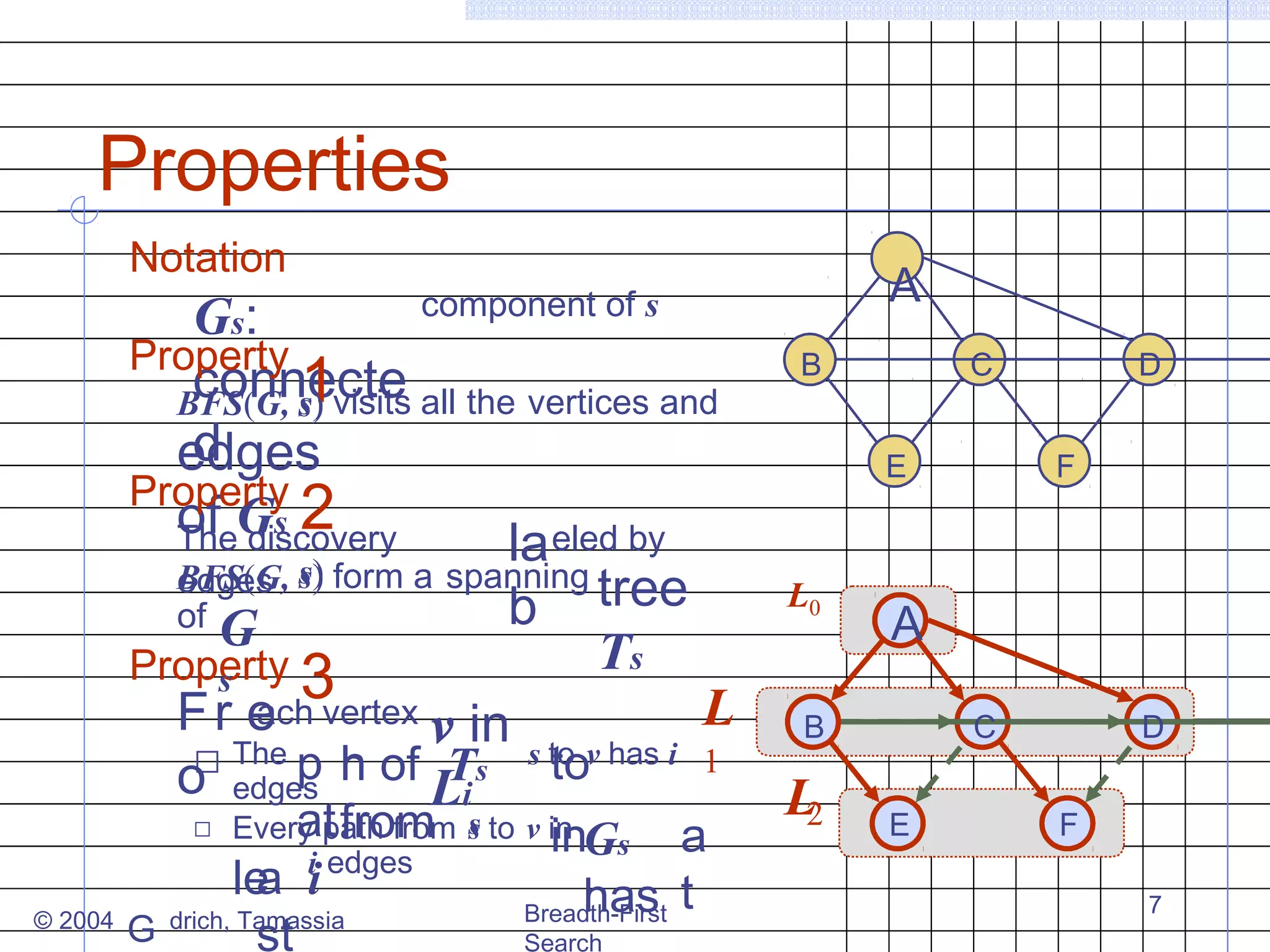
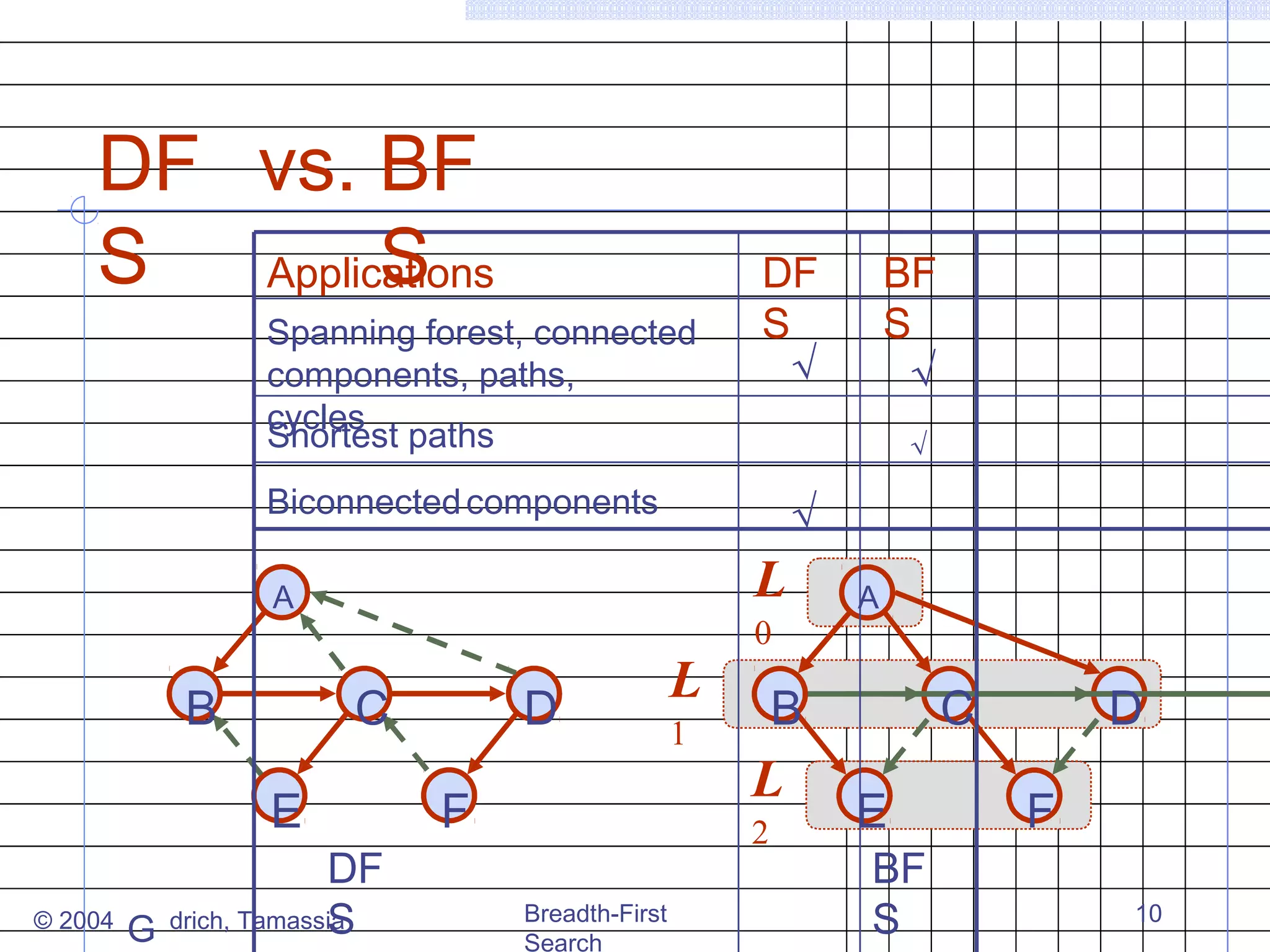
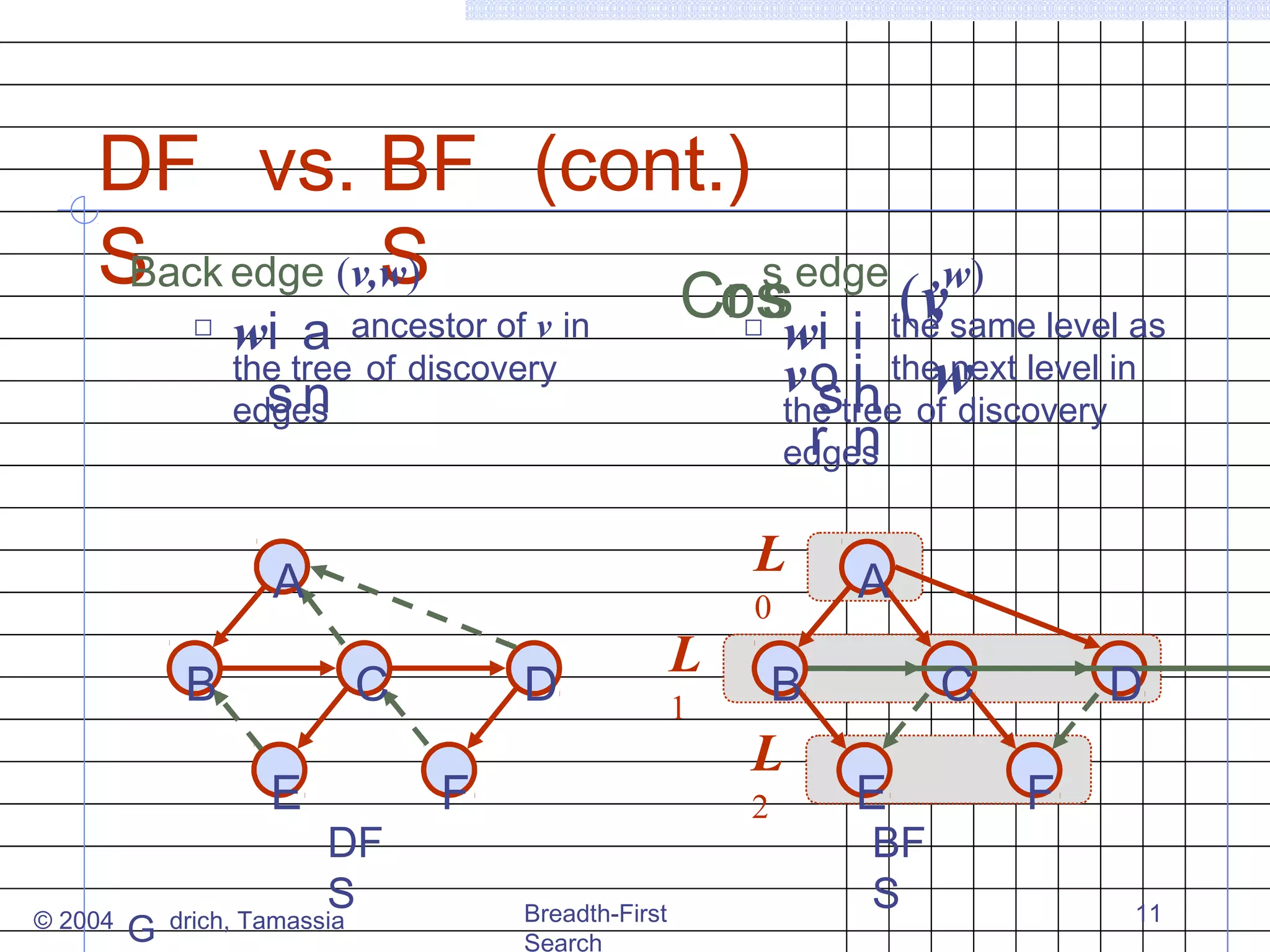
Breadth-first search (BFS) is an algorithm for traversing or searching trees or graphs. It begins at a root node and explores all neighboring nodes at the present depth prior to moving on to the nodes at the next depth level. The key properties of BFS are that it visits all vertices and edges, computes connected components, and finds the shortest path between any two vertices in terms of the number of edges. BFS runs in O(n+m) time on a graph with n vertices and m edges.

1. Breadth-First Searc
hL
L
1
0
B
L
2
© 2004
G
drich, Tamassia
A
Breadth-First
Search
C
E
D
F
1

2. Breadth-First Searc (§ 12.3.3)
Breadth-first search h
BF on a graph ith n
w
(BFS) is a general
nique for traversing
te
ch
a graph
ABF traversal o a
graph G
S
f
v rtices and
edges of G
e
„ Determines whether G is
„ Visits all the
connected
„ Computes the connected
components of G
„ Computes a spanning
forest of G
© 2004
G
drich, Tamassia
Breadth-First
Search
vertices and m edges
S
ta s O(n + m ) time
ke
s
BF can be further
extended to solve other
S
graph problems
Find and report a p t
with the minimum
number of edges a h
between two given
vertices
„ Find a simple cycle, if
there is one
„
2

3. BF Algorithm
The algorithm uses a
S mechanism for setting and
getting “labels” of vertices
of
and edges
Algorithm BFS(G)
Input graph G
Output labeling of the edges
and partition of the
vertices of G
for all u ∈
G.ertce()
setLabel(u, UNEXPLORED)
for all e ∈ G.edges()
∈ v i s
setLabel(e, UNEXPLORED)
for all v ∈ G.vertices()
∈
if getLabel(v) = UNEXPLORED
BFS(G, v)
© 2004
G
drich, Tamassia
Algorithm BFS(G, s)
L
L0 ← new empty
L0.insertL )
bel(s, VISITED
sequence
se 0 be(s
tLa
i←
ast(s)
l
while ,new empty sequence
←
Lii.isEmpty()
for
¬L all v ∈∈
i
+1
Breadth-First
Search
for all e ∈ G.incidentEdges(v)
if Li.elements
getLabel(e)
=
← opposite(v,e)
()
w←
UNEXPLO
if getLabel(w) =
setLabel(e, DISCOVERY)
RED
setLabel(w, VISITED)
w, UNEXPLO
Li
RED
Li
else
setLabel(e, CROSS
+1.insertLas )
e,
i ← i +1
i
t(w)
3

4. Example
unexplored vertex
visited vertex
unexplored edge
scovery edge
di
cross edge
A
A
L
L
1
0
G
L
1
B
B
L
C
drich, Tamassia
0
D
F
A
C
E
A
E
© 2004
L
L
1
0
F
A
B
C
E
Breadth-First
Search
D
D
F
4

5. Example (cont.)
L
L
0
B
1
L
A
0
C
E
L
L
1
0
2
© 2004
G
L
F
drich, Tamassia
C
2
D
L
E
L
C
E
B
1
A
B
L
D
L
A
A
0
B
1
L
F
2
Breadth-First
Search
D
F
C
E
D
F
5

6. Example (cont.)
L
L
L
1
0
B
C
L
L
E
L
1
0
B
L
2
© 2004
G
D
L
1
0
A
B
C
D
A
2
L
L
A
drich, Tamassia
L
F
C
E
2
E
F
D
F
Breadth-First
Search
6

7. Properties
Notation
G s:
Property
B
connecte all the vertices and
1
BFS(G, s) visits
d
edges
Property
of Gs 2
The discovery
la eled by
BFS(G, s) form a spanning tree
edges
L0
b
of G
Ts
Property 3
s
ach
L B
F r e vertex v in
„ The p h of Ts s to v has i 1
to
o edges
Li
L
2
at from
Every path from s to v in
„
le ii edges
a
© 2004
G drich, Tamassia
st
component of s
inGs a
has t
Breadth-First
Search
A
C
E
D
F
A
C
E
D
F
7

8. Analysi
s Setting/getting a vertex/edge
Each vertex is labeled twice
label takes O(1) time
O
a UNEXPLORE
aD
s VISITED
Each edge is
s UNEXPLOREtwice
labeled
„ once
aD
once
a DISCOVERYoor
s CROSS
Each vertex is inserted once into a sequen
s
r is called
Method incidentEdges
for each vertex
„ once
„ once
„
once
BFS
the Li
O + m) time providedce graph
i O the adjacency list structure
( +
represented by
runs
„
© 2004
G
n that Σv
n
Recall
deg(v) = 2m
drich, Tamassia
Breadth-First
Search
i
s
8

9. Applications
Using the template method pattern, we can
specialize the BFS traversal of a
G to
solve
graphthe following problems in O(n + m) time
„ Compute the connected components of G
„
„
„
Compute a spanning forest of G
Find a simple cycle in G, or report that G is a
forest
Given two vertices of G, find a path in G between
G number edges, or
them wi the mi
nimum
t
o
report that no such path exists
h
© 2004
G
drich, Tamassia
f
Breadth-First
Search
9

10. DF vs. BF
S
S
Applications
Spanning forest, connected
components, paths,
cycles
Shortest paths
DF
S
√
√
L
A
C
E
© 2004
DF
S
G drich, Tamassia
D
F
L
1
0
A
B
L
2
Breadth-First
Search
√
√
Biconnected components
B
BF
S
C
E
BF
S
D
F
10

11. DF vs. BF (cont.)
S edge (v,w)
S
Back
s edge ,w)
Cr swi i the, same level as
os
(v
ancestor of v in
wi a
„
„
next
vo n thew level in
i
s
the tree of discovery
r n
edges
the tree of discovery
sn
edges
L
A
B
C
E
© 2004
G
DF
S
drich, Tamassia
D
F
L
1
0
B
L
2
Breadth-First
Search
A
C
E
BF
S
D
F
11