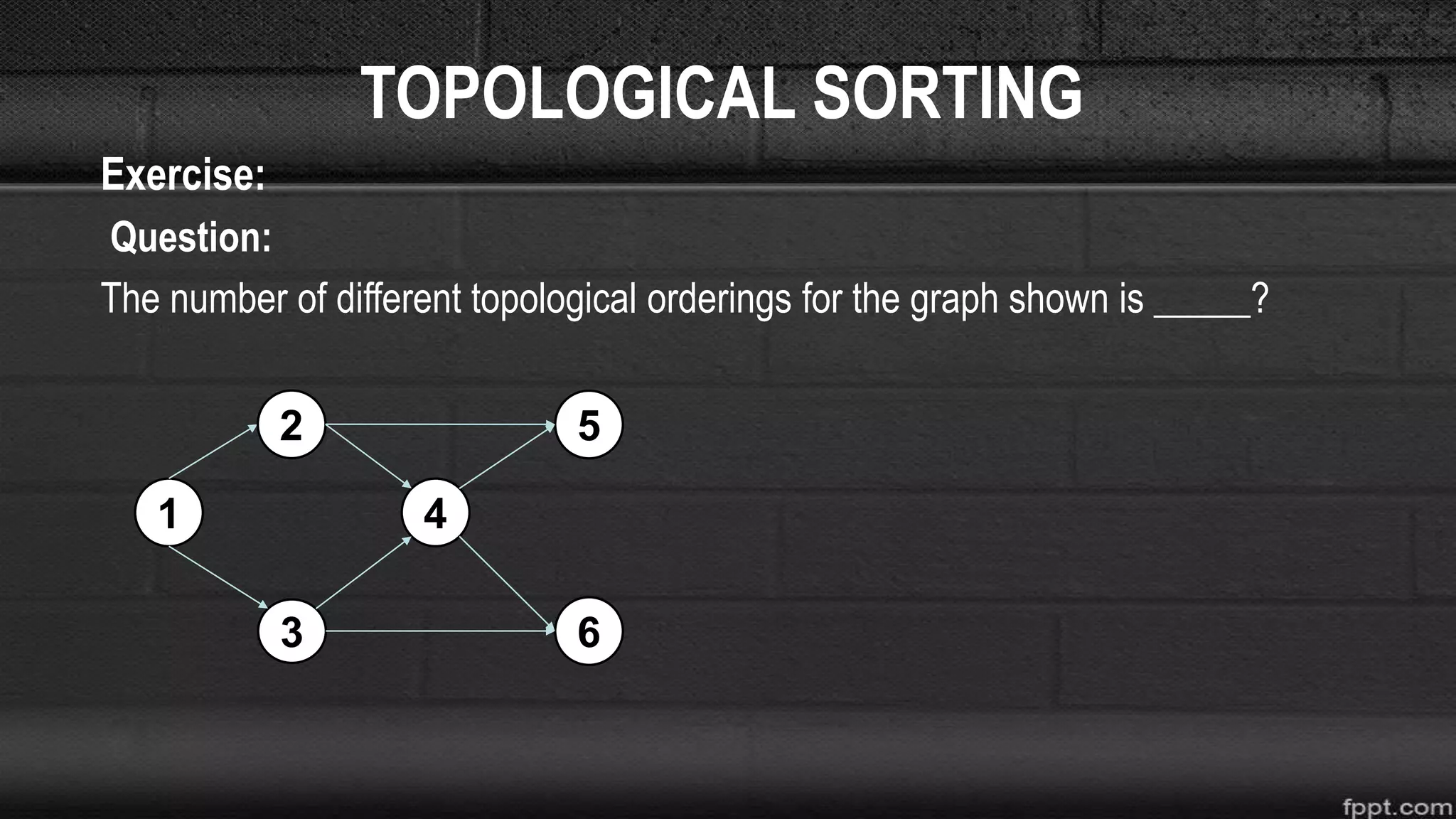
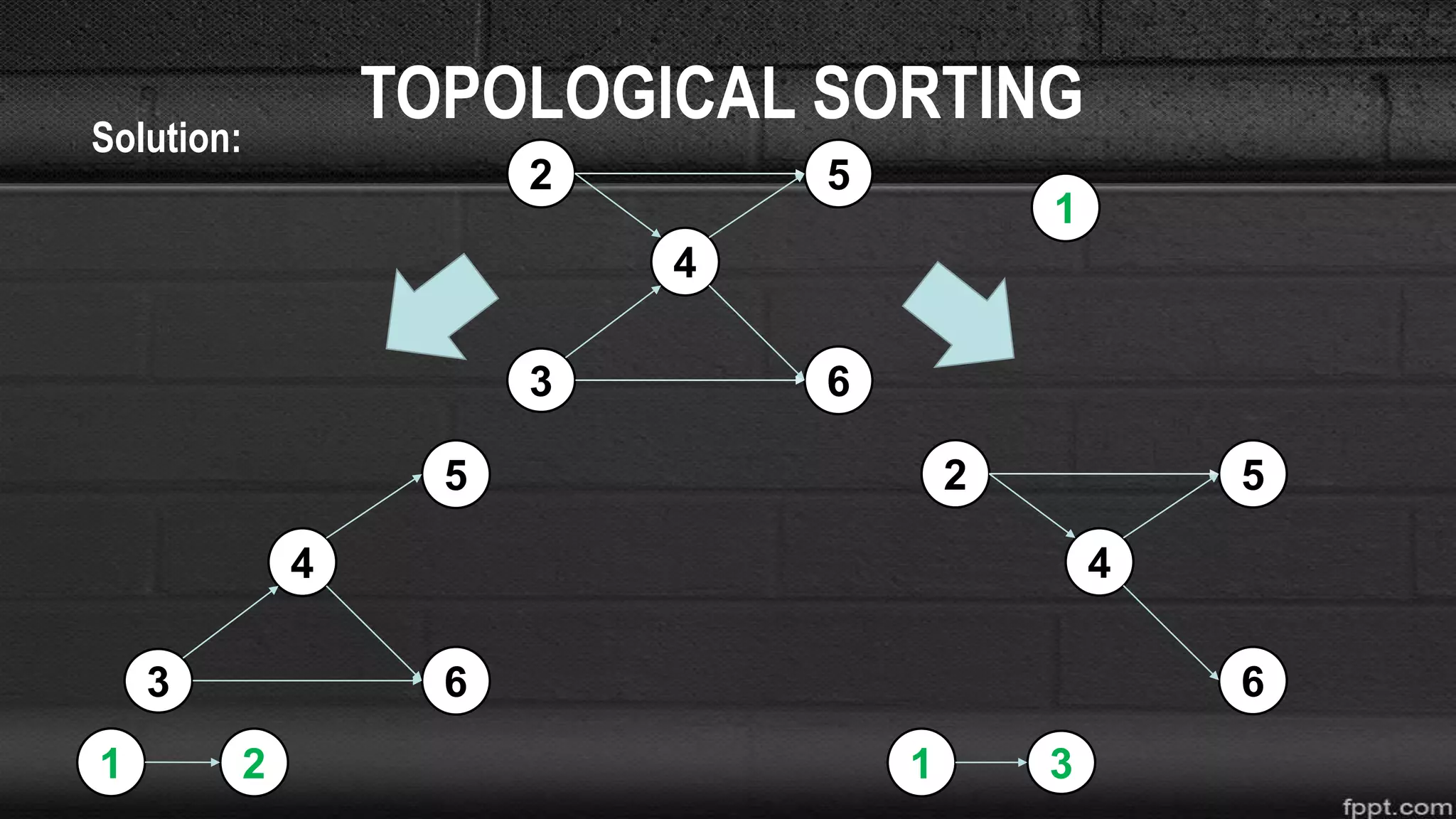
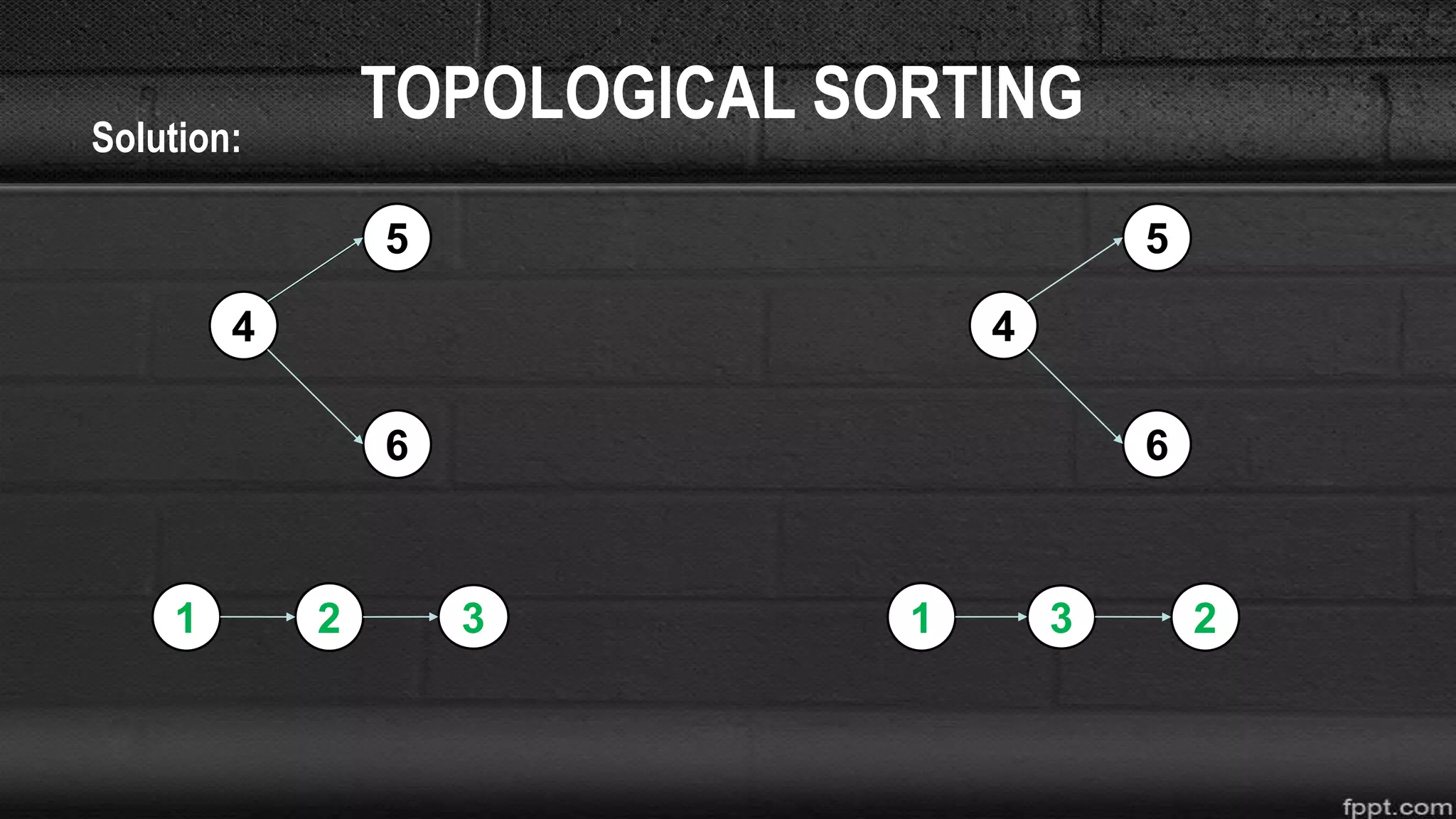
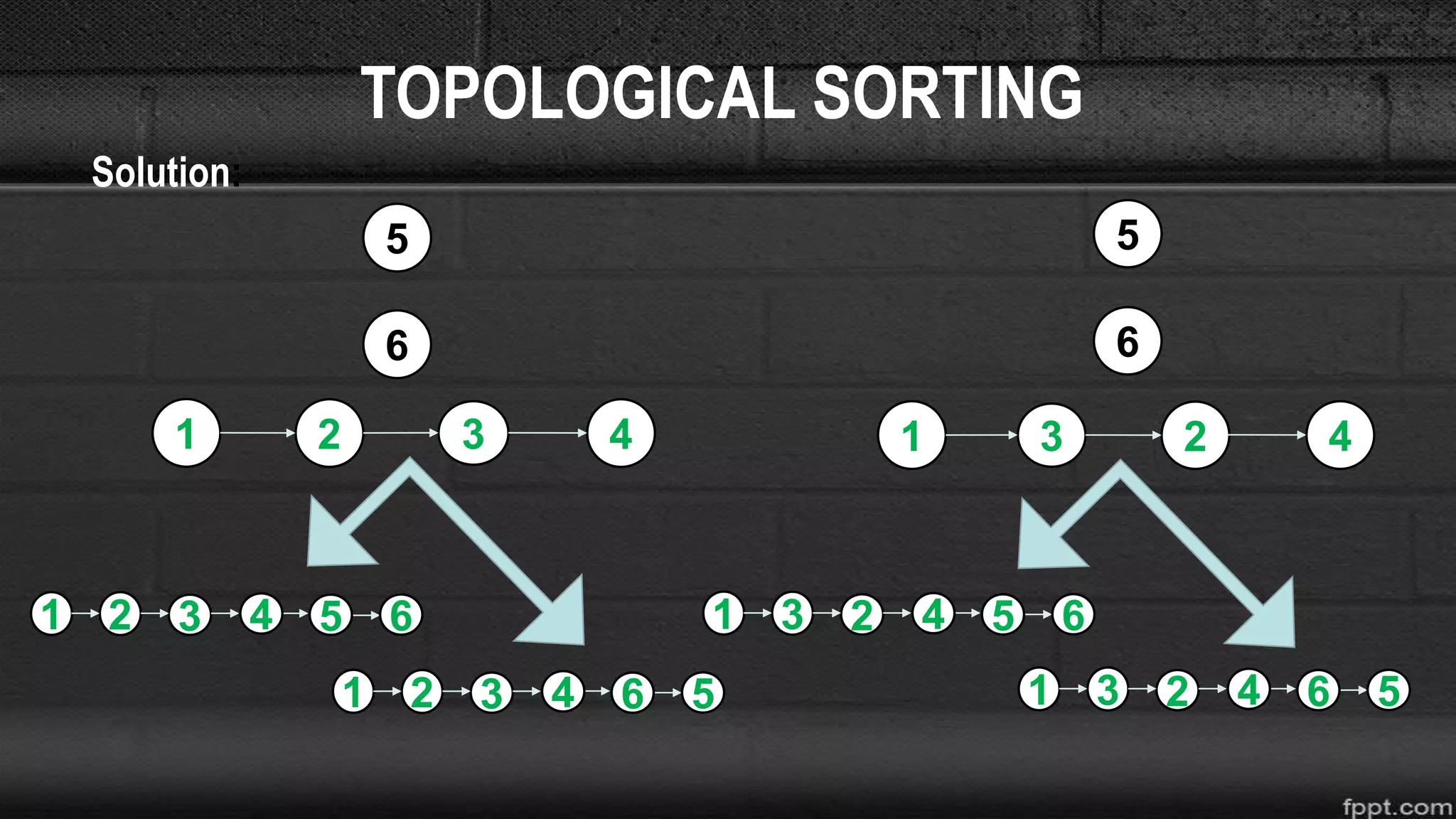
The document discusses different graph algorithms including topological sorting and Dijkstra's shortest path algorithm. It provides examples of how topological sorting works to find all possible orderings of vertices in a directed acyclic graph. It also explains the step-by-step process used in Dijkstra's algorithm to find the shortest path between a starting vertex and all other vertices in a graph.

1. CHAPTER 9
GRAPH ALGORITHMS

2. INTRODUCTION TO GRAPHS
Linear Data Structures:

3. INTRODUCTION TO GRAPHS
Non- Linear Data Structures:
Tree Graph

4. INTRODUCTION TO GRAPHS
What is a Graph?
A graph is a pictorial representation of a set of objects where some pairs of
objects are connected by links. A graph is consist of interconnected objects that
are represented by points termed as vertices.
Formally, a graph is a pair of
sets G= (V, E),
where V is the set of vertices and
E is the set of edges
*V = {a, b, c, d, e}
*E = {ab, bc, bd, cd, ce, de}

5. INTRODUCTION TO GRAPHS
Types of Graphs
• Directed Graph or digraph
 where pairs are ordered pairs
• Undirected Graph
 where pairs are unordered pairs

6. INTRODUCTION TO GRAPHS
World Systems Modeled using the Graph
Directed Graph

7. INTRODUCTION TO GRAPHS
World Systems Modeled using the Graph (cont.)

8. TOPOLOGICAL SORTING
Topological Sorting of vertices of a Directed Acyclic Graph (DAG)
is a linear ordering of the vertices in such a way that if there is an edge in
the DAG going from vertex u to vertex v then u comes before v in the ordering.
What is DAG?
• Directed - edges on the graph has directions
• Acyclic- does not contain any cycle
• Graph- has vertices & edges

9. TOPOLOGICAL SORTING
Example:
Notes:
1. Topological sorting is not possible if the
graph is not DAG.
2. There may exist multiple topological
orderings for the given DAG.

10. TOPOLOGICAL SORTING
Applications:
• Scheduling jobs from the given dependencies among jobs.
• Instruction scheduling
• Determining the order of compilation tasks to perform in making files
• Data serialization

11. TOPOLOGICAL SORTING
Question:
The number of different topological orderings for the graph is shown is _____?
0 1 Step 1: Write indegree of each vertex.
2 2
2
E
C D
BA

12. TOPOLOGICAL SORTING
0 Step 2: Since vertex-A has the least indegree, so
remove vertex A and its associated edges
and update indegrees of other vertices.
1 1
2
E
C D
B
A

13. TOPOLOGICAL SORTING
Step 3: Since vertex-B has the least indegree, so
remove vertex B and its associated edges
and update indegrees of other vertices.
0 0
1
E
C D
A B

14. TOPOLOGICAL SORTING
Step 4: Now, we have 2 vertices with least indegrees. So, we will have 2 cases.
CASE 1 CASE 2
Removing C, we have Removing D, we have
0 0
1 1E
D
E
C
A B A BC D

15. TOPOLOGICAL SORTING
Step 5:
CASE 1
*Thus, for the given graph, 2 different
topological orderings are possible.
i. ABCDE
ii. ABDCE
CASE 2
A B
A B
C
D
D E
C E

16. TOPOLOGICAL SORTING
Exercise:
Question:
The number of different topological orderings for the graph shown is _____?
3
1 4
6
52

17. TOPOLOGICAL SORTINGSolution:
3
4
6
52
3
4
6
5
2 3
4
6
52
1
1 1

18. TOPOLOGICAL SORTINGSolution:
3
4
6
5
2 3
4
6
5
21 1
5

19. TOPOLOGICAL SORTING
Solution:
3 4
6
5
2 3
6
5
21 1 4
321 4 5 6
321 4 6 5 231 4 6 5
231 4 5 6

20. TOPOLOGICAL SORTING
Thus, for the given graph, total 4 topological orderings are possible.
i. 123456
ii. 123465
iii. 132456
iv. 132465

21. SHORTEST-PATH ALGORITHM
Dijkstra’s Shortest- path algorithm
-invented by the late Edsger Wybe Dijkstra who
was aDutchsystems scientist. The objective of the
algorithm is to find the shortest path between in
any 2 vertices in a graph.

22. SHORTEST-PATH ALGORITHM
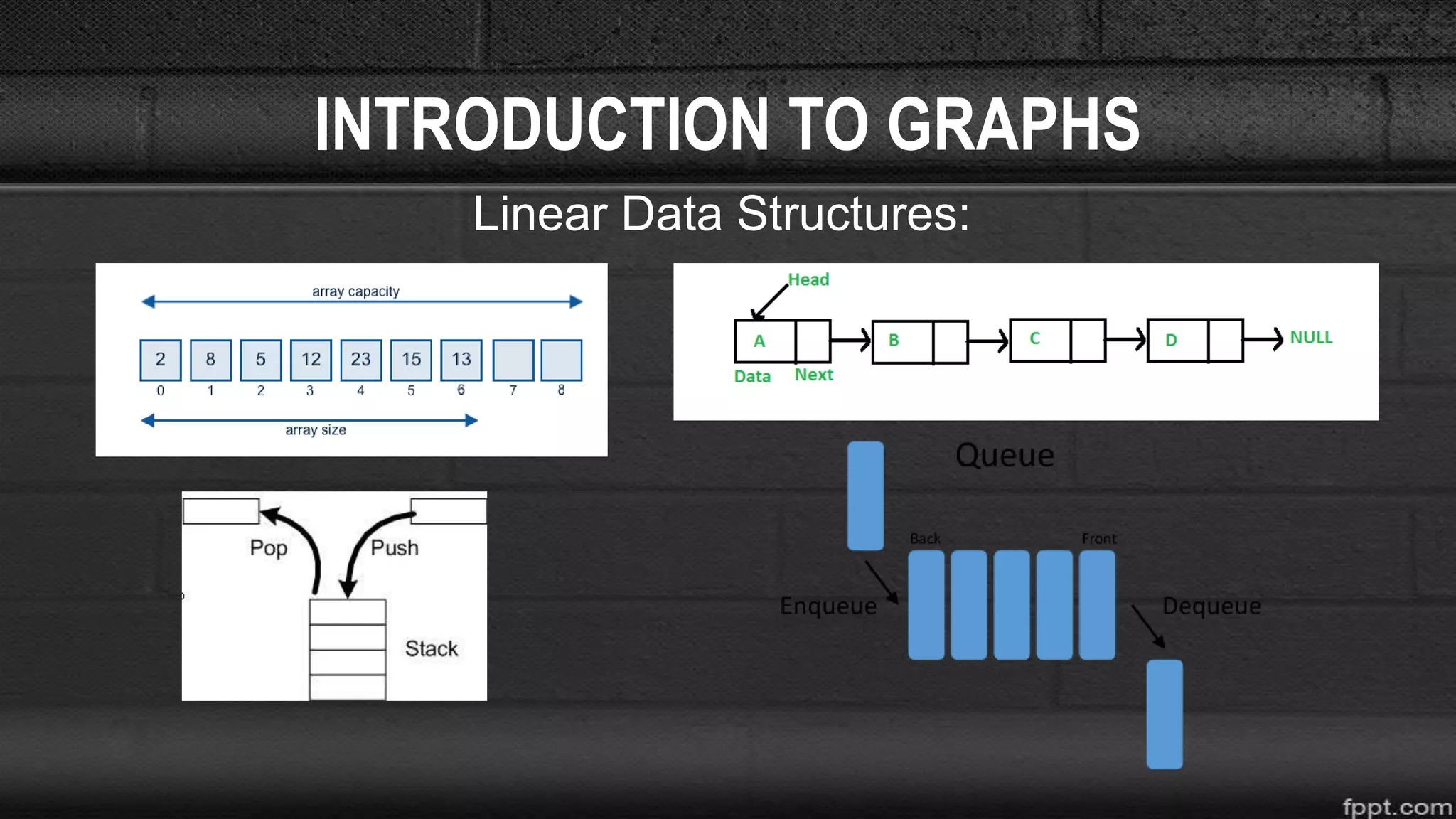
Dijkstra’s Shortest- path algorithm
• Find the shortest path from vertex A to every other vertex.
Visited = [ ] Unvisited = [ A,B,C,D,E ]

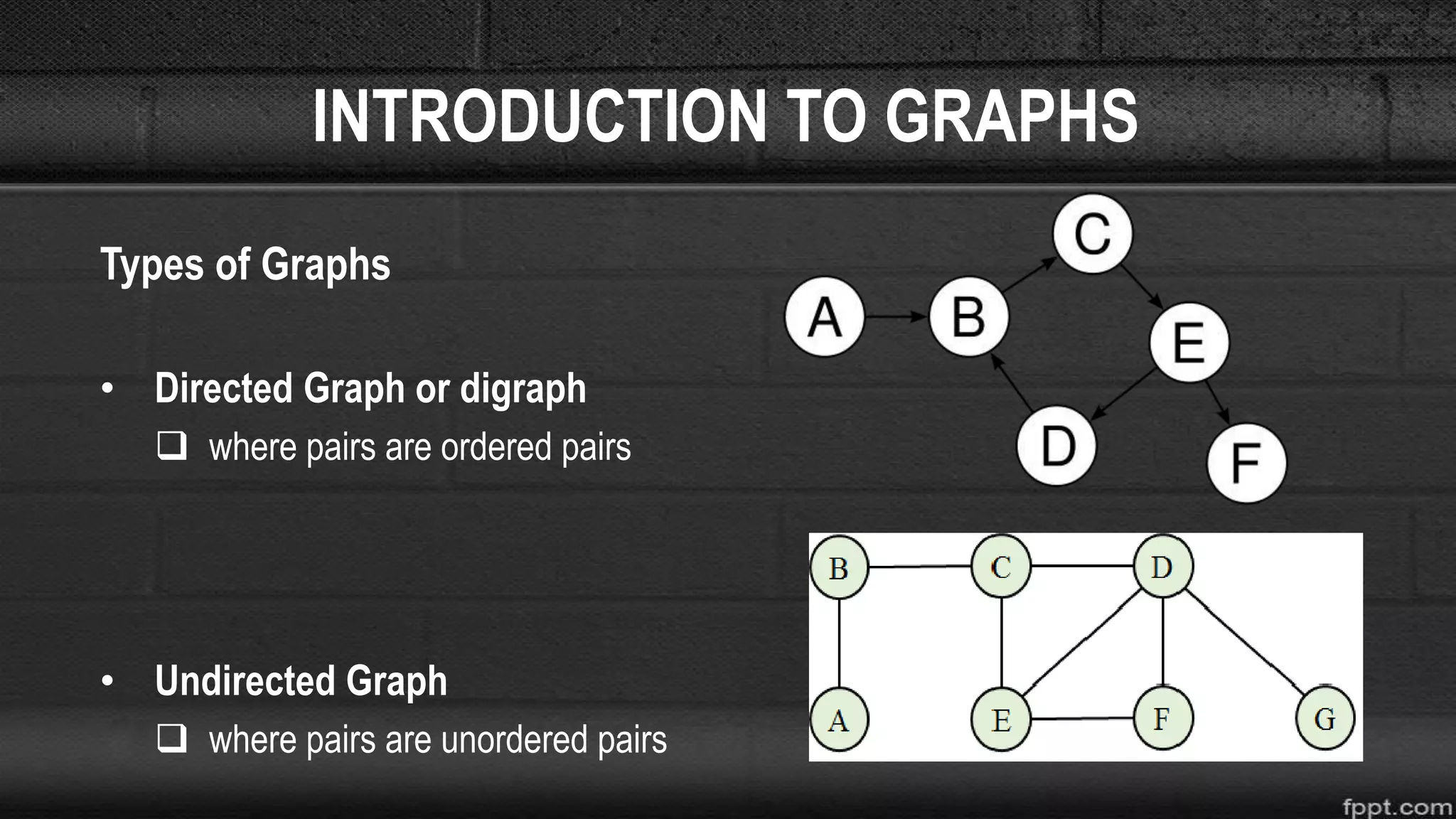
23. SHORTEST-PATH ALGORITHM
• Consider the start vertex, A
• Distance to A from a = 0
• Distance to all vertices from A are unknown, therefore ∞ (infinity)
• Visit the unvisited vertex with the smallest known distance from the start vertex.
• First time around, this is the start vertex itself, A
Visited = [ ] Unvisited = [ A,B,C,D,E ]

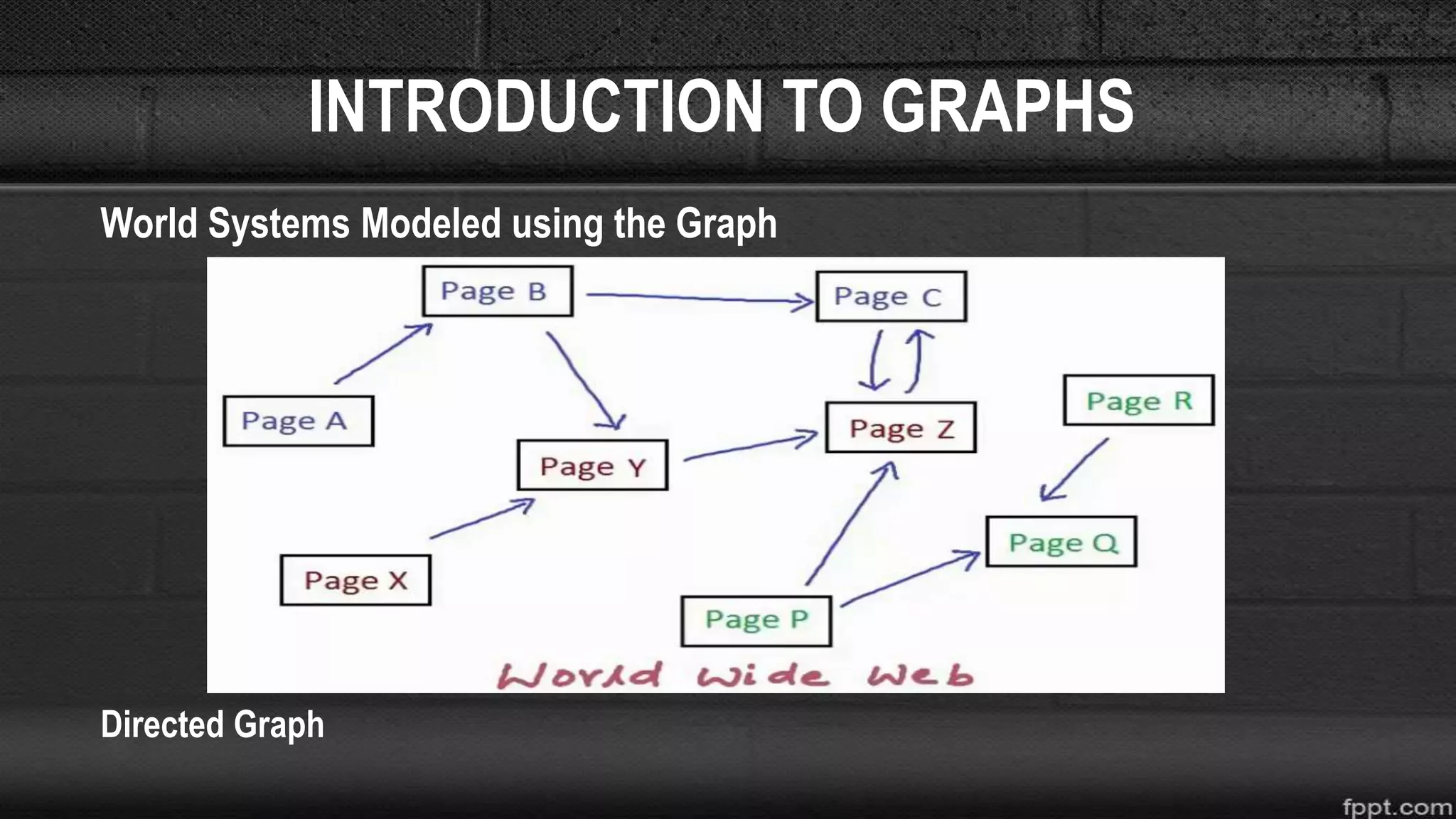
24. SHORTEST-PATH ALGORITHM
• For the current vertex, examine its unvisited neighbors
• We are currently visiting A and its unvisited neighbors are B and D
• For the current vertex, calculate the distance of each neighbor from the start vertex
• If the calculated distance of a vertex is less than the known distance, update the shortest
distance
Visited = [ ] Unvisited = [ B,C,D,E ]

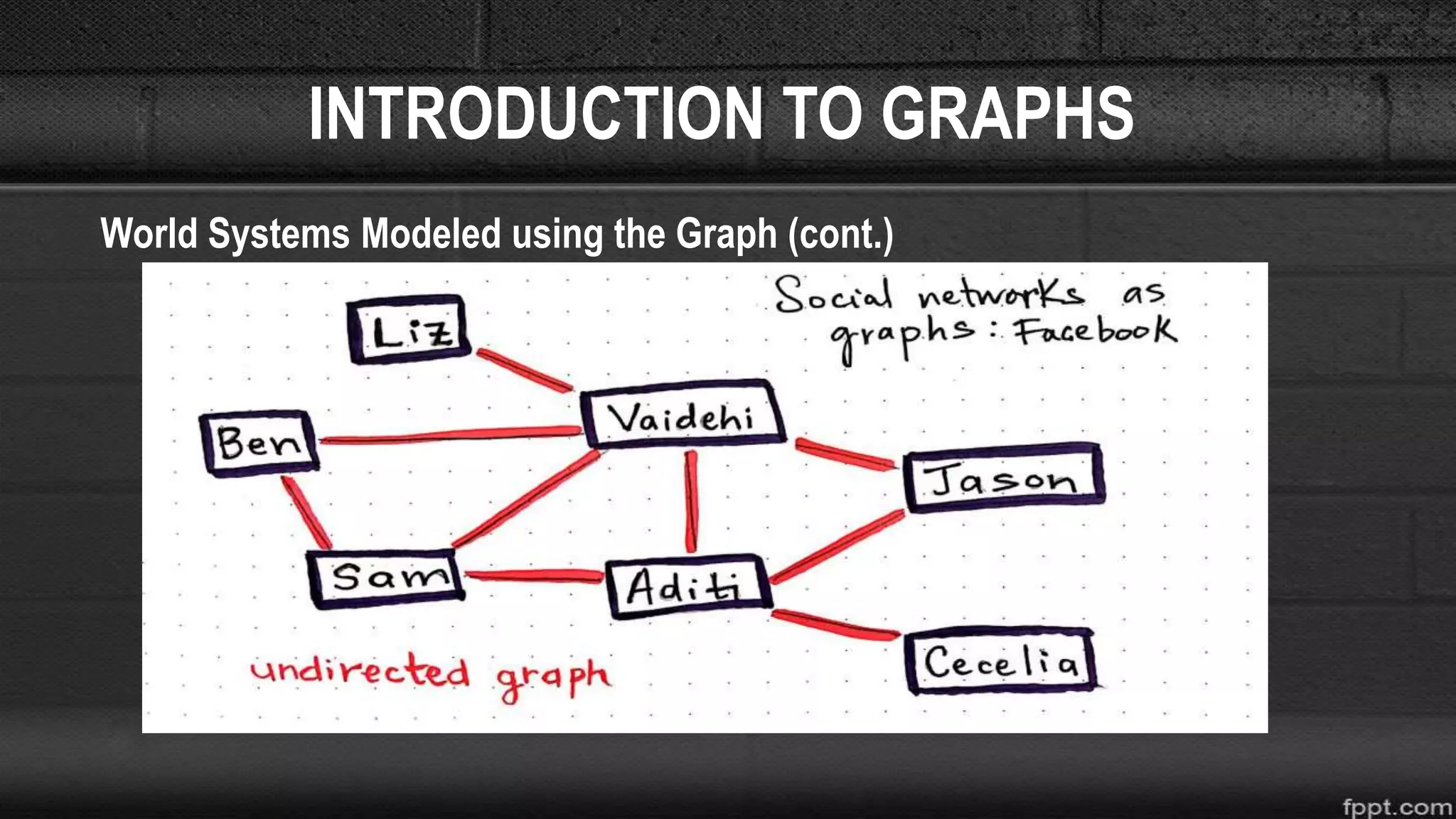
25. SHORTEST-PATH ALGORITHM
• Visit the unvisited vertex with the smallest known distance from the start vertex.
•This time around, it is vertex D
• For the current vertex, calculate the distance of each neighbor from the start vertex
• If the calculated distance of a vertex is less than the known distance, update the
shortest distance
Visited = [ A ] Unvisited = [ B,C,D,E ]

26. SHORTEST-PATH ALGORITHM
• For the current vertex, examine its unvisited neighbors
• We are currently visiting D and its unvisited neighbors are B and E
• For the current vertex, calculate the distance of each neighbor from the start vertex
• If the calculated distance of a vertex is less than the known distance, update the
shortest distance
• For the current vertex, calculate the distance of each neighbor from the start
vertex
• If the calculated distance of a vertex is less than the known distance, update
the shortest distance
• Update the previous vertex for each of the updated distances
• In this case, we visited B and E via D

27. SHORTEST-PATH ALGORITHM
• Same format
Visited = [A,D ] Unvisited = [ B,C,E ]

28. SHORTEST-PATH ALGORITHM
• Visit the unvisited vertex with the smallest known distance from the
start vertex.
•This time around, it is vertex B
Visited = [A,D,E ] Unvisited = [ B,C ]

29. SHORTEST-PATH ALGORITHM
• For the current vertex, examine its unvisited neighbors
• We are currently visiting B and its unvisited neighbors is C
• For the current vertex, calculate the distance of each neighbor from
the start vertex
• If the calculated distance of a vertex is less than the known
distance, update the shortest distance
• We do not need to update the distance to C
• No distances were updated, so we don’t need to do either
• Add the current vertex to the list of visited vertices

30. SHORTEST-PATH ALGORITHM
• Visit the unvisited vertex with the smallest known distance from the
start vertex.
•This time around, it is vertex C
• For the current vertex, examine its unvisited neighbors
• We are currently visiting C and it has no unvisited neighbors

31. SHORTEST-PATH ALGORITHM
• Add the current vertex to the list of visited vertices
Visited = [A,D,E,B,C ] Unvisited = [ ]

32. THE END