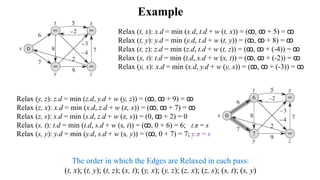
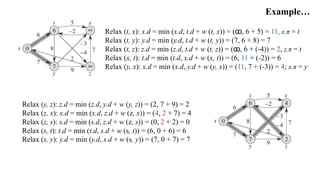
The Bellman-Ford algorithm addresses the single-source shortest-paths problem for directed graphs with potentially negative edge weights, returning whether a negative-weight cycle exists and producing shortest path estimates if not. It works by repeatedly relaxing edges up to |V| - 1 times, where V is the set of vertices, and operates in O(VE) time. The algorithm guarantees correct shortest path calculations if no negative cycles are reachable from the source and provides a framework for vertex predecessors to construct these paths.