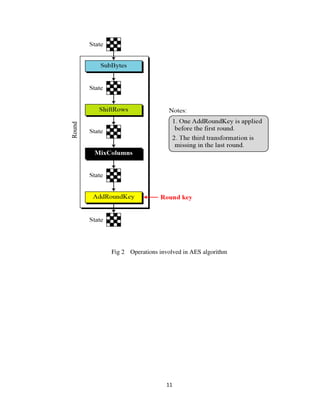
This document describes a student project to implement the Advanced Encryption Standard (AES) in Verilog. AES is a symmetric block cipher that uses 128-bit blocks and 128/192/256-bit keys. The project aims to develop optimized and synthesizable Verilog code to encrypt and decrypt 128-bit data using AES. The document provides background on cryptography, AES, and its algorithm which includes key expansion, substitution, transposition, and mixing operations. It also outlines the implementation, encryption, decryption, and performance estimation aspects of the project.

1. 1
Verilog Design and Implementation
of
ADVANCED ENCRYPTION STANDARD (AES)
Hardik Manocha Samnit Dua
Student Student
Electronics & Communication Engineering Electronics & Communication Engineering
G B Pant Government Engineering College G B Pant Government Engineering College
Delhi, India Delhi, India
manochahardik94@gmail.com samnitdua@gmail.com
9811939537 9013290517
Nivedita Wasson
Student
Electronics & Communication Engineering
G B Pant Government Engineering College
Delhi, India

2. 2
CONTENTS
Page Nos.
List of figures 4
Abstract 5
1. Project Overview 5-6
1.1. Introduction 5
1.2. Objective 6
2. The Advanced Encryption Standard (AES) 6-8
2.1. Introduction to Cryptography 6
2.2. Introduction to the Advanced Encryption Standard 7
2.3. Description of the cipher 8
3. AES Algorithm description 10-12
3.1. Description of the algorithm 10
3.2. The Rijndael Key Schedule 12
4. AES operations 13-20
4.1. The SubBytes operation 13
4.2. The ShiftRow operation 16
4.3. The MixColumn operation 18
4.4. The AddRoundKey operation 20
5. Implementation of the Algorithm 21-23
5.1. Implementation 21
5.2. Encryption 22
5.3. Decryption 22
5.4. Performance Estimation 23

3. 3
6. Conclusion, future scope and applications 23-25
6.1. Conclusion 23
6.2. Future scope 24
6.3. Applications 24
References 26

4. 4
List of figures Page No.
Fig 1 Cipher description 13
Fig 2 Operations involved in AES algorithm 15
Fig 3 AES Key Scheduling 16
Fig 4 SubBytes step 18
Fig 5 S-box implementation on the state matrix 19
Fig 6 SubBytes Table 19
Fig 7 InvSubBytes Table 20
Fig 8 An example of SubBytes and 20
InvSubBytes transformations
Fig 9 Shift Rows Scheme 21
Fig 10 An example of ShiftRows and InvShiftRows 22
Fig 11 MixColumns Scheme 23
Fig 12 Mix Column and Inv Mix Column 24
Fig 13 An example of AES mix columns operation 25
Fig 14 AddRoundKey Scheme 27
Fig 15 Encryption 29
Fig 16 Decryption 30
Fig 17 Performance Estimation Table 31

5. 5
ABSTRACT
On October, 2, 2000, The National Institute of Standards and Technology (NIST)
announced Rijndael as the new Advanced Encryption Standard (AES).The predecessor to
the AES was Data Encryption Standard (DES) which was considered to be insecure
because of its vulnerability to brute force attacks. DES was a standard from 1977 and
stayed until the mid 1990’s. However, by the mid 1990s, it was clear that the DES’s 56-
bit key was no longer big enough to prevent attacks mounted on contemporary
computers, which were thousands of times more powerful than those available when the
DES was standardized. The AES is a 128 bit Symmetric block Cipher.
This project includes the complete step by step implementation of Advanced Encryption
Technique, i.e. encrypting and decrypting 128 bit data using the AES and it’s
modification for enhanced reliability and security. The encryption process consists of the
combination of various classical techniques such as substitution, rearrangement and
transformation encoding techniques. The encryption and decryption modules include the
Key Expansion module which generates Key for all iterations. The modifications include
the addition of an arithmetic operation and a route transposition cipher in the attacks
iterative rounds. The key expansion module is extended to double the number of iterative
processing rounds in order to increase its immunity against unauthorized attacks.
1 Project Overview
1.1 Introduction
Encryption is the most effective way to achieve data security. The Advanced Encryption
Standard (AES), also known as Rijndael (its original name), is a specification for the
encryption of electronic data established by the U.S. National Institute of Standards and
Technology (NIST) in 2001.

6. 6
The aim of the project is to achieve an efficient Verilog implementation of 128bit block
and 128 bit key AES cryptosystem. An Optimized and Synthesizable Verilog code is
developed for the implementation of both 128 bit data encryption and decryption process
& description is verified using Xilinx.
1.2 Objective
In today's electronic age, the importance of digital cryptography in securing electronic
data transactions is unquestionable. Every day, users electronically generate and
communicate a large volume of information with others. This information includes
medical, financial and legal files; automatic and Internet banking; phone conversations;
pay-per-view television; and other e-commerce transactions. To meet these requirements,
Advanced Encryption Standard (AES) for the encryption of electronic data can be used.
Here we are going to achieve an efficient Verilog implementation of 128bit block and
128 bit key AES cryptosystem.
2 The Advanced Encryption Standard (AES)
2.1 Introduction to Cryptography
Cryptography or cryptology is the practice and study of techniques for secure
communication in the presence of third parties (called adversaries).Cryptography prior to
the modern age was effectively synonymous with encryption, the conversion of
information from a readable state to apparent nonsense. Modern cryptography is heavily
based on mathematical theory and computer science practice; cryptographic algorithms
are designed around computational hardness assumptions, making such algorithms hard
to break in practice by any adversary. It is theoretically possible to break such a system,
but it is infeasible to do so by any known practical means. These schemes are therefore

7. 7
termed computationally secure; theoretical advances, e.g., improvements in integer
factorization algorithms, and faster computing technology require these solutions to be
continually adapted. There exist information-theoretically secure schemes that provably
cannot be broken even with unlimited computing power but these schemes are more
difficult to implement than the best theoretically breakable but computationally secure
mechanisms.
Until modern times, cryptography referred almost exclusively to encryption, which is the
process of converting ordinary information (called plaintext) into unintelligible text
(called cipher text). Decryption is the reverse, in other words, moving from the
unintelligible cipher text back to plaintext. In cryptography, a cipher (or cipher) is
an algorithm for performing encryption or decryption—a series of well-defined steps that
can be followed as a procedure. The detailed operation of a cipher is controlled both by
the algorithm and in each instance by a "key".
2.2 Introduction to the Advanced Encryption Standard
The Advanced Encryption Standard (AES), also known as Rijndael (its original name), is
a specification for the encryption of electronic data established by the U.S. National
Institute of Standards and Technology (NIST) in 2001.AES is based on the Rijndael
cipher developed by two Belgian cryptographers, Joan Daemen and Vincent Rijmen, who
submitted a proposal to NIST during the AES selection process. Rijndael is a family of
ciphers with different key and block sizes. For AES, NIST selected three members of the
Rijndael family, each with a block size of 128 bits, but three different key lengths: 128,
192 and 256 bits. AES has been adopted by the U.S. government and is now used
worldwide. It supersedes the Data Encryption Standard (DES), which was published in
1977. The algorithm described by AES is a symmetric-key algorithm, meaning the same
key is used for both encrypting and decrypting the data. In the United States, AES was
announced by the NIST as U.S. FIPS PUB 197 (FIPS 197) on November 26, 2001.This
announcement followed a five-year standardization process in which fifteen competing

8. 8
designs were presented and evaluated, before the Rijndael cipher was selected as the most
suitable.AES became effective as a federal government standard on May 26, 2002 after
approval by the Secretary of Commerce.AES is included in the ISO/IEC 18033-3
standard.
AES is available in many different encryption packages, and is the first publicly
accessible and open cipher approved by the National Security Agency (NSA) for top
secret information when used in an NSA approved cryptographic module. The name
Rijndael is a play on the names of the two inventors (Joan Daemen and Vincent Rijmen).
It is also a combination of the Dutch name for the Rhine River and a dale.
2.3 Description of the cipher
AES is based on a design principle known as a substitution-permutation network,
combination of both substitution and permutation, and is fast in both software and
hardware. AES is a variant of Rijndael which has a fixed block size of 128 bits, and a key
size of 128, 192, or 256 bits. By contrast, the Rijndael specification per se is specified
with block and key sizes that may be any multiple of 32 bits, both with a minimum of
128 and a maximum of 256 bits.AES operates on a 4×4 column-major order matrix of
bytes, termed the state, although some versions of Rijndael have a larger block size and
have additional columns in the state. Most AES calculations are done in a special finite
field. For instance, if you have 16 bytes, b0, b1... b15, these bytes are represented as this
matrix:

9. 9
The key size used for an AES cipher specifies the number of repetitions of transformation
rounds that convert the input, called the plaintext, into the final output, called the cipher
text. The number of cycles of repetition is as follows:
10 cycles of repetition for 128-bit keys.
12 cycles of repetition for 192-bit keys.
14 cycles of repetition for 256-bit keys.
Each round consists of several processing steps, each containing four similar but different
stages, including one that depends on the encryption key itself. A set of reverse rounds
are applied to transform cipher text back into the original plaintext using the same
encryption key.
Fig 1 Cipher description

10. 10
3 AES Algorithm description
3.1 Description of the algorithm
1. KeyExpansions—round keys are derived from the cipher key using Rijndael’s key
schedule. AES requires a separate 128-bit round key block for each round plus one more.
2. InitialRound
(a) AddRoundKey—each byte of the state is combined with a block of the round key
using bitwise xor.
3. Rounds
(a) SubBytes—a non-linear substitution step where each byte is replaced with another
according to a lookup table.
(b) ShiftRows—a transposition step where the last three rows of the state are shifted
cyclically a certain number of steps.
(c) MixColumns—a mixing operation which operates on the columns of the state,
combining the four bytes in each column.
(d) AddRoundKey
4. Final Round (no MixColumns)
(a) SubBytes
(b) ShiftRows
(c) AddRoundKey

11. 11
Fig 2 Operations involved in AES algorithm

12. 3.2 The Rijndael Key Schedule
The Key Schedule is responsible for expanding a short key into a larger key,
are used during the different iterations. Each key size is expanded
An 128 bit key is expanded to an 176 byte key.
An 192 bit key is expanded to an 208 byte key.
An 256 bit key is expanded to an 240 byte key.
There is a relation between
Key size. For an 128-bit key, there is one initial AddRoundKey
10 rounds and each round needs a new 16 byte key, therefore we requ
Keys of 16 byte, which equa
cipher key sizes. The general formula is
ExpandedKeySize = (nbrRounds+1) * BlockSize
This step takes 128-bits (16
12
The Rijndael Key Schedule
The Key Schedule is responsible for expanding a short key into a larger key,
used during the different iterations. Each key size is expanded to a different size:
An 128 bit key is expanded to an 176 byte key.
An 192 bit key is expanded to an 208 byte key.
An 256 bit key is expanded to an 240 byte key.
There is a relation between the cipher key size, the number of rounds and the
bit key, there is one initial AddRoundKey operation plus there are
and each round needs a new 16 byte key, therefore we require 10+1 Round
which equals 176 byte. The same logic can be applied to the two other
cipher key sizes. The general formula is that:
ExpandedKeySize = (nbrRounds+1) * BlockSize
Fig 3 AES Key Scheduling
bits (16-bytes) key and expands into array of 44 32-bit
The Key Schedule is responsible for expanding a short key into a larger key, whose parts
to a different size:
the cipher key size, the number of rounds and the Expanded
ration plus there are
ire 10+1 Round
same logic can be applied to the two other
bit words.

13. 13
4 AES operations:
4.1 The SubBytes operation
The SubBytes operation is a non-linear byte substitution, operating on each byte of the
state independently. The substitution table (S-Box) is invertible and is constructed by
the composition of two transformations:
1. Take the multiplicative inverse in Rijndael's finite field
2. Apply an affine transformation which is documented in the Rijndael documentation.
Since the S-Box is independent of any input, pre-calculated forms are used. Each byte of
the state is then substituted by the value in the S-Box whose index corresponds to the
value in the state:

14. 14
b (i,j) = SBox[a(i,j)]
The inverse of SubBytes is the same operation, using the inversed S-Box, which is also
precalculated.
Fig 4 SubBytes step
In the SubBytes step, each byte in the state is replaced with
its entry in a fixed 8-bit lookup table, S; b(i,j) = S(i,j)
Fig 5 S-box implementation on the state matrix

15. 15
SubBytes Table
Fig 6 SubBytes Table
InvSubBytes Table
Fig 7 InvSubBytes Table

16. 16
Sample SubByte Transformation
The SubBytes and InvSubBytes transformations are inverses of each other.
Fig 8 An example of SubBytes and InvSubBytes transformations
4.2 The ShiftRow operation
In this operation, each row of the state is cyclically shifted to the left, depending on the
row index.
The 1st row is shifted 0 positions to the left.
The 2nd row is shifted 1 position to the left.
The 3rd row is shifted 2 positions to the left.
The 4th row is shifted 3 positions to the left.
The inverse of Shift Row is the same cyclically shift but to the right. It is needed later for
decoding.

17. 17
Fig 9 Shift Rows Scheme
In the ShiftRows step, bytes in each row of the state are shifted cyclically to the left. The number
of places each byte is shifted differs for each row.
ShiftRows and InvShiftRows
Fig 10 An example of ShiftRows and InvShiftRows

18. 4.3 The MixColumn operation
In the MixColumns step, the four bytes of each column
an invertible linear transformation
and outputs four bytes, where each input byte
ShiftRows, MixColumns provides
During this operation, each column is tran
multiplied by column gives new
This can also be seen as the following:
18
The MixColumn operation
In the MixColumns step, the four bytes of each column of the state are combined using
transformation. The MixColumns function takes four bytes
and outputs four bytes, where each input byte affects all four output bytes. Together with
MixColumns provides diffusion in the cipher.
ion, each column is transformed using a fixed matrix (matrix
multiplied by column gives new value of column in the state):
This can also be seen as the following:
Fig 11 MixColumns Scheme
the state are combined using
. The MixColumns function takes four bytes as input
affects all four output bytes. Together with
a fixed matrix (matrix

19. The MixColumns operation has the followi
19
The MixColumns operation has the following inverse (numbers are decimal)
Or:
Fig 12 Mix Column and Inv Mix Column
(numbers are decimal):
Mix Column and Inv Mix Column

20. Fig 13
4.4 The AddRoundKey operation
In this operation, a Round Key is applied to the state by a simple bitwise XOR.
The Round Key is derived from the Cipher Key by the means of the key schedule.
The Round Key length is equal to the block key length (=16 bytes).
In the AddRoundKey step, the subkey is combined with
subkey is derived from the
same size as the state. The subkey is added by combining
corresponding byte of the
In the AddRoundKey step, each byte of the state is combined with a byte of the round
subkey using the XOR operation.
20
13 An example of AES mix columns operation
The AddRoundKey operation
In this operation, a Round Key is applied to the state by a simple bitwise XOR.
The Round Key is derived from the Cipher Key by the means of the key schedule.
The Round Key length is equal to the block key length (=16 bytes).
the AddRoundKey step, the subkey is combined with the state. For each round, a
subkey is derived from the main key using Rijndael’s key schedule; each subkey is the
same size as the state. The subkey is added by combining each byte of the state with the
rresponding byte of the subkey using bitwise XOR.
In the AddRoundKey step, each byte of the state is combined with a byte of the round
operation.
In this operation, a Round Key is applied to the state by a simple bitwise XOR.
The Round Key is derived from the Cipher Key by the means of the key schedule.
the state. For each round, a
; each subkey is the
each byte of the state with the
In the AddRoundKey step, each byte of the state is combined with a byte of the round

21. 21
Fig 14 AddRoundKey Scheme
5 Implementation of the Algorithm
5.1 Implementation
The AES 128 algorithm is implemented using Verilog coding in Xilinx ISE 13.2. First,
the Algorithm’s Encryption module is designed with the Key Expansion unit. After
designing this encryption module, the next step is to design Decryption module
separately. After this, a Top module is designed where Encryption and Decryption
modules are instantiated. Also Top module is designed with Memory to hold the values
of Key generated in Encryption so that Decryption Module can use those values.
aes_top
clk
rst_enc
rst_dec
Encryption
Module
Key
Expansion
Module
Key
Memory
Decryption
Module
Plain Text
Cipher Key
Data Match

22. 22
5.2 ENCRYPTION
data_in= 128’h343aaf5503e7d407ea507d41f4eeda64
key_in= 128’h155e57340f09e90d2e500c78735555e8
cipher_data= 128’h575cb0c3b04b719f0ec0e59131db183b
Fig 15 Encryption
5.3 DECRYPTION
data_match=1’b1
Fig 16 Decryption

23. 23
5.4 PERFORMANCE ESTIMATION
for aes_top.v module on Virtex 4 (Device= XC4VLX60 & Package= FF1148)
Parameter Haswell Architecture Enhanced Pentium
Architecture
Time (ns) 4.258 4.296
Frequency (MHz) 234.864 232.793
Throughput (Gbps) 3.006 2.979
Throughput/slice
(Mbps/slice) 399.15 183.952
Fig 17 Performance Summary
6 Conclusion, future scope and applications
6.1 Conclusion
The Advanced Encryption Standard algorithm is an iterative private key symmetric block
cipher that can process data blocks of 128 bits through the use of cipher keys with lengths
of 128, 192, and 256 bits. An efficient Verilog implementation of 128bit block and 128

24. 24
bit key AES cryptosystem has been presented in this project. An Optimized and
Synthesizable Verilog code is developed for the implementation of both 128 bit data
encryption and decryption process & description is verified using Xilinx.
6.2 Future Scope
One could work on selection of a larger key size which would make the algorithm is
more secure, and a larger input block to increase the throughput. The extra increase in
area can however be tolerated. So such an algorithm with high level of security and high
throughput can have ideal applications such as in multimedia communications.
Furthermore study of optimization approaches for the implementations supporting
multiple key lengths and modes of operation have tremendous scope for future work.
6.3 Applications
The following examples, as well as many other applications, require a great deal of
security in the storage and transportation of this information.
Voice Communications
There is a potentially significant market for high-strength encryption on VoIP, wireless
phone, and land-line phone communications. The perceived threat of eavesdropping is a
powerful market driver in the world of personal communications. Expect Nokia,
Ericsson, Samsung, Motorola, TI, Casio, and the other major phone makers to move in,
along with a cadre of startups that hope to provide the IP. Once one major vendor offers
encryption on a popular phone then, rapidly, every other vendor will be forced to follow
suit or lose business to competition. In the space of 18-24 months, encryption mode will
become the default talk mode. Expect every VoIP system and land-line phone to gain this
functionality as well.

25. 25
Network Appliances
Another potentially large market for digital encryption is network appliances—anything
electronic that is interactively hooked up to a network. As the number of non-PC and
wireless devices accessing the Internet increases, the rate of cyber attacks on network
infrastructure and service providers will increase. Critical functions such as power-grid
management and water-distribution systems are shifting to the Web and need to be
protected. Even simple appliances such as fire alarms or temperature alarms can be
vulnerable to hacker attacks. There is great value in preventing a hacker from
electronically yelling,"fire"
Secure Socket Layer (SSL)
SSLs provide security using the Secure Socket Layer protocol for Internet browser-based
transactions (in other words, SSL is Web specific). The presence of encryption on a Web
site is often the deciding factor whether to make an online transaction; no company wants
to lose business for lack of a secure connection. As bandwidth requirements go up, it is
vital to include a resident SSL hardware accelerator in the data center to encode and
decode traffic going in and out of the Web site.
Virtual Private Network (VPN)
VPNs protect direct connections between users and enterprise networks. The high cost of
dedicated telecom links compels transition from software to hardware support for these
links. Dedicated lease lines are relatively private and secure, but it's too expensive to give
everyone a private line. Putting encrypted VPN traffic on public lines is less expensive.
While few individual users require a dedicated connection at Gbit/sec speeds, the
ballooning number of VPN users means a corporate LAN will need to aggregate and
process encrypted data streams in the gigabit range now, and in the multi-gigabit range in
the near future.

26. 26
REFERENCES
[1] AES page available via http://www.nist.gov/CryptoToolkit.4
[2] Computer Security Objects Register (CSOR): http://csrc.nist.gov/csor/.
[3] J. Daemen and V. Rijmen, AES Proposal: Rijndael, AES Algorithm
Submission, September 3, 1999, available at [1].
[4] J. Daemen and V. Rijmen, The block cipher Rijndael, Smart Card research and
Applications, LNCS 1820, Springer-Verlag, pp. 288-296.
[5] B. Gladman’s AES related home page
http://fp.gladman.plus.com/cryptography_technology/.
[6] A. Lee, NIST Special Publication 800-21, Guideline for Implementing
Cryptography in the Federal Government, National Institute of Standards and
Technology, November 1999.
[7] A. Menezes, P. van Oorschot, and S. Vanstone, Handbook of Applied
Cryptography, CRC Press, New York, 1997, p. 81-83.
[8] J. Nechvatal, ET. al., Report on the Development of the Advanced Encryption
Standard (AES), National Institute of Standards and Technology, October 2, 2000,
[9] Understanding AES Inverse Mix-Columns Transformation Calculation.pdf
[10] http://www.ijsrd.com/articles/IJSRDV1I9071.pdf
[11] http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf
[12] http://www.jatit.org/volumes/Vol53No2/6Vol53No2.pdf