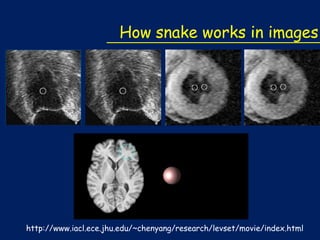
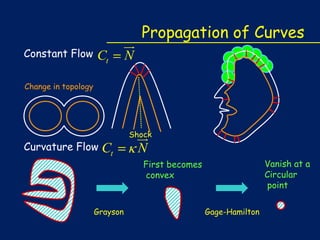
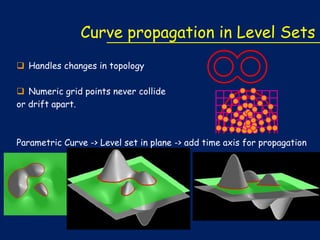
The document describes how snakes, or active contours, can be used to model shapes in images. It discusses how snakes work by defining an energy function along a curve and minimizing that energy to find the optimal curve. The energy includes an internal term based on curvature and an external term from image features. Level sets are used to propagate the curves towards the minimum energy configuration using gradient descent. Key steps include modeling the shape as a curve, defining the energy function, deriving the curve to minimize energy via calculus of variations, and propagating the curves using level sets.

1. Electrical &Computer
Engineering Department
University of Houston
Snakes in Images
Yan Xu
Bio-Image Analytics Laboratory

2. How snake works in images
http://www.iacl.ece.jhu.edu/~chenyang/research/levset/movie/index.html

3. How snake works in images
 Step 1: Model the shape by curve or surface
 Step 2: Define the energy function E along the curve
E = internal energy (curvature) + external energy (images)
 Step 3: Derive the curve to minimize the energy (calculus
of variations)
 Step 4: Propagate the curves (gradient descent) to reach
the minimum using level set (easier to implement in reality).
Keywords:
Curve
Energy
Level set

4. Snake -> Curves
Consider a closed planar curve C ( p) {x( p), y( p)}, p [0,1]
C(0.1)
S(p) is the arclength
C(0.2)
C(0.7)
C(0)
C(0.4)
C(0.95)
Cp =tangent
C(0.8)
Css
| Cp |
Css
N
N
1
C(0.9)
Cs
Cp
C
The geometric trace of the curve can be alternatively
represented implicitly as C {( x, y ) | ( x, y ) 0}
1
0
0
1

5. Properties of level sets

T
The level set normal

N
|

N
|
Proof. Along the level sets (equal 0) we have zero change,
that is s 0 , but by the chain rule
So,
s
|
( x, y )
|

,T
x
0
xs
|
y
|

,T
ys

T

N
|
|

6. Properties of Level Sets
The level set curvature
Css =div
|
|
Proof. zero change along the level sets,
ss
So,
( x, y )
d
( x xs
ds
,
|
|
y
|
ys )
|
[

,T
d
ds
x
xx s
xy
ys ,
ss

,T
d
ds
x
xy s
yy
ys ],
|
0 , also

, N
|
Numerical Geometry of Images:
http://webcourse.cs.technion.ac.il/236861/Winter2012-2013/en/ho_Tutorials.html

7. Constant Flow
Ct


N
Propagation of Curves
Change in topology
Curvature Flow
Ct
Grayson


N
Vanish at a
Circular
point
First becomes
convex
Gage-Hamilton

8. Curve propagation in Level Sets
dC
dt


VN
C(t)
d
dt
y
V
x
x, y, t
( x, y; t )
t
0
t

N
x
xt
y
yt
x xt
|
t
C(t) level set

, VN
, Ct
V
|
y
y yt

,N

,N
V
V
0
,
|
x
|
V|
|

9. Curve propagation in Level Sets
 Handles changes in topology
 Numeric grid points never collide
or drift apart.
Parametric Curve -> Level set in plane -> add time axis for propagation

10. Curve propagation in Level Sets
Some flows
Ct

VN
Ct

N
Ct
g
t
t
 
g, N N
V
2
xx y
div
t
2
xy x y
2
2
x
y
2
yy x
div g
g
2
xx y
2
xy x y
2
2
x
y
2
yy x
g,

11. Snake Model
1
arg min
C
Cp
0
2
C pp
tension
2
rigidity
2 g (C ) dp
external energy from the image
Energy
g (C )
|
[G (C ) * I (C )] |2
A snake that minimize E must satisfy the Euler equation
Cpp
Cpppp
g C
0
To find a solution
dC
dt
C pp
C pppp
g C
When C stabilizes and the term Ct vanishes, a solution is achieved.
Snakes: Active Contour Models, 1988

12. Geodesic Active Contour
arg min
C
L C
0
g C ds
ds is the Euclidean arc-length.
Trying to find minimum weighted distance
I(x)
Euler Lagrange gradient descent
Ct

g (C) n
 
g (C), n n
x
g(x)
d
dt
div g x, y
Geodesic Active Contours, 1997
x

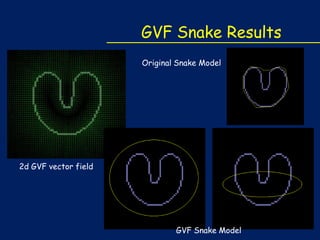
13. GVF Snakes
Replace the external force with gradient vector flow (GVF) force v.
dC
dt
C pp
C pppp
g C
V(x,y) = [u(x,y),v(x,y)]
Why?
f generally have large magnitudes only in the vicinity of the edges, the
capture range would be small.
It’s nearly zero in homogeneous regions.
V(x,y) = [u(x,y), v(x,y)] is defined as the vector field that minimizes
the energy functional:
http://www.iacl.ece.jhu.edu/static/gvf/

14. GVF Snake Results
Original Snake Model
2d GVF vector field
GVF Snake Model

15. itk Implementation for
GVF Geodesic Active Contour
Original Image
Gradient Magnitude
Gradient
Initial Contour
Sigmoid
Rescaling
Geodesic
Active
Contour
Gradient
Vector Flow
Thresholding
Insight Segmentation and Registration Toolkit (ITK)

16. itk Implementation for
GVF Geodesic Active Contour
gvfFilter->Update();
GeoAC->SetInput(initialContour->GetOutput());
GeoAC->SetAutoGenerateSpeedAdvection(false);
GeoAC->SetFeatureImage(sigmoid->GetOutput());
GeoAC->GenerateSpeedImage();
GeoAC->SetAdvectionImage(gvfFilter->GetOutput());

17. Recommended:
Numerical Geometry of Images:
http://webcourse.cs.technion.ac.il/236861/Winter2012-2013/en/ho_Tutorials.html

18. Calculus of Variations
Generalization of Calculus that seeks to find the
path, curve, surface, etc., for which a given Functional has
a minimum or maximum.
Goal: find extrema values of integrals of the form
F (u, u x )dx
It has an extremum only if the Euler-Lagrange
Differential Equation is satisfied,
u
d
F ( u, u x )
dx u x
0

19. Calculus of Variations
Example: Find the shape of the curve {x,y(x)} with
shortest length:
x1
y ( x1 )
2
1 y x dx ,
y ( x0 )
x0
given y(x0),y(x1)
x0
Solution: a differential equation that y(x) must
satisfy,
y xx
0
yx a
y ( x ) ax b
3/ 2
2
1 yx
x1