Downloaded 29 times
Uploaded byYan Xu
Linear algebra and probability (Deep Learning chapter 2&3)
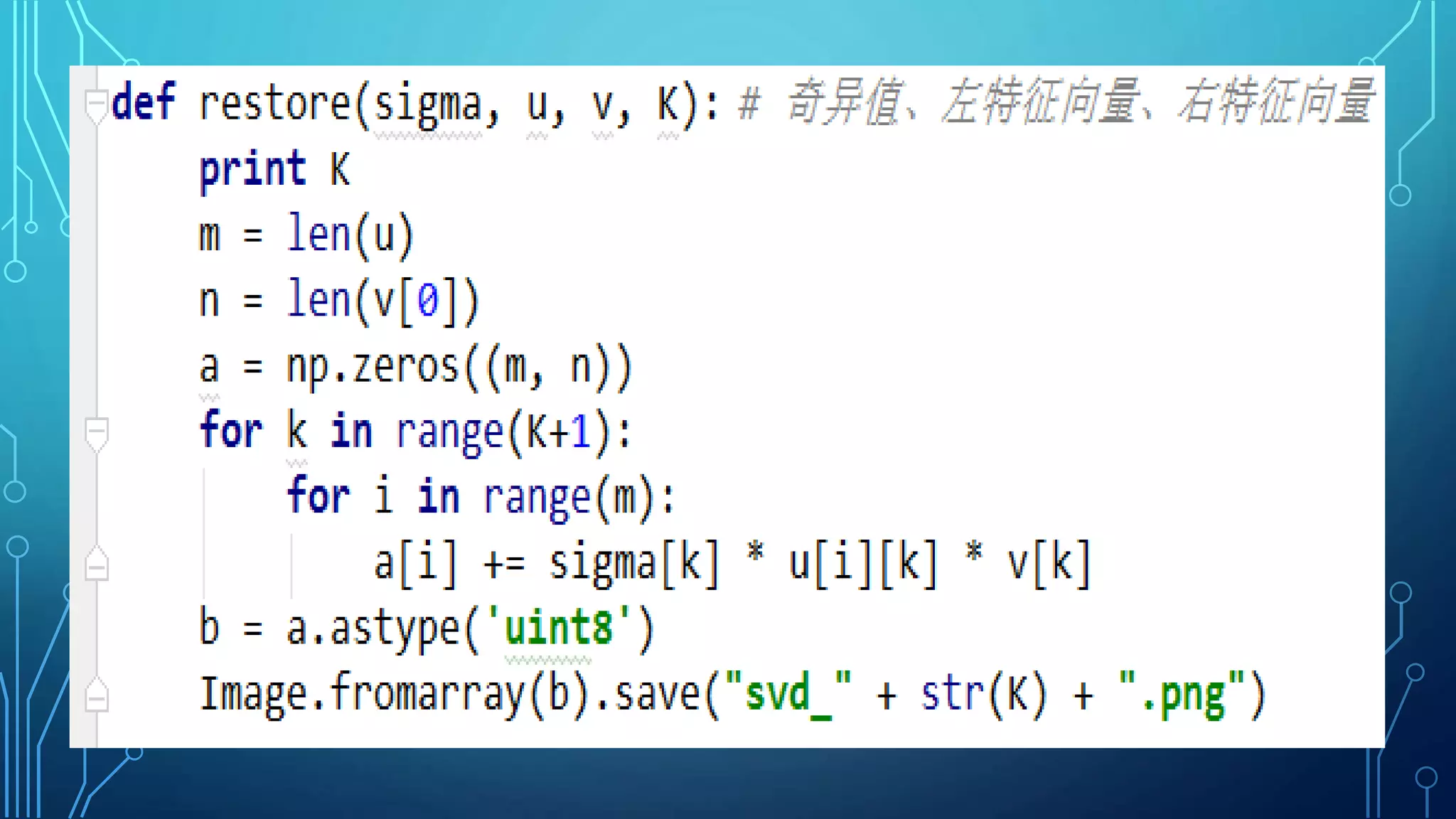
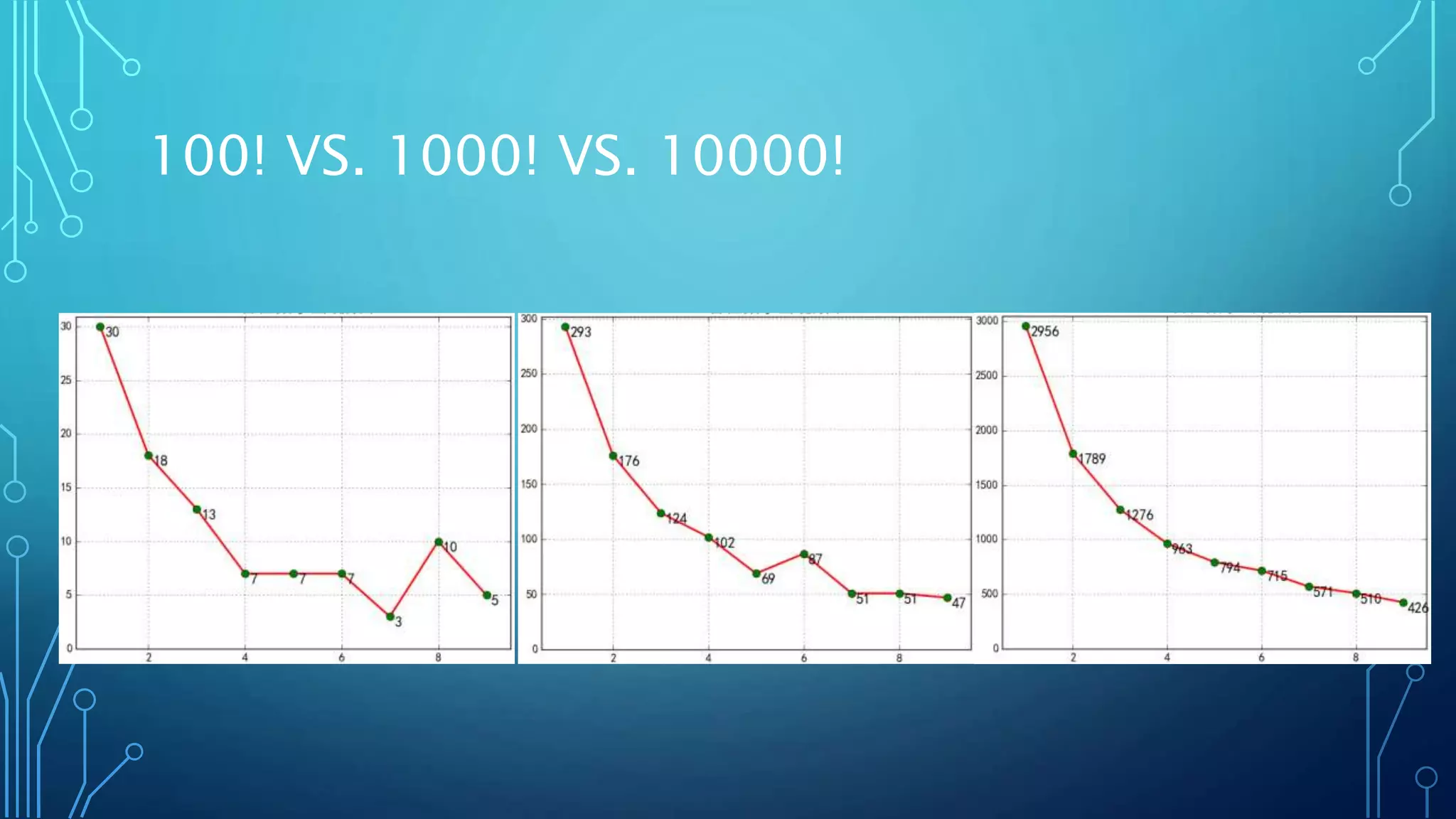
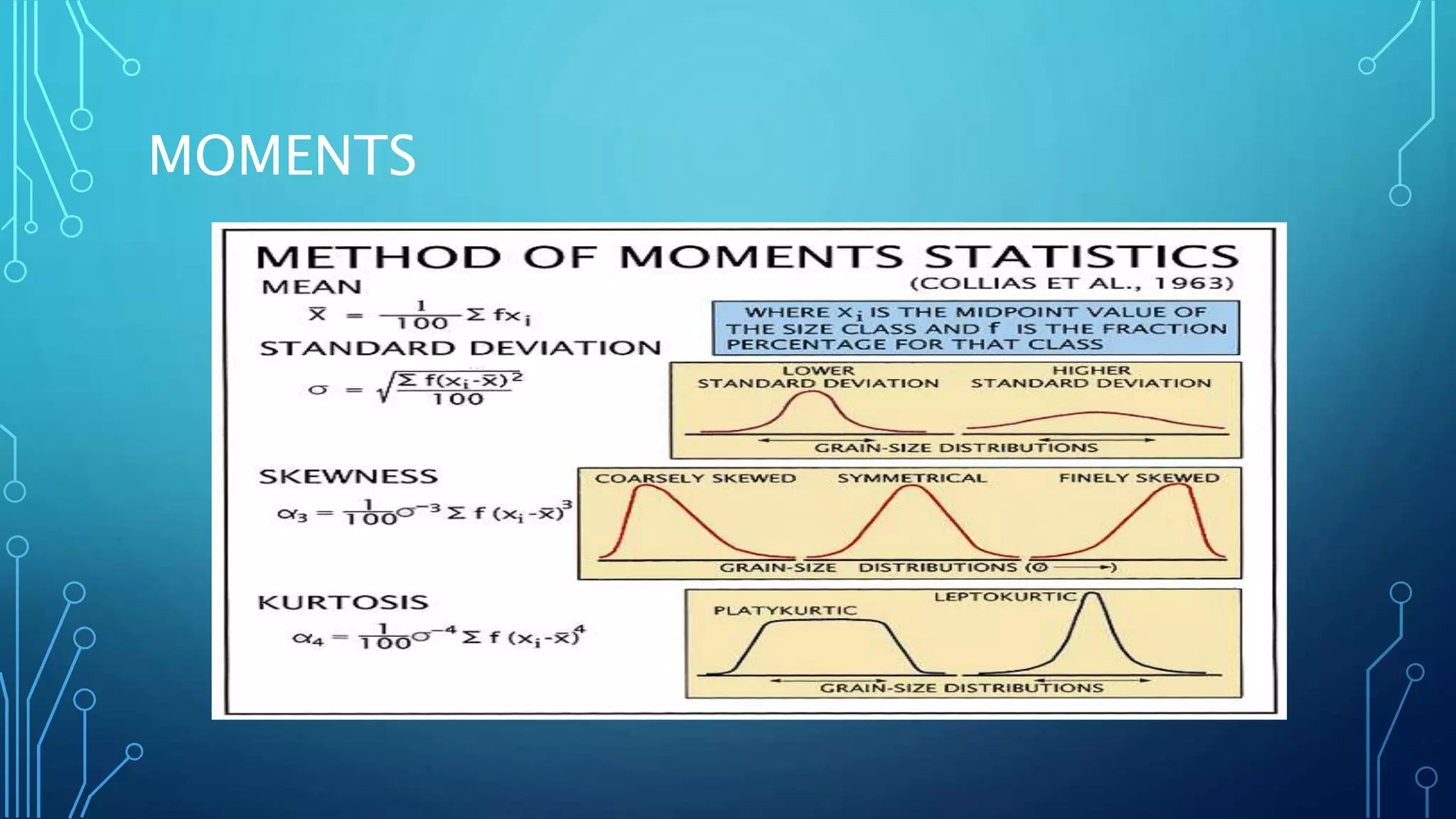
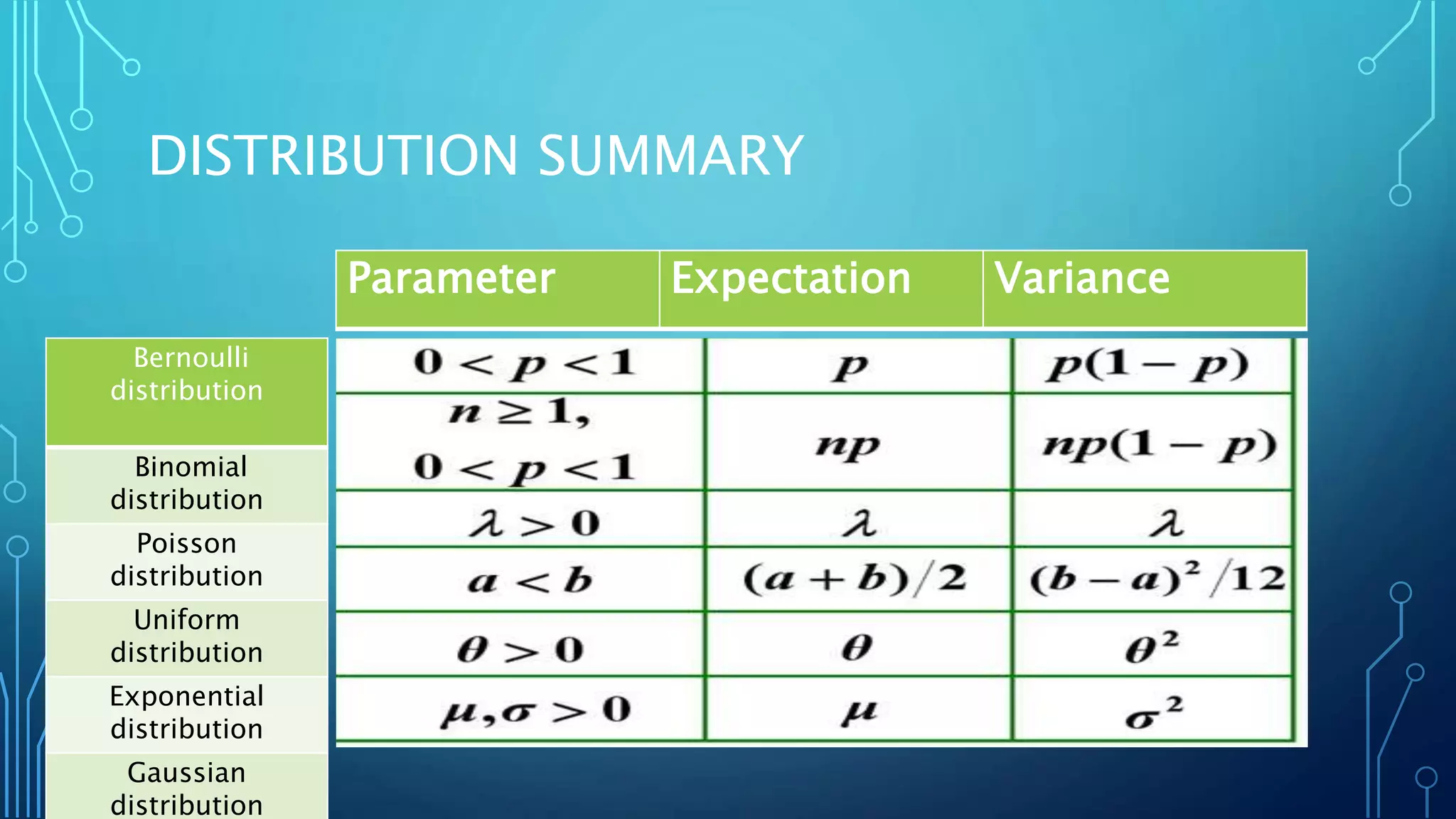
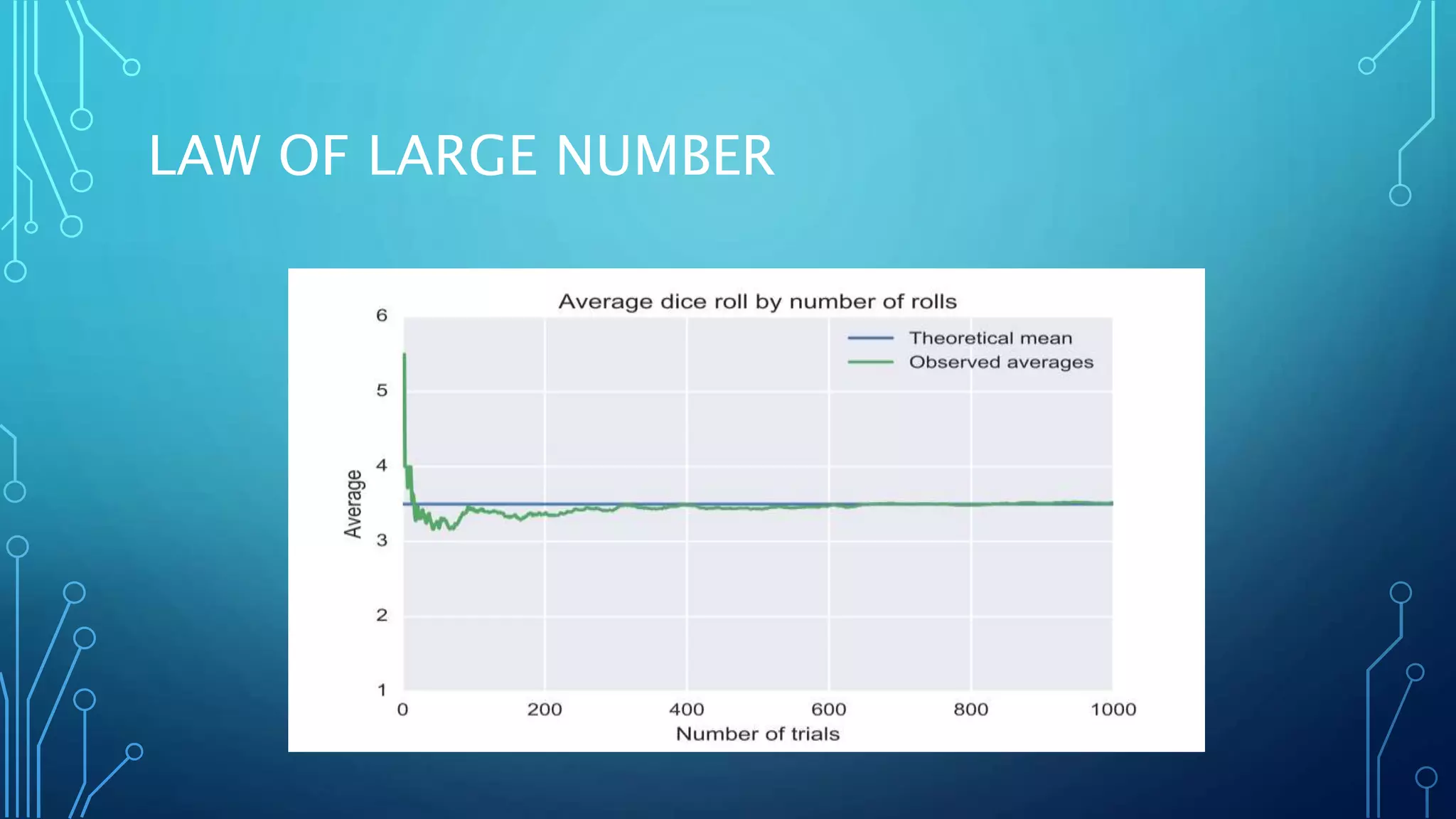
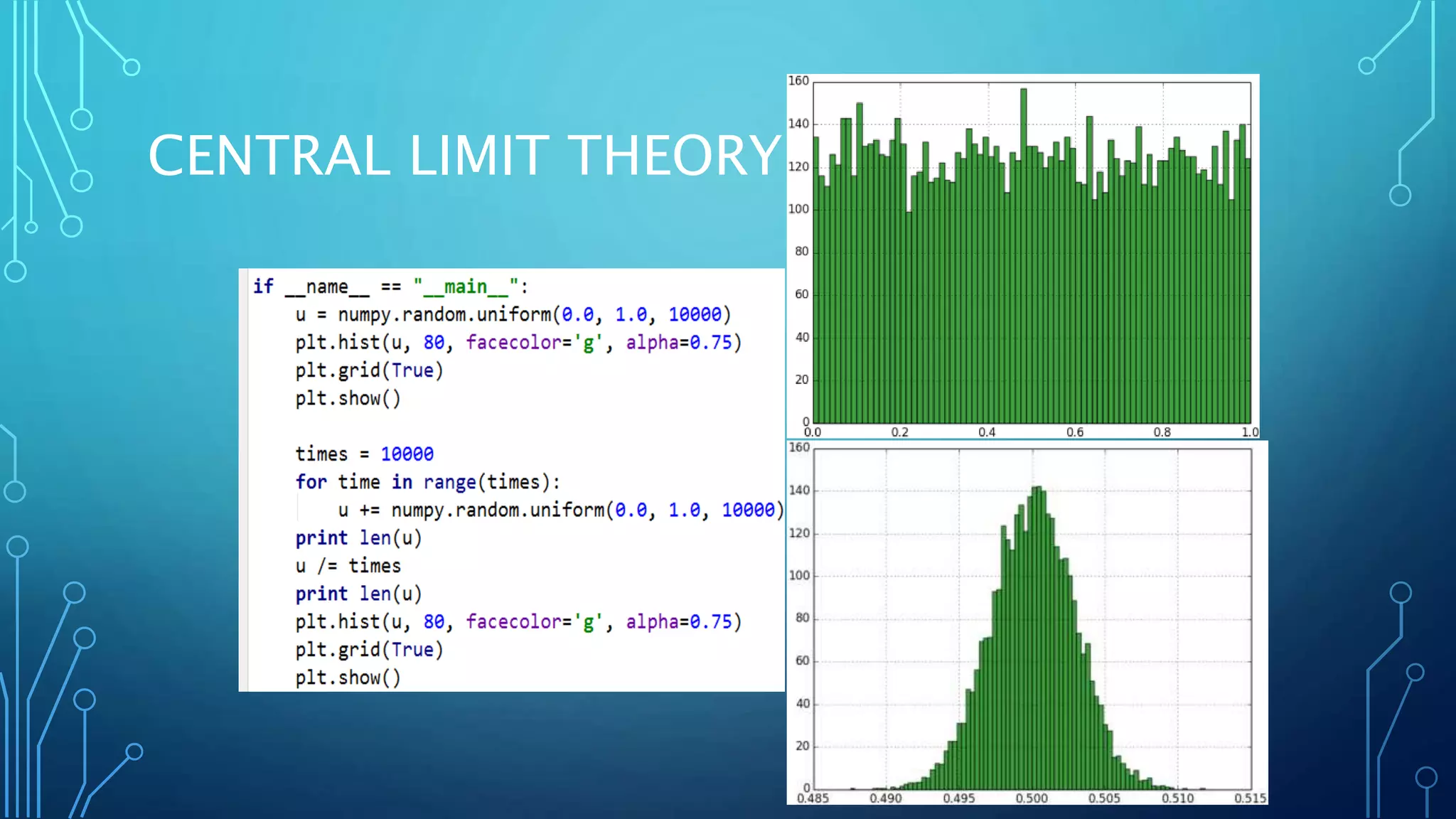
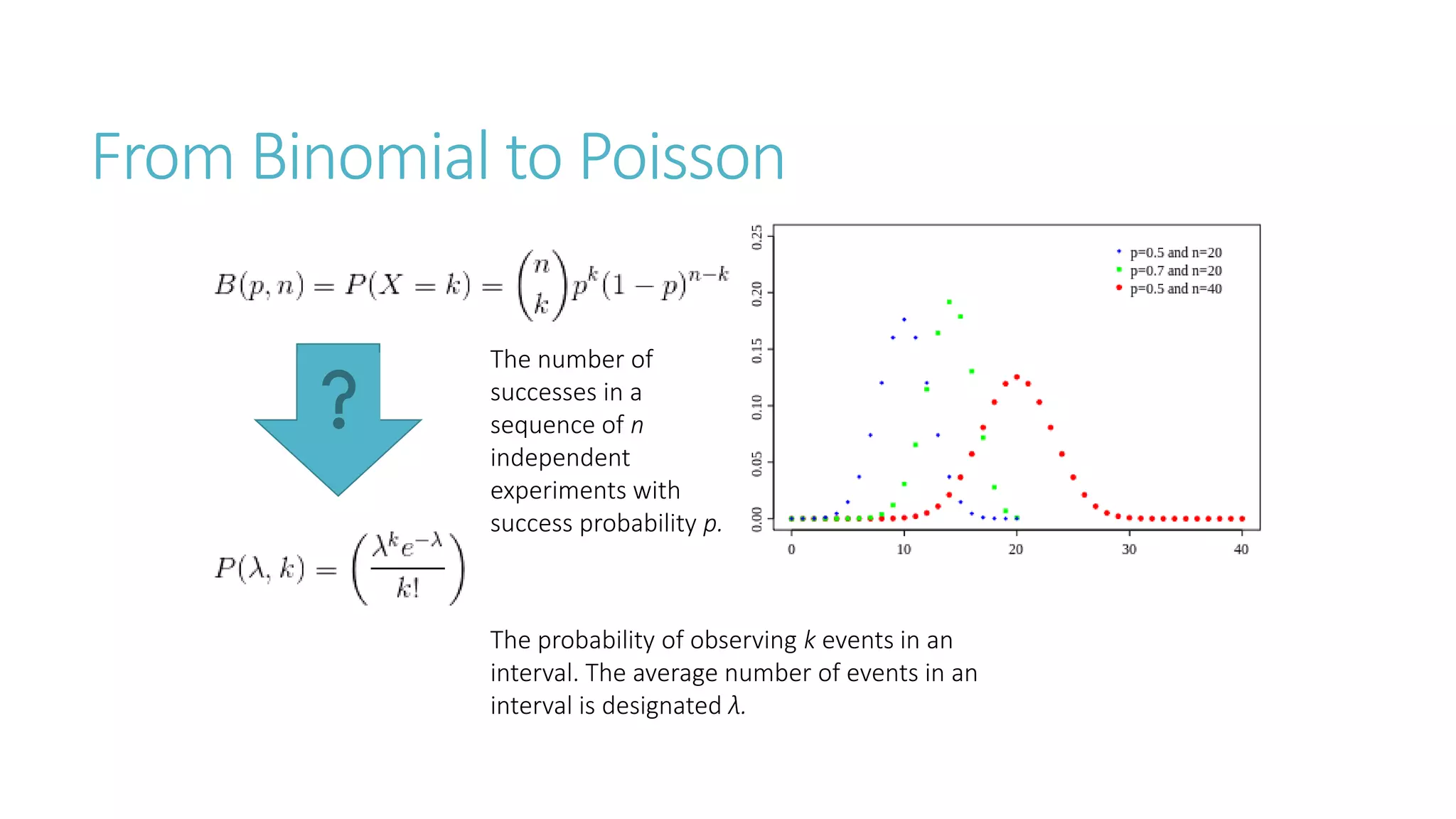
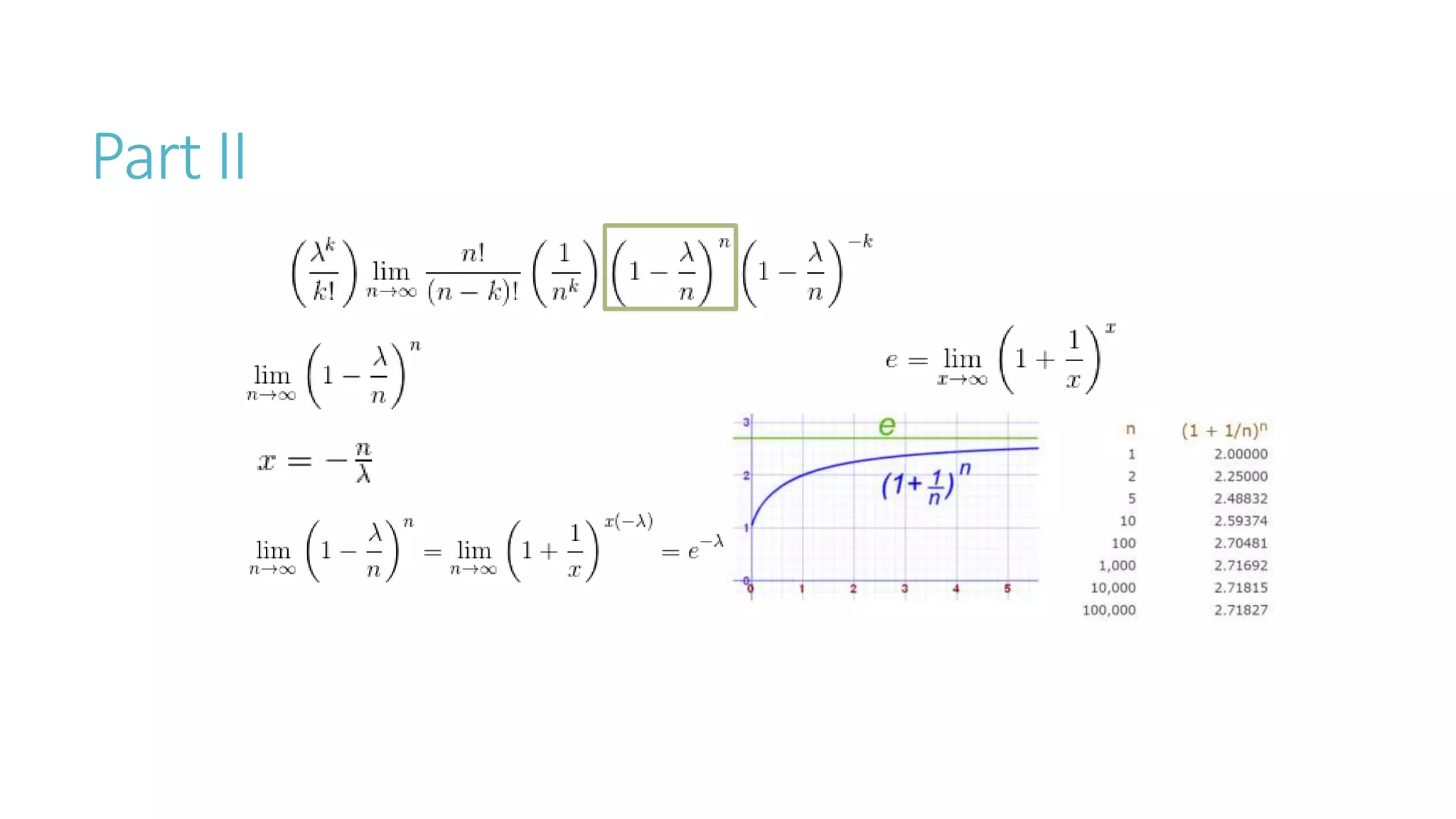
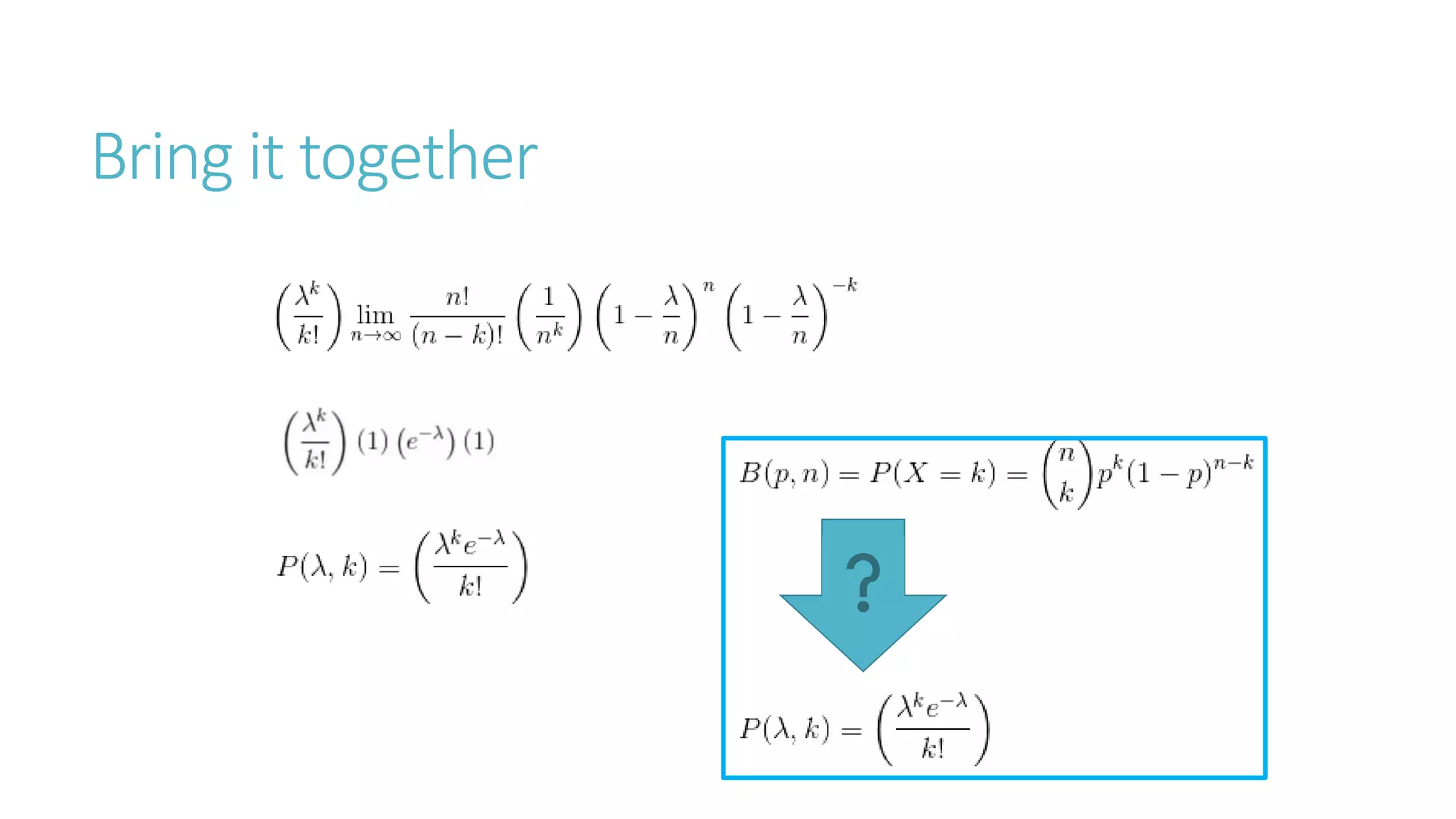
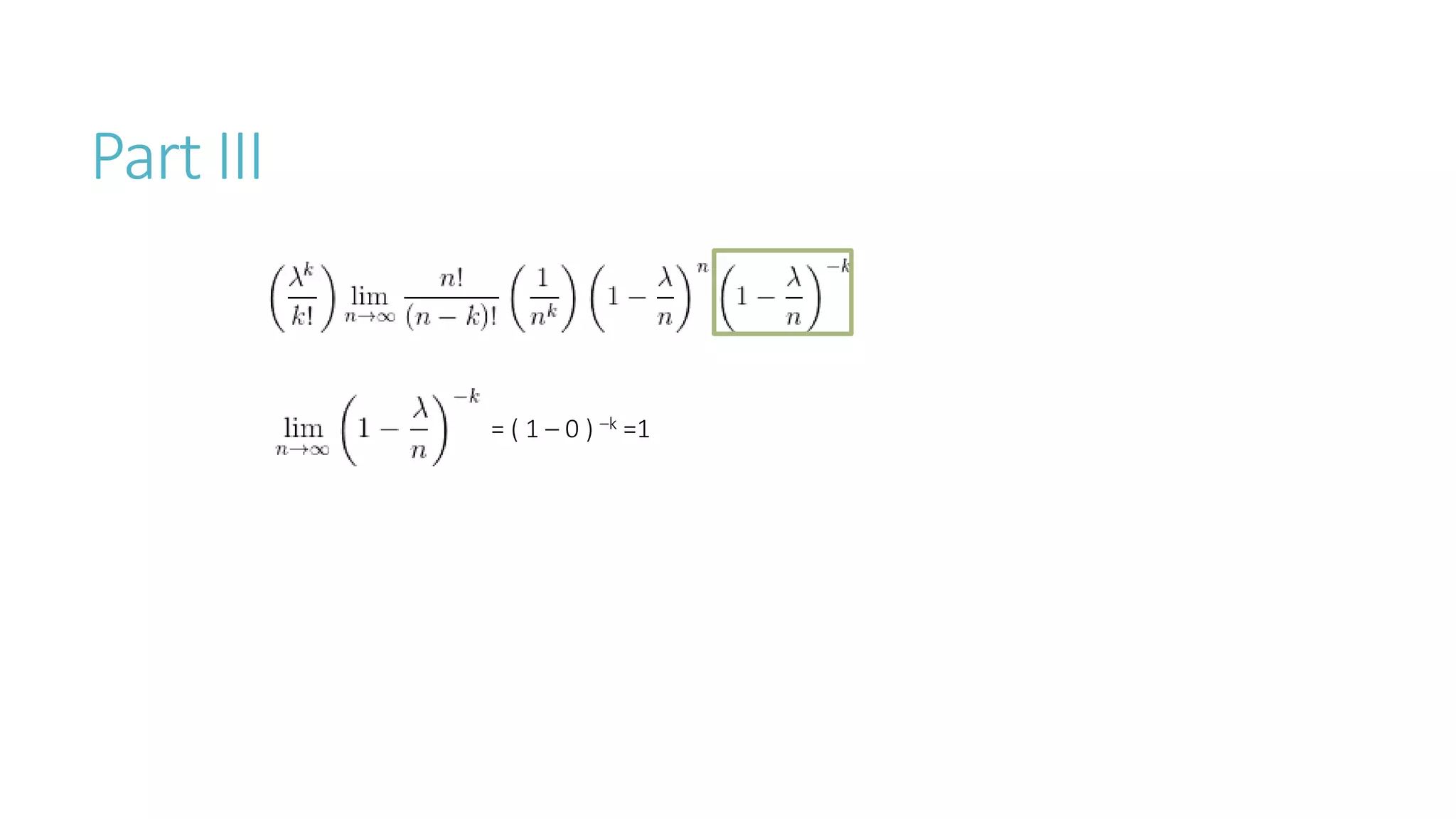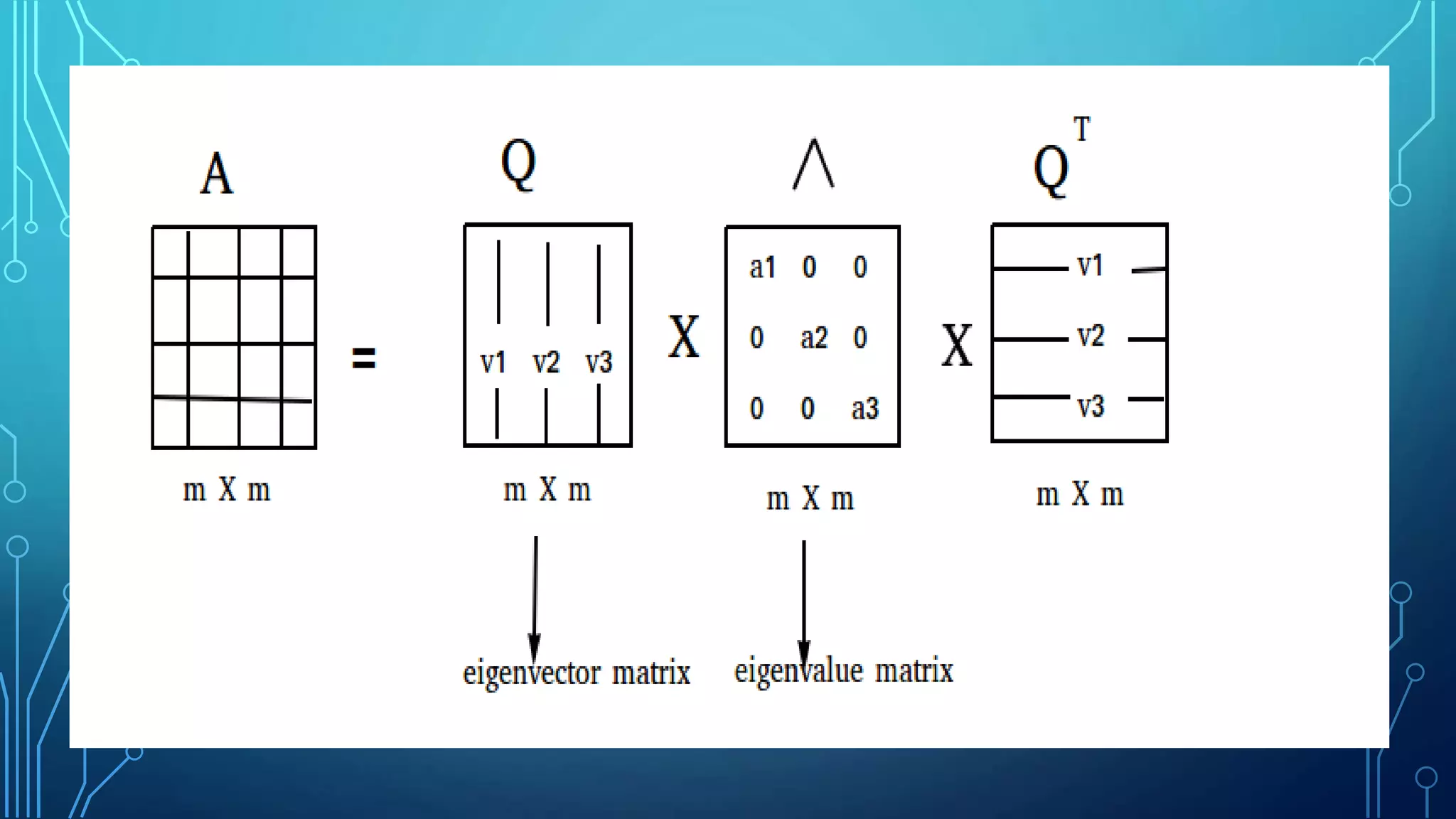
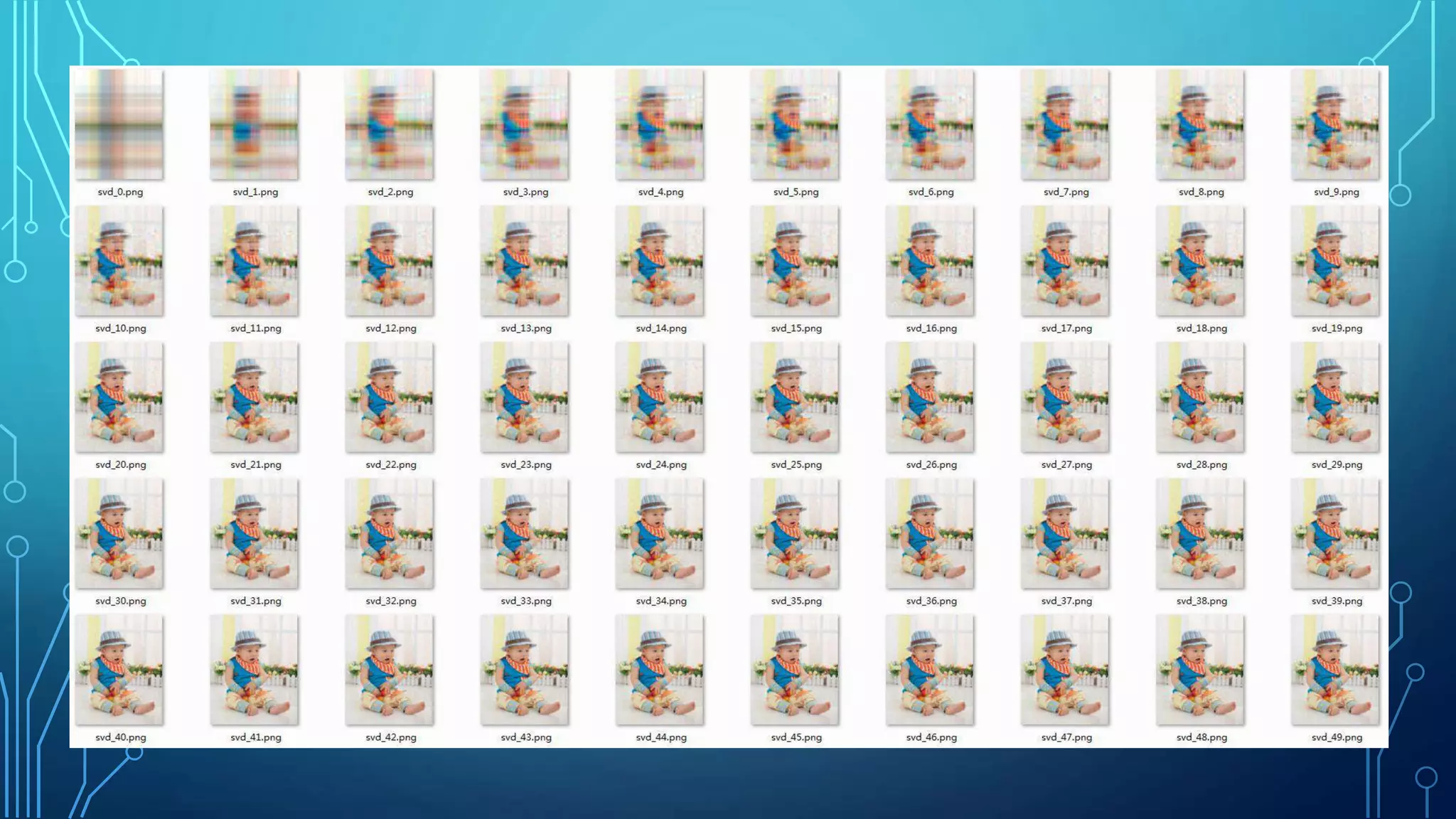
Linear algebra and probability concepts are summarized in 3 sentences: Scalars, vectors, matrices, and tensors are introduced as the basic components of linear algebra. Common linear algebra operations like transpose, addition, and multiplication are described. Probability concepts such as random variables, probability distributions, moments, and the central limit theorem are covered to lay the foundation for understanding deep learning techniques.
More Related Content
Similar to Linear algebra and probability (Deep Learning chapter 2&3)
Linear algebra and probability (Deep Learning chapter 2&3)
- 1. LINEAR ALGEBRA AND PROBABILITY(DEEP LEARNING CHAPTER 2&3) CHENG ZHAN YAN XU
- 4. SCALARS, VECTORS, MATRICESAND TENSORS • Scalars: A scalar is just a single number • Vectors: A vector is an array of numbers • Matrices: A matrix is a 2-D array of numbers • Tensors: An array of numbers arranged on a regular grid with a variable number of axes is known as a tensor
- 5. OPERATION • Transpose • Addition •In the context of deep learning, we also use some less conventional notation. We allow the addition of matrix and a vector, yielding another matrix: C = A +b • Multiplication • A(B + C) = AB + AC • A(BC) = (AB)C • AB = BA does not always hold, unlike scalar multiplication
- 6. APPLICATION OF MATRIXMULTIPLICATION
- 7. IDENTITY AND INVERSEMATRICES • Ax=b • Identity matrix • When the inverse exists, several different algorithms can find it • Gaussian elimination leads to O(n^3) complexity • Iterative method, like gradient descent (steepest descent) or conjugate gradient
- 8. LINEAR DEPENDENCE ANDSPAN • Ax=b, z = αx + (1 −α)y • In general, this kind of operation is called a linear combination • The span of a set of vectors is the set of all points obtainable by linear combination of the original vectors. • A set of vectors is linearly independent if no vector in the set is a linear combination of the other vectors.
- 9. EIGENVECTOR AND EIGENVALUE(SQUARE MATRIX)
- 15.
- 16. BENFORD'S LAW • Thefrequency distribution of leading digits in many real-life sets of numerical data is not uniform. The law states that in many naturally occurring collections of numbers, the leading significant digit is likely to be small.
- 17.
- 18. 100! VS. 1000!VS. 10000!
- 19. PROBABILITY AND INFORMATIONTHEORY • Motivation (source for uncertainty) • Inherent stochasticity in the system being modeled • Incomplete observability • Incomplete modeling • Simple over complex • Most birds fly • Birds fly, except for very young birds that have not yet learned to fly, sick or injured birds that have lost the ability to fly, flightless species of birds including the cassowary, ostrich and kiwi
- 20. • Frequentist probability •parameters are fixed • related directly to the rates at which events occur • Bayesian probability • parameters are variables that can be described by some distribution • degree of belief
- 21. RANDOM VARIABLE • Arandom variable is a variable that can take on different values randomly • A probability distribution is a description of how likely a random variable or set of random variables is to take on each of its possible states. • probability mass function (PMF) • ∀x ∈ x, 0≤ P(x)≤1, • probability density function (PDF) • ∀x ∈ x, 0≤ P(x),
- 22.
- 23.
- 24. DISTRIBUTION SUMMARY Parameter ExpectationVariance Bernoulli distribution Binomial distribution Poisson distribution Uniform distribution Exponential distribution Gaussian distribution
- 25. HOW TO DEFINETHE DISTANCE • statistical distance quantifies the distance between two statistical objects • d(x, y) ≥ 0 (non-negativity) • d(x, y) = 0 if and only if x = y (identity of indiscernible. Note that condition 1 and 2 together produce positive definiteness) • d(x, y) = d(y, x) (symmetry) • d(x, z) ≤ d(x, y) + d(y, z) (triangle inequality) • Examples • Total variation • Covariance
- 26. HOW TO DEFINETHE DISTANCE • statistical distance quantifies the distance between two statistical objects • d(x, y) ≥ 0 (non-negativity) • d(x, y) = 0 if and only if x = y (identity of indiscernible. Note that condition 1 and 2 together produce positive definiteness) • d(x, y) = d(y, x) (symmetry) • d(x, z) ≤ d(x, y) + d(y, z) (triangle inequality) • Examples • Total variation • Covariance
- 27. UNCORRELATED AND INDEPENDENT •Uncorrelated • E(XY) − E(X)E(Y) = 0 • Independent • P(X=x,Y=y)=P(X=x)P(Y=y), for all x,y.
- 28. CORRELATION AND DEPENDENCE LetX∼U(−1,1)X∼U(−1,1). Let Y = 𝑋2 . Uncorrelated but dependent.
- 29. LAW OF LARGENUMBER
- 30.
- 31. INFORMATION • A discreterandom variable x and we ask how much information is received when we observe a specific value for this variable. • Degree of surprise (there was a solar eclipse this morning) • Likely events should have low information content. • Less likely events should have higher information content. • Independent events should have additive information. • For example, finding out that a tossed coin has come up as heads twice should convey twice as much information as finding out that a tossed coin has come up as heads once.
- 33. ENTROPY • Information entropyis defined as the average amount of information produced by a stochastic source of data.
- 35. From Binomial toPoisson Yan Xu Feb. 10, 2018 Houston Machine Learning Meetup
- 36. Flipping a coin BinomialDistribution of getting heads: P(0.5, 4)
- 37. From Binomial toPoisson The number of successes in a sequence of n independent experiments with success probability p. The probability of observing k events in an interval. The average number of events in an interval is designated λ.
- 38.
- 39.
- 40.
- 41. Part III = (1 – 0 ) –k =1
- 42.
- 43. Roadmap 1. Introduction (Chapter1), Historical view and trends of deep learning – Yan Xu 2. Linear algebra and probability (Chapter 2&3) – Cheng Zhan 3. Numerical Computation and machine learning basics (Chapter 4&5) – Linda MacPhee-Cobb 4. Deep forward neural nets and regularization (Chapter 6&7) – Licheng Zhang 5 Quantum Machine Learning - Nicholas Teague 6. Optimization for training models (Chapter 8) - Zhenzhen Zhong, Yan Xu 7. Convolutional Networks (Chapter 9) – Wesley Cobb 8. Sequence modeling I (Chapter 10) 9. Sequence modeling II (Chapter 10) ......
- 44. Thank You Slides: https://www.slideshare.net/xuyangela https://www.meetup.com/Houston-Machine-Learning/ Feel freeto message me if you want to lead a session!
Editor's Notes
- #9 Determining whether Ax=b has a solution thus amounts to testing whether b is in the span of the columns of A. This particular span is known as the column space, or the range, of A
- #17 an observation about the
- #20 Mathematical framework for representing uncertain statements.
- #21 drawing a certain hand of cards in a poker game If a doctor analyzes a patient and says that the patient has a 40 percent chance of having the flu
- #24 In many cases, we are interested in the probability of some event, given that some other event has happened.
- #33 A message saying “the sun rose this morning” is so uninformative as to be unnecessary to send, but a message saying “there was a solar eclipse this morning” is very informative. and in the extreme case, events that are guaranteed to happen should have no information content whatsoever. We begin by considering a discrete random variable x and we ask how much information is received when we observe a specific value for this variable. The amount of information can be viewed as the ‘degree of surprise’ on learning the value of x.