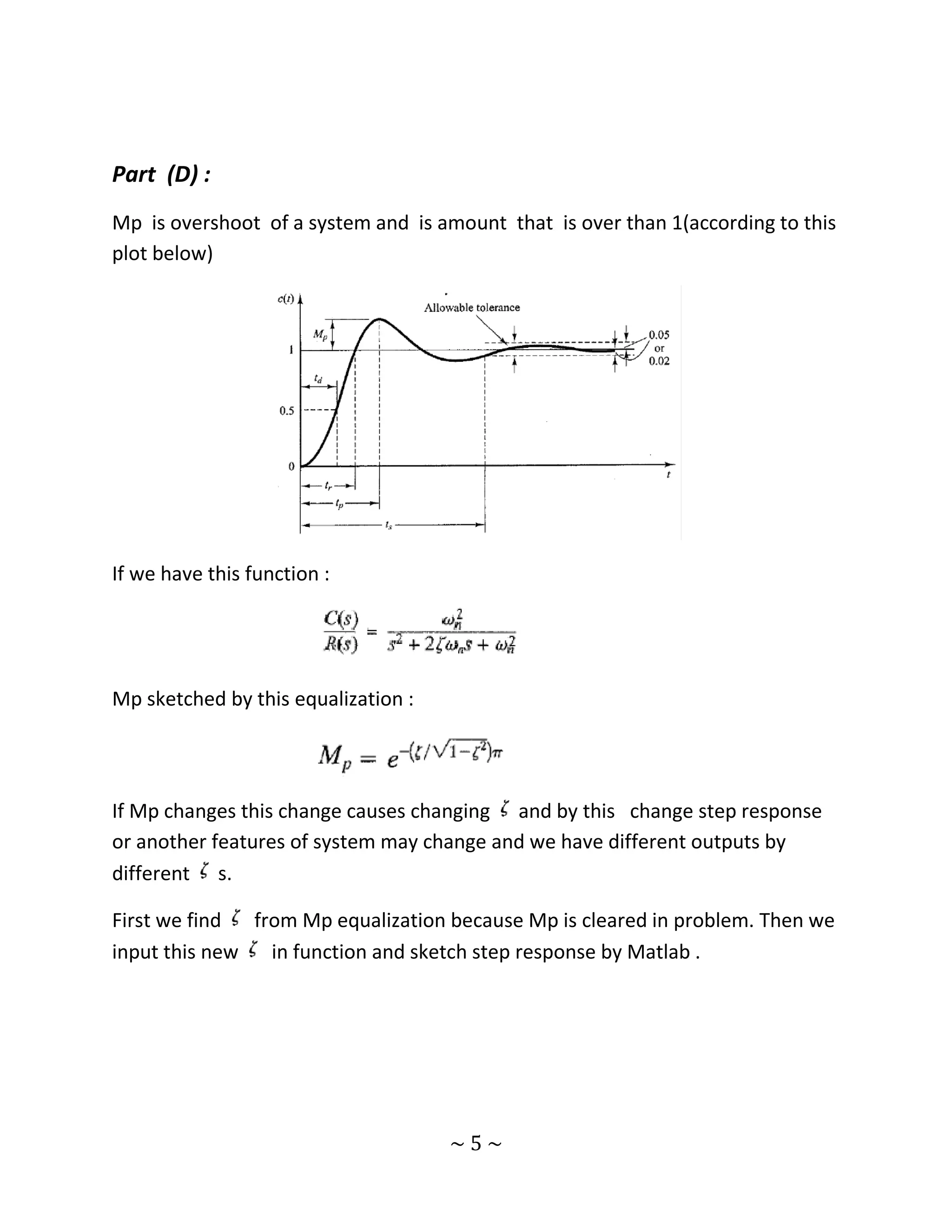
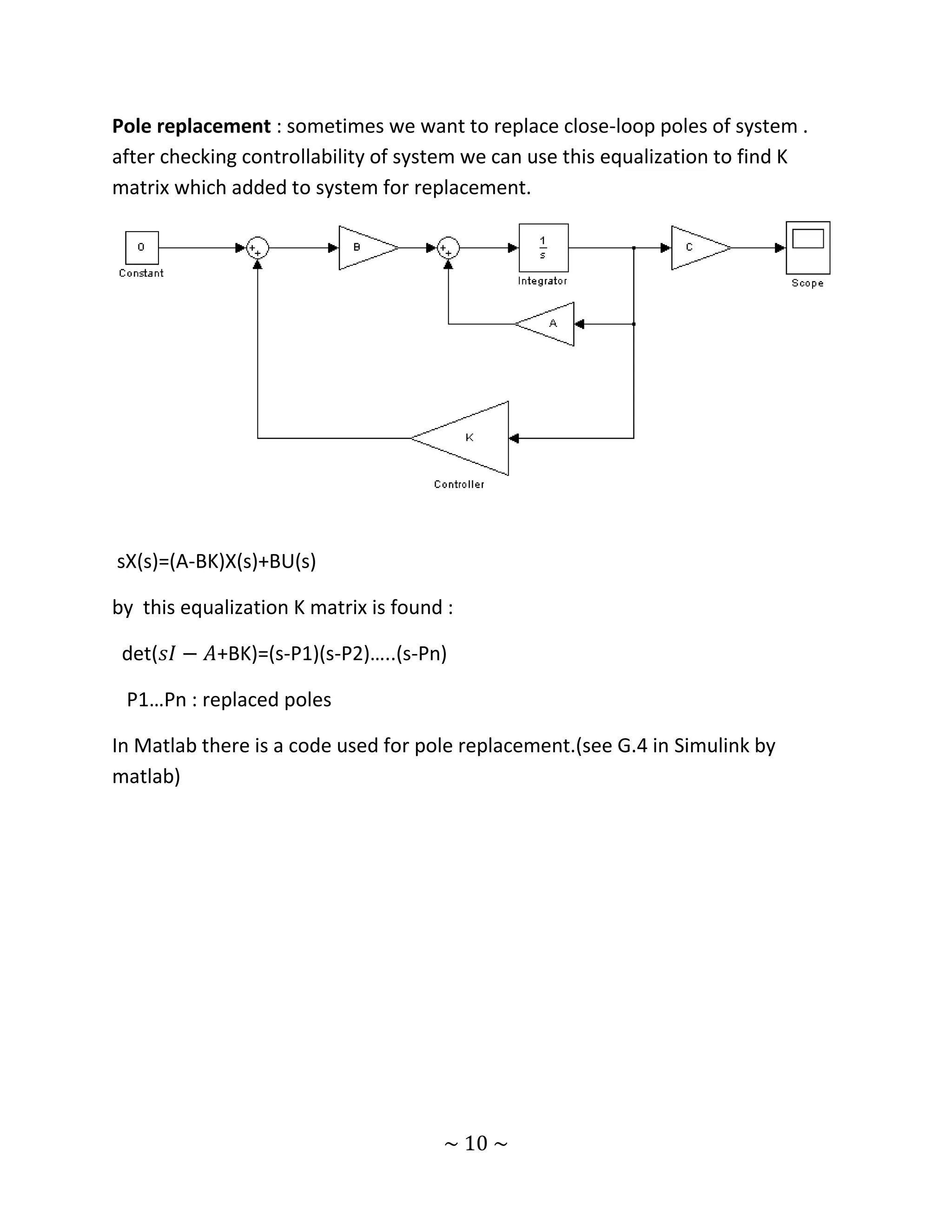
The document presents a detailed final project report from the University of Zanjan's Electrical Engineering Department focused on designing a control system using MATLAB and Simulink. It covers various aspects such as mathematical problem-solving, system response analysis, compensator design, and state-space representation, followed by detailed MATLAB code for simulations. The report includes numerous plots, like pole-zero maps and response graphs, to illustrate results and validate the effectiveness of the proposed control solutions.

1. In The Name Of God
University Of Zanjan
Electrical engineering department
Leanier systems control
Final project
Lecturer: Dr Farhad Bayat
Students :
Alireza Mirzaei 88442176
Mahyar Seyedan 88442141
Fall- 2011
~1~

2. Content :
Intruduction ………………………………………………………. (3)
Way of solving…………………………………………………...(3)
Simulink by matlab…………………………………………….(11)
Plots………………………………………………………………….(15)
Answers…………………………………………………………..(26)
~2~

3. Introduction :
In this project we are trying to show steps of designing of a system.in all steps we
have some problems and we want to solve all the problems in order to can say
this system is reliable.because of that in this project’s used Matlab to show the
result of each step and simulink parts of this system.
Way of solving :
In this part ,mathmatical way of solving each part has offered.In some of them
maybe you have another way to reach the result but these ways’re recommanded
and we use this ways in matlab.
Part(A)
Poles & Zeroes:
𝐴(𝑠)
Example: Y(s)=
𝐵(𝑠)
Zeroes of Y(s) : roots of A(s)
Poles of Y(s) : roots of B(s)
When poles & zeroes of system sketched , we can write Y(s) in this form :
K s−z0 s−z1 s−z2 ….. s−Zn
Y(s)=
s−P0 s−P1 s−P2 s−P3 ….. s−Pn
Notice : K is real number that sketched when we take apart Y(s) to some (s-Pn)
form.
~3~

4. Approximating Y(s) :
We can decrease order of Y(s) by removing (s-Pn) or (s-Zn) forms of Y(s) to reach
your order. We can’t remove every poles or zeroes we want , but we choose
poles and zeroes which aren’t more effective on output of a system . These poles
are farther than other poles from Image axis and zeroes are near undeleted poles.
Notice : when a pole or zero got rid of a function ,we should put its effect in
steady state means for example effect of (s-P0) in steady state is (-P0).
Part (B) :
Step response means input of a system is a step signal and we want to know
output of system by this input . Impulse response means input of a system is
impulse .impulse is a signal that just have one infinite value in very short time and
then became zero.
This part simulinked by Matlab.
Part (C) :
Kp = lim GH(s)
𝑠→0
Ess means steady state error and when we use Kp for finding Ess when we want
to find steady state error for step input .Kp is called position error coefficient . Ess
Sketched by :
1
Ess =
1+𝐾𝑝
root locus is plot of roots when K(gain of Y(s)) changes from minus infinite to
positive infinite.
We find that by Matlab.
~4~

5. Part (D) :
Mp is overshoot of a system and is amount that is over than 1(according to this
plot below)
If we have this function :
Mp sketched by this equalization :
If Mp changes this change causes changing and by this change step response
or another features of system may change and we have different outputs by
different s.
First we find from Mp equalization because Mp is cleared in problem. Then we
input this new in function and sketch step response by Matlab .
~5~

6. Part (E) :
Nyquist :
If in general function (open loop) s=jw we can plot function by its size and angle
when w changes from minus infinite to positive infinite . in control we called this
plot Nyquist plot. By Nyquist plot we can find phase margin and gain margin and
some better information for analysis of a system.
for Example :
We sketch Nyquist plot of our aproximated function by Matlab.
Part (F) :
Frequency Analysis :
Sometimes we want to control a system and decrease steady state error or
increase stability condition of that. we should design a function which called
compensator to reach that condition. Compensator multiple to open-loop
function and changes stability condition or steady state error.
There are two kind of Compensator :
1.Lead Compensator : increase stability condition
2.Lag Compensator : decrease steady state error
Notice : sometimes both of them used for better result.
~6~

7. This are steps of designing :
1.Lead Compensator :
a) sketch the new poles with new condition
P1=- Wn+jWn 1 − ^2
P2=- Wn-jWn 1 − ^2
b) choose one of the new poles and find vector of old poles and that new poles :
a=Pold1-P1
b=Pold2-P1
c) find angel that in need to reach new condition
ph=180-(180-∟a)-(180-∟b)
1
d) finding &α
𝑇
𝑦𝑃 1
B=180-arctan(| |);
𝑥𝑃1
𝑝ℎ +𝐵
M1=tan ( )
2
𝐵−𝑝ℎ
M2=tan ( )
2
1 𝑦𝑃1
- = 𝑥𝑃1-
𝑇 𝑀1
1 𝑦𝑃1
- = 𝑥𝑃1-
𝛼𝑇 𝑀1
~7~

8. e) check this equalization to find Kc :
1
𝑠+
𝑇
if s=P1 |Kc 1 G(s)|=1
𝑠+
𝛼𝑇
1
𝑠+
𝑇
f) Lead Compensator : Gclead(s)= Kc 1
𝑠+
𝛼𝑇
2.Lag Compensator :
a) A2 : Compensated gain & A1 : Uncompensated gain
𝐴2
=β
𝐴1
b) solve this equalization to find T :
1
𝑠+
𝑇
if s=P1 | 1 |=1
𝑠+
β 𝑇
1
𝑠+
𝑇
-5 ˂ ∟ 1 ≤0
𝑠+
β 𝑇
e) check this equalization to find Kc :
1
𝑠+
𝑇
if s=P1 | Kc 1 G(s) |=1
𝑠+
β 𝑇
1
𝑠+
𝑇
c) Lag Compensator : Gclag(s)= Kc 1
𝑠+
β 𝑇
after designing both of them open-loop function will be :
Gc(s)= Gclead(s)G(s)Gclag(s)
~8~

9. Part (G) :
In state space a system defined by this matrixes :
X : state vector (n x 1)
U : input vector (m x 1)
Y : output vector (p x 1)
A : system matrix (n x n)
B : system input matrix (n x m)
C : output matrix (p x n)
D : input matrix ,usually for SISO systems is 0
When this matrixes go into state space :
sX(s)=AX(s)+BU(s)
Y(s)=CX(s)+DU(s)
If these equalization solved :
X(s)=(𝑠𝐼 − 𝐴)−1 BU(s)
G(s)=C(𝑠𝐼 − 𝐴)−1 B+D
Roots of det(𝑠𝐼 − 𝐴 ) will be Poles of G(s) .
We can check controllability of system by this way :
Q=[ B AB 𝐴2 B …… 𝐴 𝑛 −1 B]
If rank(Q)=n : system is controllable
Otherwise : system is uncontrollable
~9~

10. Pole replacement : sometimes we want to replace close-loop poles of system .
after checking controllability of system we can use this equalization to find K
matrix which added to system for replacement.
sX(s)=(A-BK)X(s)+BU(s)
by this equalization K matrix is found :
det(𝑠𝐼 − 𝐴+BK)=(s-P1)(s-P2)…..(s-Pn)
P1…Pn : replaced poles
In Matlab there is a code used for pole replacement.(see G.4 in Simulink by
matlab)
~ 10 ~

11. Simulink by Matlab :
%part A
N=[1 112/25 48/25];
D=[1 23/2 25 93/4 27/4];
G=tf(N,D);
p=pole(G);
z=zero(G);
g=zpk(G);
N1=[1 4];
D1=[1 2 1.5];
k1=polyval(N,0)/polyval(D,0);
k2=polyval(N1,0)/polyval(D1,0);
k3=(k1/k2);
N1=N1*k3;
G1=tf(N1,D1);
g1=zpk(G1);
figure
pzmap(G);
figure
pzmap(G1);
%----------------------------------------------------------
--
%PART B
figure
step(G1,G,'--');
grid;
figure
impulse(G1,G,'--');
grid;
%----------------------------------------------------------
--
%PART C
Kpgeneral=polyval(N,0)/polyval(D,0);
~ 11 ~

12. G2=Kpgeneral*G;
G2=feedback(G2,1);
Kpapx=polyval(N1,0)/polyval(D1,0);
G1apx=Kpapx*G1;
G1apx=feedback(G1apx,1);
figure
rlocus(G2);
figure
rlocus(G1apx);
[Gm,Pm,Wg,Wp] = margin(G1apx);
%----------------------------------------------------------
-
%PART D
[Nsys,Dsys]=feedback(N1,D1,1,1);
sysz1=tf(Nsys,Dsys);
Wncl=sqrt(Dsys(3));
zitasys=Dsys(2)/(2*Wncl);
zitasysmax=1/abs(9+(pi)^2);
zitasysmax=sqrt(zitasysmax);
Dsys(2)=2*zitasysmax*Wncl;
Nnew=Nsys;
Dnew=Dsys-Nsys;
G1new=tf(Nnew,Dnew);
Kpnew=polyval(Nnew,0)/polyval(Dnew,0);
figure
sysnew=feedback(G1new,1);
step(sysnew,sysz1,'--');
grid;
%----------------------------------------------------------
-
%PART E
figure
nyquist(G1,G,'--');
%----------------------------------------------------------
-
~ 12 ~

13. %PART F
%F.1(lead compensator)
[numT,denT]= feedback(N1,D1,1,1);
sys=tf(numT,denT);
Wn1=sqrt(denT(3));
Wn2=2*Wn1;
zita1=denT(2)/(2*Wn1);
zita2=zita1;
p1=-(zita2*Wn2)+(Wn2*(sqrt((zita2^2)-1)));
p2=-(zita2*Wn2)-(Wn2*(sqrt((zita2^2)-1)));
p3=pole(sys);
a=p1-p3(1);
b=p1-p3(2);
ph1=pi-angle(a);
ph2=pi-angle(b);
Cph=pi-ph1-ph2;
d=pi-atan(abs((imag(p1))/real(p1)));
m1=tan((Cph+d)/2);
m2=tan((d-Cph)/2);
T=-1/(real(p1)-((imag(p1))/m1));
alpha=-T/(real(p1)-((imag(p1))/m2));
N3=[1 1/T];
D3=[1 1/(alpha*T)];
Gc=tf(N3,D3);
zpk(Gc);
Kc=1/abs((polyval(N3,p1)/polyval(D3,p1))*(polyval(N1,p1)/po
lyval(D1,p1)));
Gc=Kc*Gc;
Gcc=G1*Gc;
sys2=feedback(Gcc,1);
figure
step(sys2,sys,'--');
grid;
%F.2(lag compensator)
Kp1=polyval(N1,0)/polyval(D1,0);
Kp2=100*Kp1;
beta=Kp2/Kp1;
T2=(1-(1/(beta^2))/(-2*real(p1)*(1-(1/beta))));
N4=[1 1/T2];
D4=[1 1/(beta*T2)];
~ 13 ~

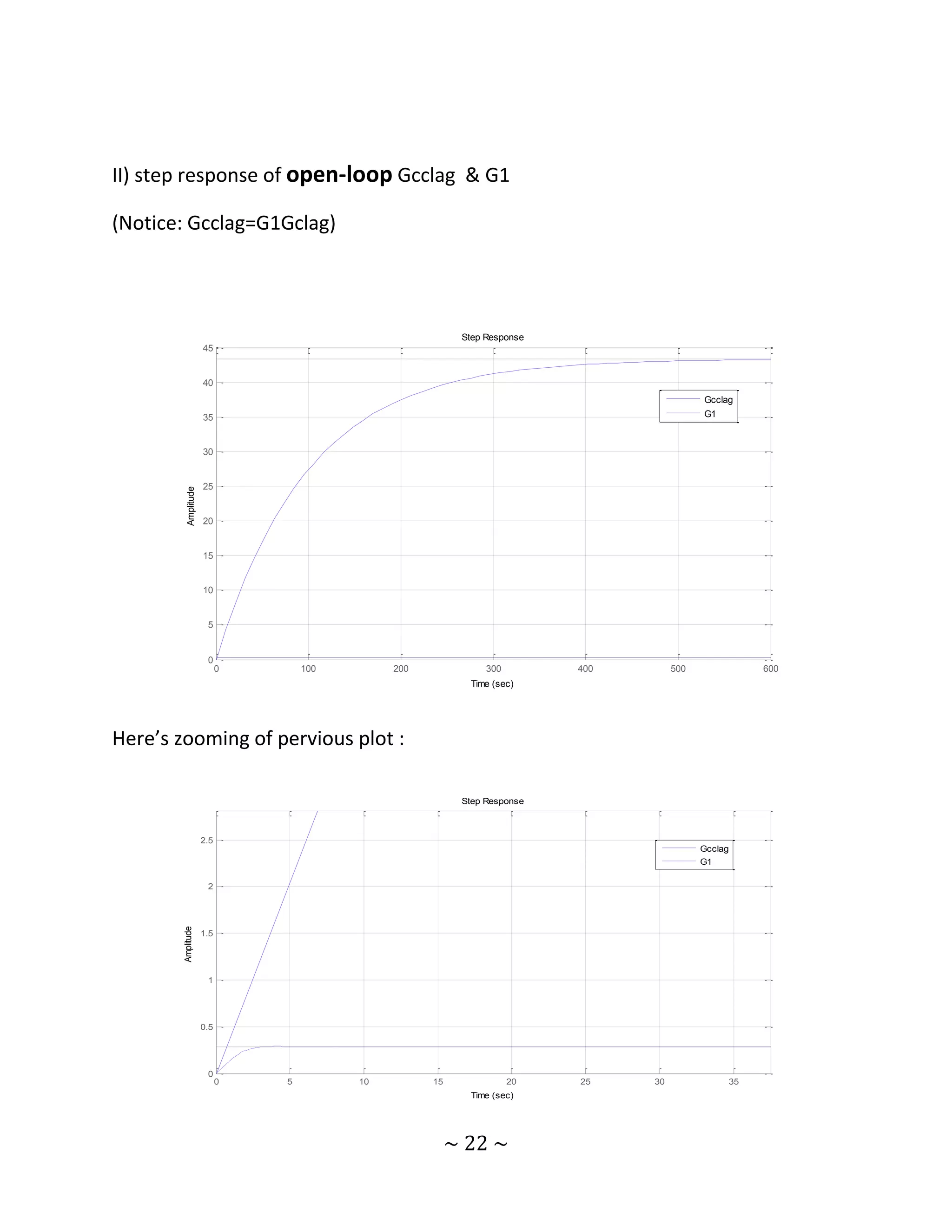
14. Gc2=tf(N4,D4);
zpk(Gc2);
Kc2=1/abs((polyval(N4,p3(1))/polyval(D4,p3(1)))*(polyval(N1
,p3(1))/polyval(D1,p3(1))));
Gc2=Kc2*Gc2;
Gcclag=Gc2*G1;
figure
step(Gcclag,G1,'--');
grid;
sys3=feedback(Gcclag,1);
figure
step(sys3,sys,'--');
grid;
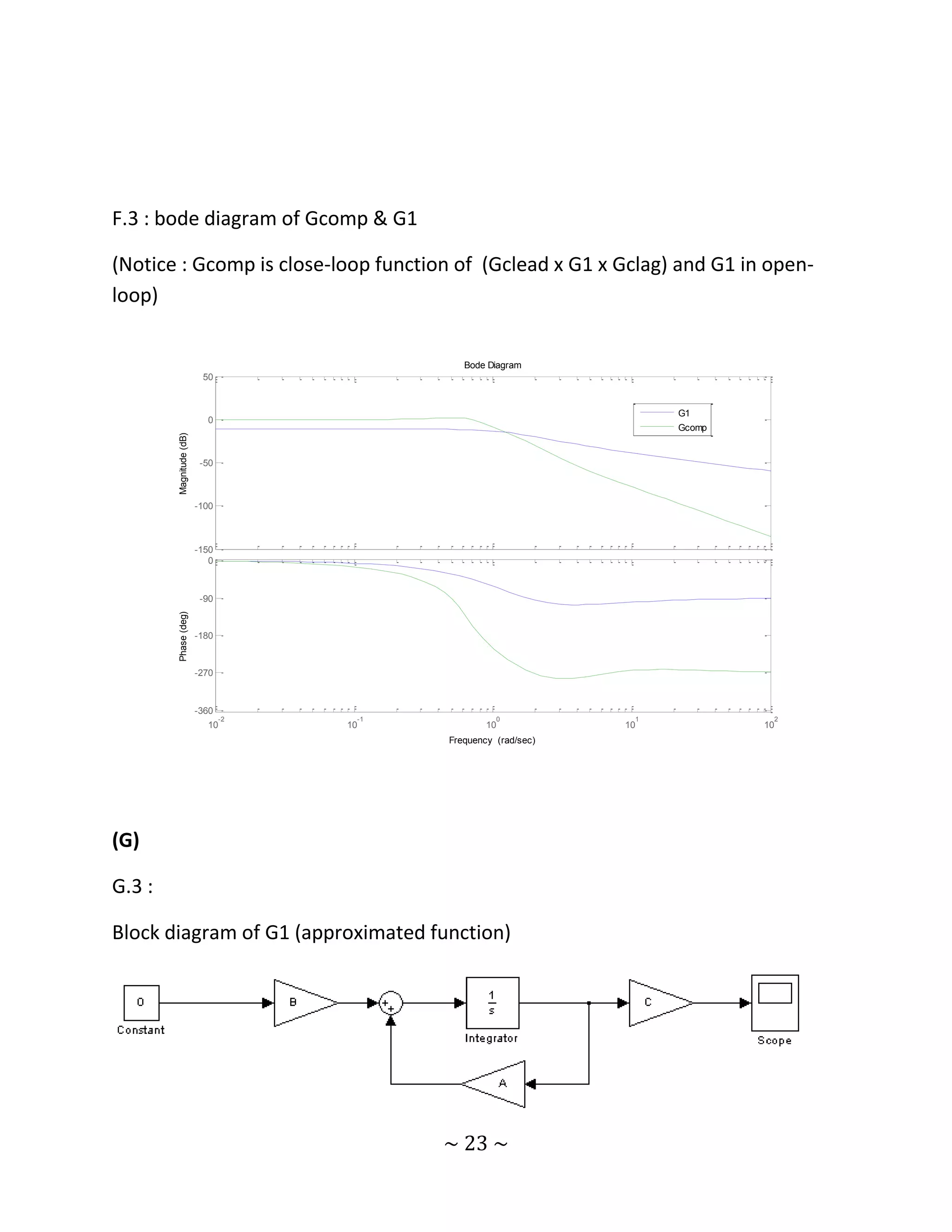
%F.3 Bode diagram
Gcomp=Gcc*G1*Gcclag;
Gcomp=feedback(Gcomp,1);
figure
bode(G1,Gcomp);
%----------------------------------------------------------
-
%PART G
%G FIND A,B,C,D STATE MATRIXS
[NF,DF]=feedback(N1,D1,1,1);
[A,B,C,D]=tf2ss(NF,DF);
%G.1 controlability check
Q=[B A*B ];
r=rank(Q);
disp(r);
%G.2
s=roots(poly(A));
s0=s(1);
s1=s(2);
%G.3 simulinked by matlab (g3.mdl in directory)
~ 14 ~

15. %G.4
sc1=2*s0;
sc2=4*s1;
J=[sc1 sc2];
K12=acker(A,B,J);
eig(A-B*K12);
disp(K12);
%G.5 simulinked by matlab (g5.mdl in directory)
sysg=ss(A-B*K12,eye(2),eye(2),eye(2));
t=0:0.01:4;
x=initial(sysg,[2;5],t);
x1=[2 5]*x';
x2=[5 2]*x';
figure
subplot(2,1,1);
plot(t,x1),grid;
subplot(2,1,2);
plot(t,x2),grid
Plots :
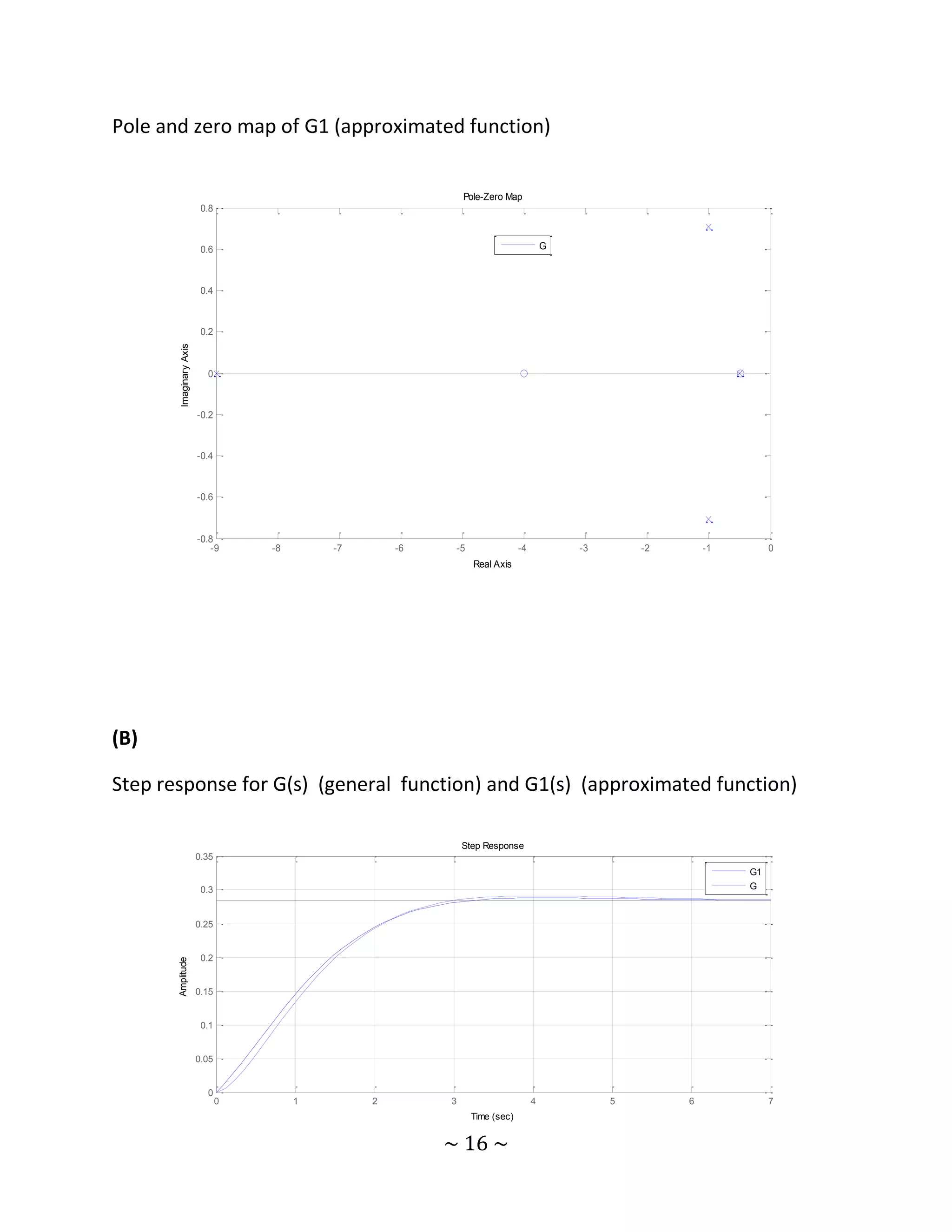
(A)
Pole zero map of G (general function)
Pole-Zero Map
0.8
0.6 G
0.4
0.2
Imaginary Axis
0
-0.2
-0.4
-0.6
-0.8
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
Real Axis
~ 15 ~

16. Pole and zero map of G1 (approximated function)
Pole-Zero Map
0.8
0.6 G
0.4
0.2
Imaginary Axis
0
-0.2
-0.4
-0.6
-0.8
-9 -8 -7 -6 -5 -4 -3 -2 -1 0
Real Axis
(B)
Step response for G(s) (general function) and G1(s) (approximated function)
Step Response
0.35
G1
0.3 G
0.25
0.2
Amplitude
0.15
0.1
0.05
0
0 1 2 3 4 5 6 7
Time (sec)
~ 16 ~

17. Impuls e response for G(s) (general function) and G1(s) (approximated function)
Impulse Response
0.16
G1
0.14 G
0.12
0.1
Amplitude
0.08
0.06
0.04
0.02
0
-0.02
0 1 2 3 4 5 6 7 8 9 10
Time (sec)
(C)
root locus of closed loop system (with G (s)*Kp in open loop)
Root Locus
25
20
15
10
5
Imaginary Axis
0
-5
-10
-15
-20
-25
-10 -8 -6 -4 -2 0 2
Real Axis
~ 17 ~

18. root locus of closed loop system (with G1 (s)*Kp in open loop)
Root Locus
4
G1apx
3
2
1
Imaginary Axis
0
-1
-2
-3
-4
-14 -12 -10 -8 -6 -4 -2 0 2
Real Axis
(D)
Step response of sysnew and sysz1
(Notice : sysnew is new G1 with of maximum overshoot less than 5% and
sysz1 before changing )
When changes overshoot of system also will change.
Step Response
0.35
sysnew
sysz1
0.3
0.25
0.2
Amplitude
0.15
0.1
0.05
0
0 2 4 6 8 10 12 14 16 18
Time (sec)
~ 18 ~

19. (E)
Nyquist diagram of G(s) (general function) and G1(s) (approximated function)
according to nyquist diagrams in low frequencies both of them absolutely
the same , and in other frequencies there is a little difference between them.
Because in low frequencies they have the same dc value.
And in high frequencies because general function is order of 2 and went to zero
By ±180 but approximated function is order of 1 and went to zero by ±90.
Nyquist Diagram
0.25
G1
0.2
G
0.15
0.1
Imaginary Axis
0.05
0
-0.05
-0.1
-0.15
-0.2
-0.25
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4
Real Axis
~ 19 ~

20. (F)
F.1 : Step response of sys2 and sys close-loops.
(notice: sys is close-loop system of approximated function without lead
compensator(Gc), but sys2 is close-loop system of compensated of G1 with lead
compensator(Gc))
We can see in this below figure lead compensator go to steady state faster and
by this steady state changes and system stability increased.
Step Response
0.8
0.7
sys2
sys
0.6
0.5
Amplitude
0.4
0.3
0.2
0.1
0
0 1 2 3 4 5 6
Time (sec)
~ 20 ~

21. F.2 :
I) step response of close-loop sys3 & sys
(Notice: sys3 is close-loop function of compensated with lag compensator and
Sys is close-loop function of G1)
We can see in this below figure steady state error decreased and output goes to
step input.
Step Response
1
0.9
sys3
0.8 sys
0.7
0.6
Amplitude
0.5
0.4
0.3
0.2
0.1
0
0 2 4 6 8 10 12 14 16 18
Time (sec)
~ 21 ~

22. II) step response of open-loop Gcclag & G1
(Notice: Gcclag=G1Gclag)
Step Response
45
40
Gcclag
35 G1
30
25
Amplitude
20
15
10
5
0
0 100 200 300 400 500 600
Time (sec)
Here’s zooming of pervious plot :
Step Response
2.5
Gcclag
G1
2
Amplitude
1.5
1
0.5
0
0 5 10 15 20 25 30 35
Time (sec)
~ 22 ~

23. F.3 : bode diagram of Gcomp & G1
(Notice : Gcomp is close-loop function of (Gclead x G1 x Gclag) and G1 in open-
loop)
Bode Diagram
50
G1
0
Gcomp
Magnitude (dB)
-50
-100
-150
0
-90
Phase (deg)
-180
-270
-360
-2 -1 0 1 2
10 10 10 10 10
Frequency (rad/sec)
(G)
G.3 :
Block diagram of G1 (approximated function)
~ 23 ~

24. initial condition of [2 5] 𝑇 (output of scope in simulink section of Matlab)
G.5 :
Block diagram of pole replaced system of G1 :
~ 24 ~

25. initial condition of [2 5] 𝑇
I) outputs by M-file section in Matlab in different periods of time
30
20
10
0
-10
0 0.5 1 1.5 2 2.5 3 3.5 4
20
10
0
-10
-20
-30
-40
0 0.5 1 1.5 2 2.5 3 3.5 4
II) output of scope in simulink section of Matlab
~ 25 ~

26. Answers:
Part (A) :
Sketch poles and zeros of system (G (s )) , then approximate G (s ) with a system
of order 2 (G~(s) )).
Answer :
𝟎.𝟏𝟎𝟔𝟕 𝒔 + 𝟎.𝟒𝟐𝟔𝟕
G~(s)=
𝐬^𝟐 + 𝟐 𝐬 + 𝟏.𝟓
Part (B) :
Sketch impulse and step response of open loop system before and after
approximation (G (s ),G% (s )).
Is your approximation acceptable?
Answer :
Yes, according to the plots of step & impulse response of G and G1 ,
approximation is acceptable because both of them are almost the same.
Part (C) :
Assume K (s) =Kp , then sketch the root locus of closed loop system for
Kp and find the range of Kp for closed loop stability.
Answer :
Kp= 0.284444444444444 gain margin= infinite
Kp<gain margin === > Kp can amounted all positive real numbers!
~ 26 ~

27. Part (D) :
Assume H (s) =1 , find Kp such that the maximum overshoot be less than 5%.
Then sketch the step response.
Answer :
Kpnew= 1.284444444444445
For step response see plots (D).
Part (E) :
(Nyquist Analysis)
E.1- Sketch the nyquist diagram for main system (G (s )) and approximated
system(G~ (s )) using MATLAB.
Note: Writing all steps are necessary for G~ (s ) .
E.2- Does the nyquist diagram of G (s ) and G~ (s ) confirm an accurate
approximation?
In which frequency two nyquist diagrams are similar and in which are
different? Why? Explain your answer?
Answers :
E.1 . see plots (E.1)
E.2 . according to nyquist diagrams in low frequencies both of them absolutely
the same , and in other frequencies there is a little difference between them.
Because in low frequencies they have the same dc value.
And in high frequencies because general function is order of 2 and went to zero
By ±180 but approximated function is order of 1 and went to zero by ±90.
Part (F) :
~ 27 ~

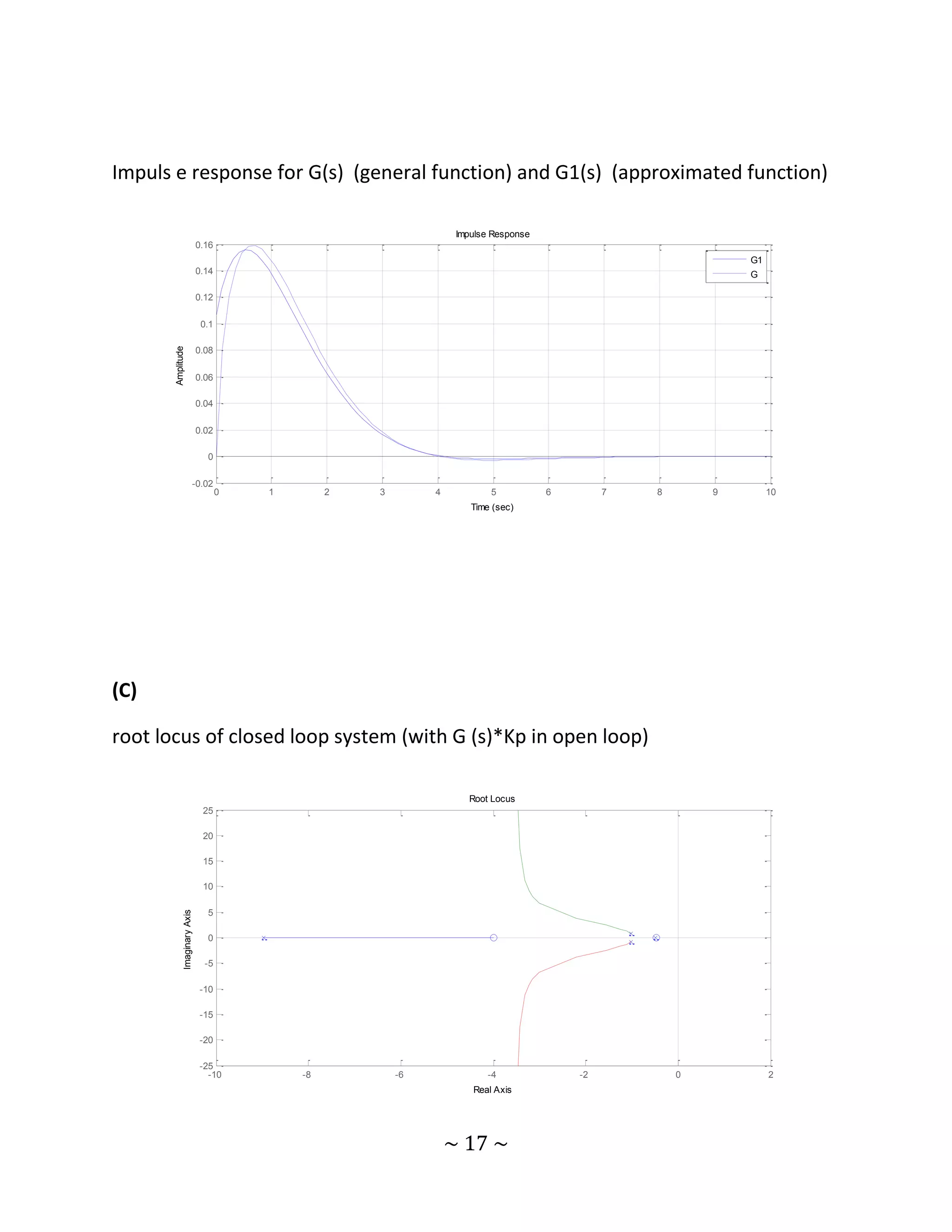
28. (Frequency Analysis)
Answers :
F.1 :
165.7 s + 786.8
Gclead(s)=
s + 36.59
F.2 :
0.1626 𝑠 2 + 0.8131 s + 0.6505
Gclag(s)=
𝑠 3 + 2.01 𝑠 2 + 1.52 s + 0.015
F.3 :
0.3066 𝑠 5 + 5.441 𝑠 4 + 37.32 𝑠 3 + 121.7 𝑠 2 + 182.7 s + 93.17
Gctotal(s)= 𝑠8 + 42.6 𝑠7 + 236.5 𝑠6 + 632.5 𝑠5 + 987.9 𝑠4 + 966.3 𝑠3 + 628.3 𝑠2 + 311.1 s+ 94.41
Part (G) :
Find a state space model (A,B ,C ,D ) for approximated
system(G~ (s)
G.1- Check the controllability of system (A,B ,C ,D ) .
G.2- Find all poles of open loop system (So1,So2 by solving det (sI -A) = 0 .
G.3- Sketch the initial condition response of open loop system forX0= [ 2 5 ] 𝑇
G.4- Let U= K.x where K=[K1 K2] , design K1 K2 such that the poles of closed loop
system place at Sc1=2So1 ,Sc2=4So2
~ 28 ~

29. G.5- Sketch the initial condition response of close loop system forX0= [2 5 ] 𝑇 .
Answers :
G.
−1.926666666666667 −1.926666666666667
A=
1 0
1
B=
0
C= [0.106666666666667 0.426666666666667]
D=0
G.1
Rank(Q)=2 and n=2 ==== > system is controllable!
G.2
So1= -1.053333333333333 + 0.903966567720044i
So2= -1.053333333333333 - 0.903966567720044i
G.3
~ 29 ~

30. See plots G.3
see and run g3.mdl in project directory
G.4
K=[K1 K2]= [4.213333333333333 13.486666666666668]
G.5
See plots G.5
see and run g5.mdl in project directory
THE END…………………………………………………………………………………………..
~ 30 ~