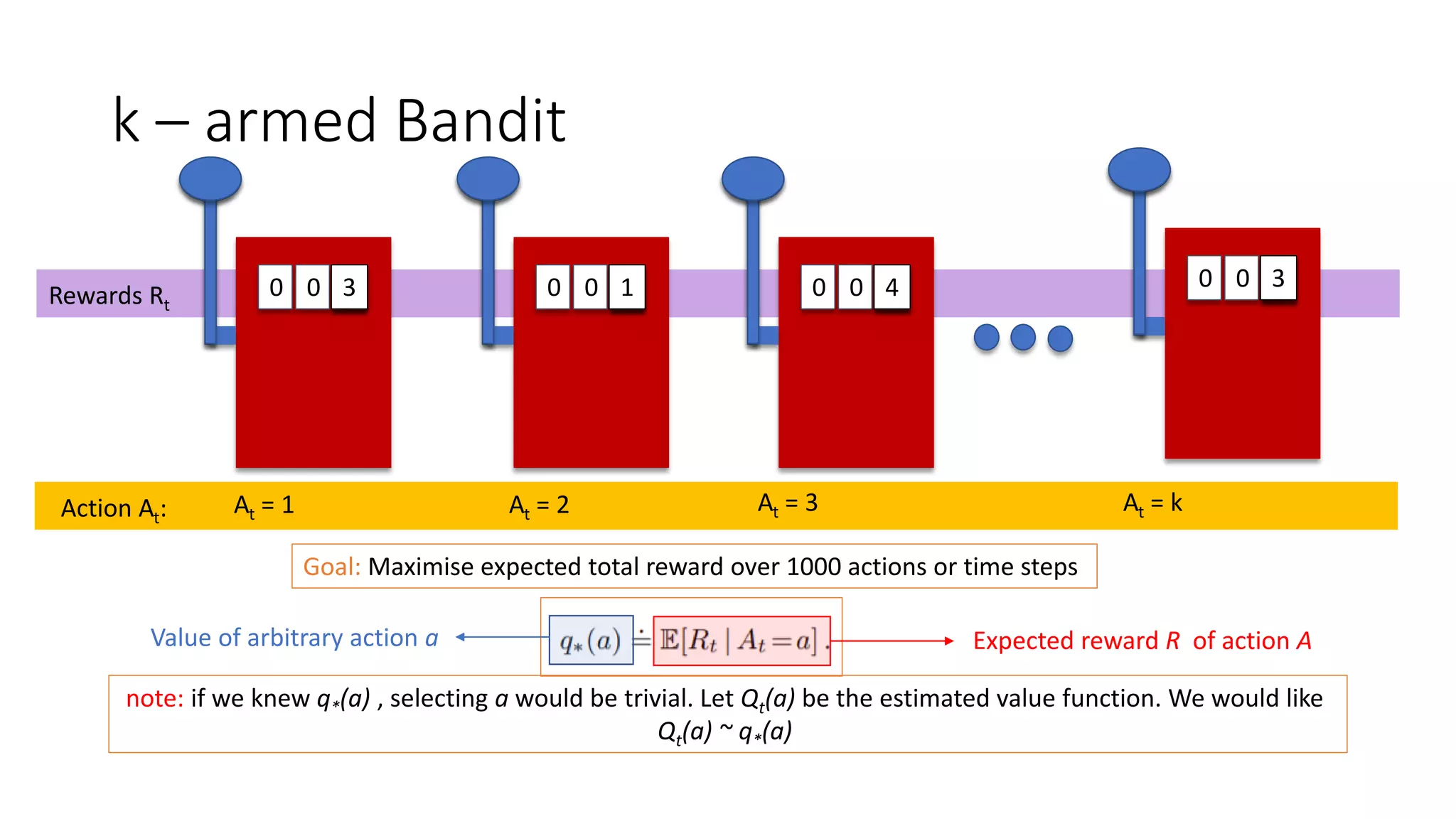
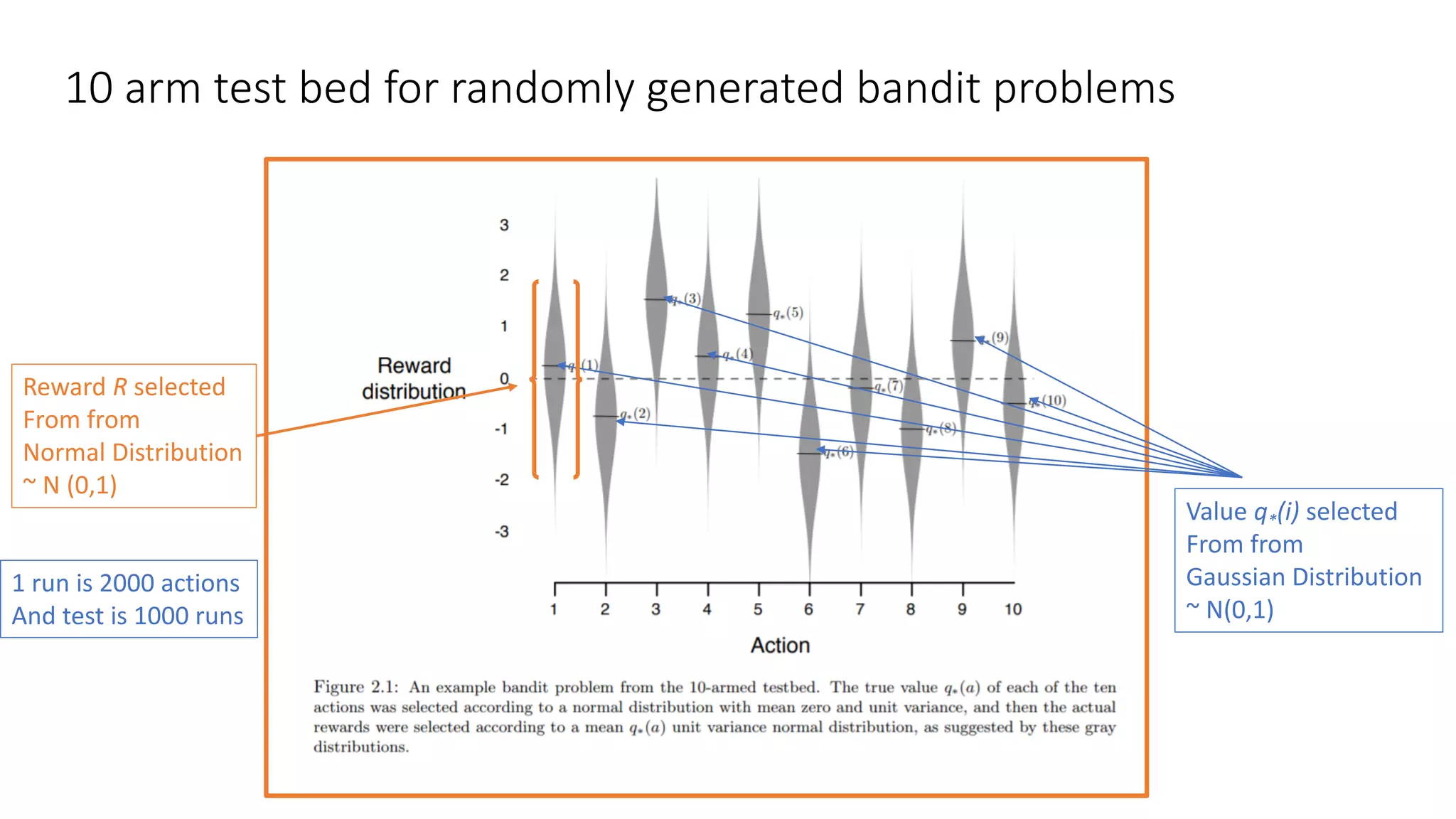
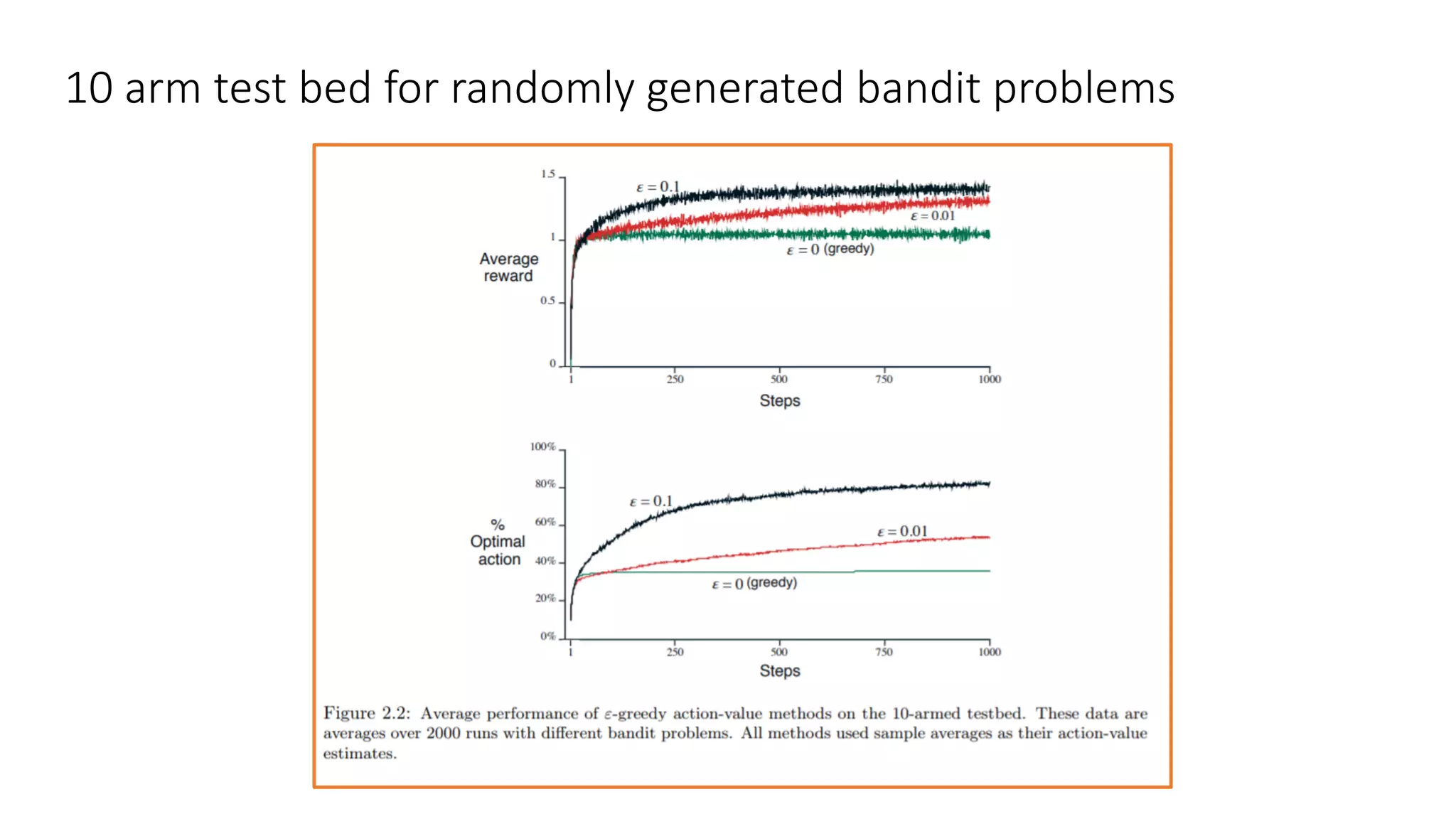
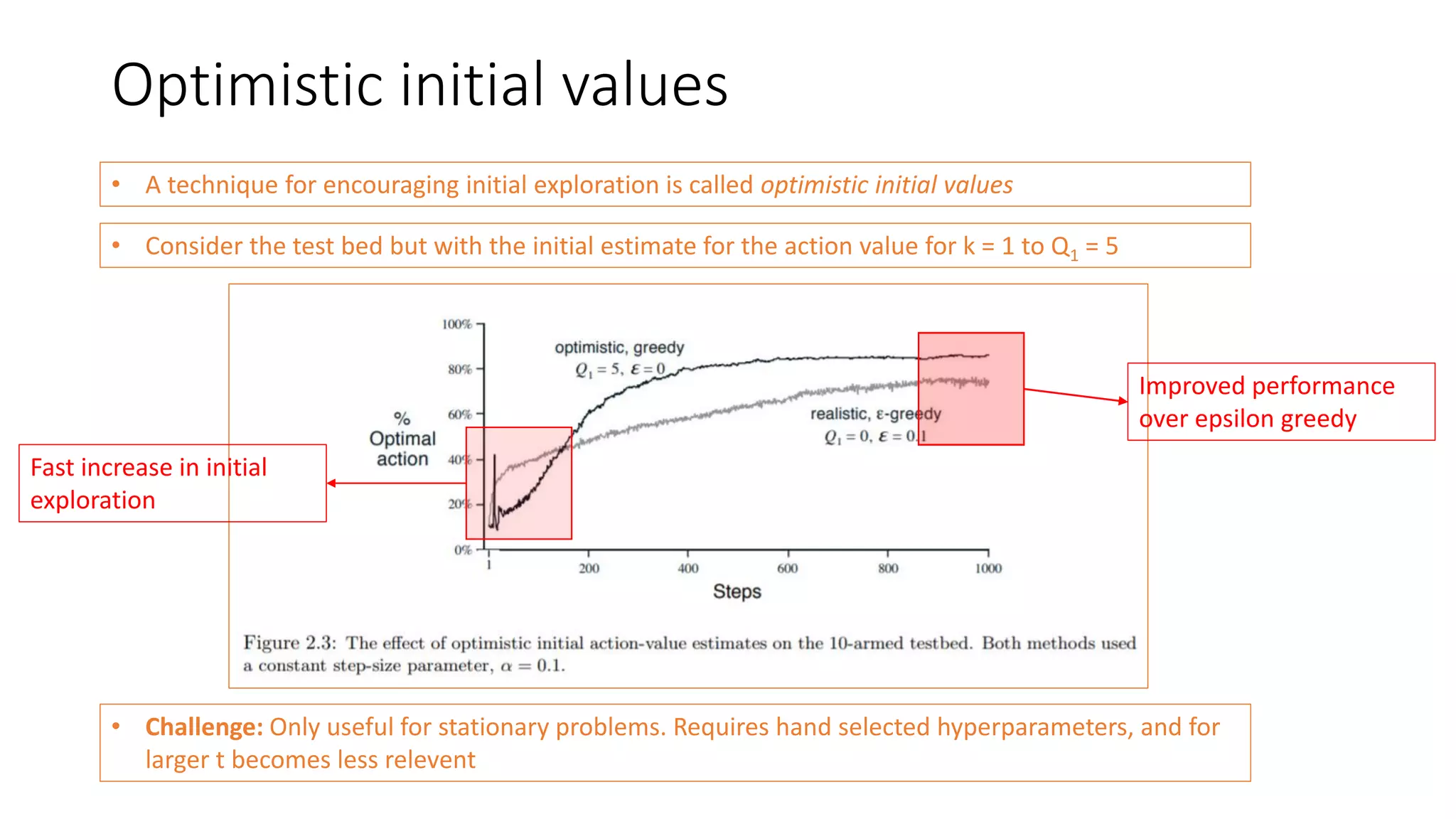
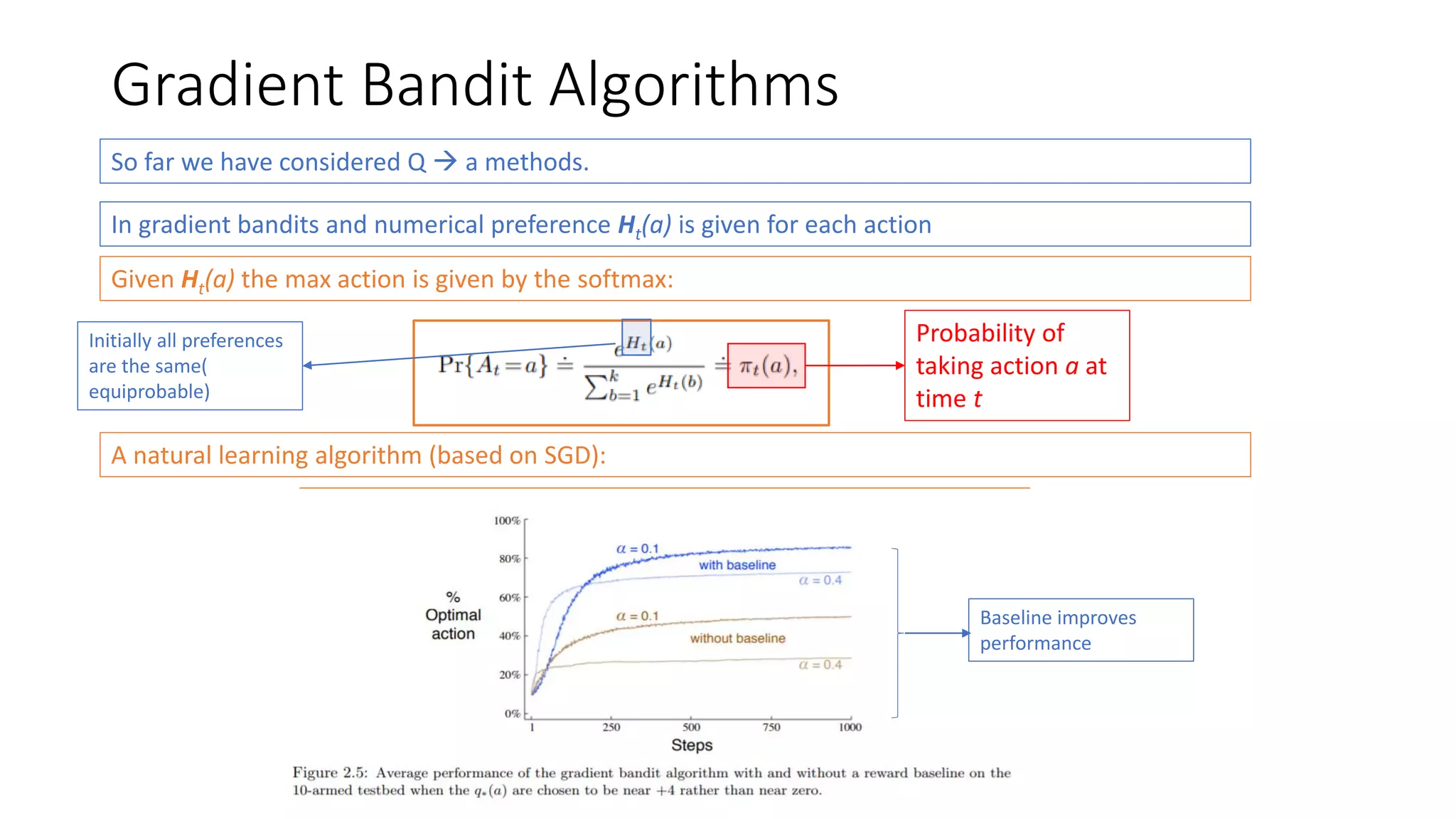
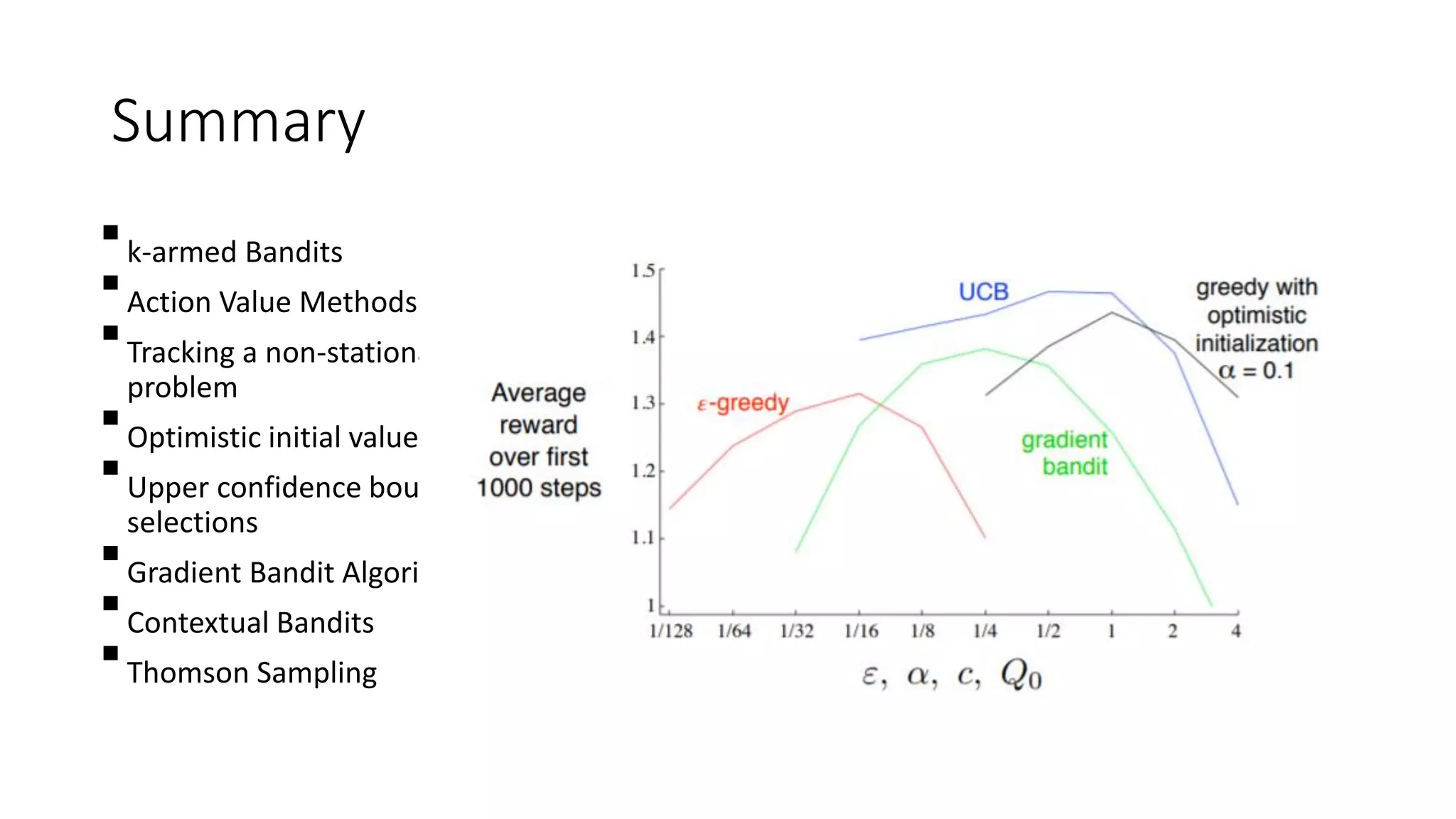
This document discusses various algorithms for multi-armed bandit problems including k-armed bandits, action value methods like epsilon-greedy, tracking non-stationary problems, optimistic initial values, upper confidence bound action selection, gradient bandit algorithms, contextual bandits, and Thomson sampling. The k-armed bandit problem involves choosing actions to maximize reward over time without knowing the expected reward of each action. The document outlines methods for balancing exploration of unknown actions with exploitation of best known actions.

1. Houston Machine Learning
All About Bandits!
4/13/2019
Neilkunal Panchal

2. Outline
• k-armed Bandits
• Action Value Methods
• Tracking a non-stationary problem
• Optimistic initial values
• Upper confidence bound action selections
• Gradient Bandit Algorithms
• Contextual Bandits
• Thomson Sampling

3. Introduction
• Chapter 2 Reinforcement Learning
and introduction (Sutton and Barto
2017)
• http://incompleteideas.net/book/bo
okdraft2017nov5.pdf

4. k – armed Bandit
0 0 0
At = 1 At = 2 At = 3 At = k
Goal: Maximise expected total reward over 1000 actions or time steps
04 0 0 0030 0 0010 0 003
Action At:
Rewards Rt
Value of arbitrary action a Expected reward R of action A
note: if we knew q*(a) , selecting a would be trivial. Let Qt(a) be the estimated value function. We would like
Qt(a) ~ q*(a)

5. k-armed Bandits – Exploration and Exploitation
• Given an estimate of Qt(a) the estimated value function.
• The greedy action is:
a = argmax(Qt(a) )
• When selecting a greedy action. We are exploiting
• When selecting a non- greedy action we are exploring
• Exploring allow us to obtain a better estimate of Qt(a)
• Exploring allows us to obtain better values of a in the long run
• Exploiting is the right thing to do in the short run
Exploration – Exploitation Conflict: Given a single action it not possible to simultaneously explore
and exploit. One must balance short term and long term rewards

6. Action Value Methods epsilon- Greedy
1 if Ai = a
0 otherwise
• Look at methods to better estimate Qt(a)
• Estimate Q by rewards actually received.
Tends to q*(a) as denominator goes to infinity
• Greedy action selection is given by:
Argmax selects the argument which
maximises Q
• Epsilon- Greedy action selection is given by:

7. 10 arm test bed for randomly generated bandit problems
Value q*(i) selected
From from
Gaussian Distribution
~ N(0,1)
Reward R selected
From from
Normal Distribution
~ N (0,1)
1 run is 2000 actions
And test is 1000 runs

8. 10 arm test bed for randomly generated bandit problems

9. Incremental Approach
• How to implement value estimate average Q in a more computationally efficient way?
Estimate of Action Value
After n-1 trials
ith Reward
• The memory requirement grows with n

10. Tracking a non-stationary problem
• The problems we have encountered so far assume a stationary bandit. (Reward probabilities do
not change)
• How do we deal with non-stationary bandits?
• Here we can weight recent rewards more
Constant step size
Exponential recenty weighted average
• General condition for convergence:
Steps are large enough to overcome
initial conditions or random variations
The steps become small enough to
eventually converge
• Condition met for 1/n but not for constant step size. But desired for stationary environments

11. Optimistic initial values
• A technique for encouraging initial exploration is called optimistic initial values
• Consider the test bed but with the initial estimate for the action value for k = 1 to Q1 = 5
Fast increase in initial
exploration
Improved performance
over epsilon greedy
• Challenge: Only useful for stationary problems. Requires hand selected hyperparameters, and for
larger t becomes less relevent

12. Upper confidence bound action selections
Epsilon greedy is a good method for exploration. But doesn’t take into account uncertainty of
estimates. Nor does it explore from near optimal actions.
An improvement is to select actions according to:
Number of times an action is
selected and a measure of
uncertainty
C controls degree of exploration
Improved performance
over epsilon greedy
Works well for bandit
and MCTS isn’t generally
used for RL

13. Gradient Bandit Algorithms
So far we have considered Q  a methods.
In gradient bandits and numerical preference Ht(a) is given for each action
Given Ht(a) the max action is given by the softmax:
Probability of
taking action a at
time t
Initially all preferences
are the same(
equiprobable)
A natural learning algorithm (based on SGD):
Learning rate
Average Reward (Baseline)
Baseline improves
performance

14. Contextual Bandits
0 0 004 0 0 0030 0 0010 0 003
0 0 004 0 0 0030 0 0010 0 003
Rewards Rt
Rewards Rt
Policy
Policy
Policy

15. Thomson Sampling
• https://towardsdatascience.com/solving-multiarmed-bandits-a-comparison-of-epsilon-greedy-and-
thompson-sampling-d97167ca9a50
The Thompson sampler differs quite fundamentally from the e-greedy algorithm in three
major ways:
• it is not greedy;
• its exploration is more sophisticated, and;
• it is Bayesian
• Set a uniform prior distribution between 0 and 1 for each variant k’s payout rate
• Draw parameters theta from each of k’s posterior distribution
• Select the variant k which is the highest parameter theta
• Observe the distribution parameters

16. Summary
k-armed Bandits
Action Value Methods
Tracking a non-stationary
problem
Optimistic initial values
Upper confidence bound action
selections
Gradient Bandit Algorithms
Contextual Bandits
Thomson Sampling