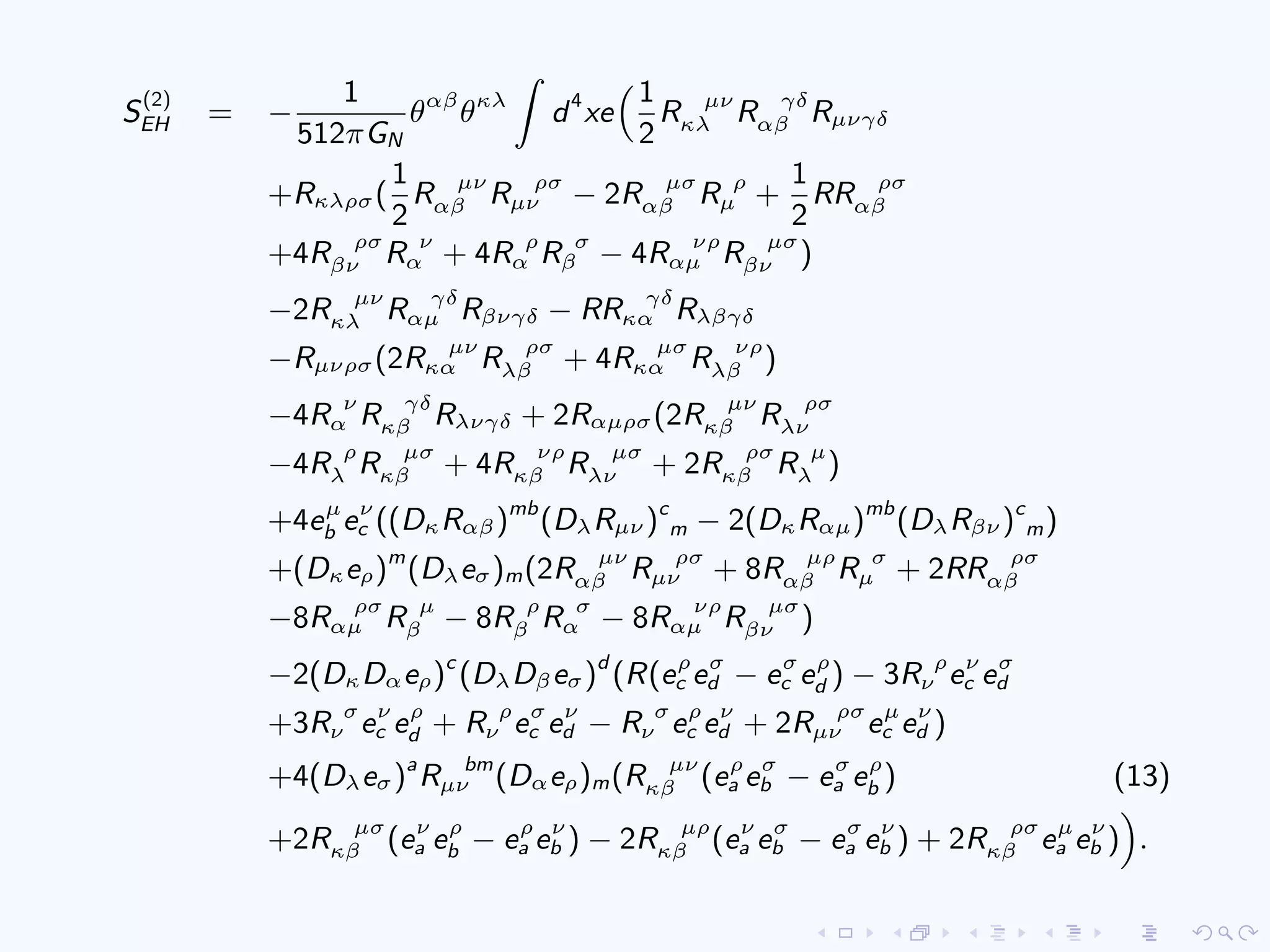- The document describes a talk on noncommutative geometry and gravity theories given at a workshop in Serbia. - Noncommutative geometry arises in string theory and could help address problems in quantum gravity and the standard model. The talk presents an approach using a star product to represent noncommutative algebras. - Actions for noncommutative gauge theory and gravity are discussed. For gravity, a deformation of the MacDowell-Mansouri action is proposed based on the Seiberg-Witten map. This leads to modified field equations and corrections to the Einstein-Hilbert and cosmological constant terms.

1. Balkan Workshop BW2013
-Beyond the Standard Models-,
Vrnjaˇcka Banja, April 25th
-29th
, 2013
Noncommutative gauge and gravity theories
Marija Dimitrijevi´c
University of Belgrade, Faculty of Physics,
Belgrade, Serbia
M. Dimitrijevi´c, V. Radovanovi´c and H. ˇStefanˇci´c, arXiv: 1207.4675[hep-th]
P. Aschieri, L. Castellani and M. Dimitrijevi´c, arXiv: 1207.4346[hep-th]

2. Overview
NC geometry
Motivation
Main results
-product approach
NC gauge theory
NC gravity
Gravity as a gauge theory
AdS inspired NC action
Conclusions & Outlook

3. NC geometry: motivation
Why Noncommutativity? Physics at small distances (high
energies) not very well understood.
Original motivation: to solve the problem of divergences in QFT.
Recent motivation: appears in string theory, playground for
Quantum theory of gravity, new effects in QFT, . . .
[Douglas, Nekrasov ’01; Szabo ’01, ’06,; Castellani ’00;. . . ]
Why deformation of gravity?: No renormalizable gravity theory
(yet), modified gravity theory could explain the problems such as
Dark matter and Dark energy,. . .
Why deformation of gauge theories?: Standard model is not the
final theory, renormalizability, SUSY, cosmological constant
problem, DM particles,. . .
Different approaches: Connes, Wess (Munich group), Grosse,. . .

4. NC geometry: main results
Mathematics: C∗-algebras, deformation quantizaton, Hopf
algebras and quantum groups,. . .
Physics:
-renormalizability of NC field theories: UV/IR mixing,
renormalizable models [Minwalla, Raamsdonk ’99; Grosse, Wulkenhaar ’05;
Buri´c, Radovanovi´c ’04]
-NC Standard Model: predictions of new processes (new vertices)
[Wess et al. ’01; Trampeti´c et al. ’04,’05]. New vertices:
γγγ, γγZ, γZZ, ZZZ, . . .
ff γγ, ff γZ, ffZZ, udγW , . . .

5. -NC SUSY theories: models, renormalization [Seiberg ’03; Britto, Feng,
Rey ’03; Dimitrijevi´c, Radovanovic´c ’09].
-NC gravity: twist approach [Wess et al. ’05, ’06; Ohl, Schenckel ’09],
gauge theory of Lorentz/Poincar´e group [Chamseddine ’01,’04, Cardela,
Zanon ’03, Aschieri, Castellani ’09,’12]: new terms in the action appear
(Rµνρσ)n, . . . .

6. NC geometry: -product approach
Noncommutative space ˆAˆx , generated by ˆxµ coordinates
µ = 0, 1, . . . n such that:
[ˆxµ
, ˆxν
] = Θµν
(ˆx). (1)
It is an associative free algebra generated by ˆxµ and divided by the
ideal generated by relations (1). Differential calculus, integral,
symmetries [Wess et al. ∼1990s] can be discussed, but. . .
-product geometry: represent ˆAˆx on the space of commuting
coordinates, but keep track of the deformation
ˆAˆx → Ax
ˆf (ˆx) → f (x) and ˆf (ˆx)ˆg(ˆx) → f g(x).

7. Example: θ-constant (canonical) deformation leads to Moyal-Weyl
-product:
f g (x) =
∞
n=0
i
2
n 1
n!
θρ1σ1
. . . θρnσn
∂ρ1 . . . ∂ρn f (x) ∂σ1 . . . ∂σn g(x)
= f · g +
i
2
θρσ
(∂ρf ) · (∂σg) + O(θ2
). (2)
Associative, noncommutative; c. conjugation: (f g)∗ = g∗ f ∗.
Derivatives, integral are well defined
d4
x f g = d4
x g f = d4
x fg. (3)
The -product (2) enabled: construction of quantum field theories
and analysis of their renormalizability properties, construction of
NC Standard Model and the analysis of its phenomenological
consequences,. . .

8. NC gauge theory
We work with θ-constant NC space:
f · g → f g = f · g + i
2 θαβ
(∂αf )(∂βg)
−1
8 θαβ
θκλ
(∂α∂κf )(∂β∂λg) + . . .
α, Φ, Aµ, Fµν → ˆα, ˆΦ, ˆAµ,
ˆFµν = ∂µ
ˆAν − ∂ν
ˆAµ − i[ˆAµ , ˆAν]
δαΨ = iαΨ → δα
ˆΨ = i ˆα ˆΨ
δαΦ = i[α, Φ] → δα
ˆΦ = i[ˆα , ˆΦ]
δαAµ = ∂µ + i[α, Aµ] → δα
ˆAµ = ∂µ ˆα + i[ˆα , ˆAµ]
δαFµν = i[α, Fµν] → δα
ˆFµν = i[ˆα , ˆFµν]

9. Idea of the Seiberg-Witten map: NC gauge transformations are
induced by the commutative gauge transformations, δα → δα.
Then
ˆα = ˆα(α, Aµ), ˆAµ = ˆAµ(Aµ), ˆΦ = ˆΦ(Φ, Aµ). (4)
NC gauge transformations have to close
(δαδβ − δβδα)ˆΦ = δ−i[α,β]
ˆΦ.
This conditions enables to solve for ˆα(α, Aµ), [Ulker, Yapiskan ’08,
Aschieri, Castellani ’11]:
ˆα(n+1)
= −
1
4(n + 1)
θκλ
{ˆAκ , ∂λ ˆα}
(n)
, (5)
with
(A B)(n)
= A(n)
B(0)
+ A(n−1)
B(1)
+ . . .
+A(0) (1)
B(n−1)
+ A(1) (1)
B(n−2)
+ . . .

10. The SW-map solution for the NC gauge field ˆAµ follows from
δα
ˆAµ = ∂µ ˆα + i[ˆα , ˆAµ]:
A(n+1)
µ = −
1
4(n + 1)
θκλ
{ˆAκ , ∂λ
ˆAµ + ˆFλµ}
(n)
, (6)
with the NC field-strength tensor ˆFλµ.
Similarly, one calculates solutions of the SW-map for matter fields,
field-strength tensor,. . .
NC U(1) action, expanded up to first order in the NC parameter
θαβ
S = −
1
4
d4
x ˆFµν
ˆFµν
= d4
x −
1
4
FµνFµν
+ θαβ
(
1
4
FαβFµνFµν
− FαµFβνFµν
) .(7)
The commutative abelian gauge theory becomes a NC nonabelian
gauge theory ⇒ Photon self-interactions appear!

11. The main result of the SW-map: No new degrees of freedom, NC
gauge theory and the corresponding commutative gauge theory
have the same number of degrees of freedom! This enables
construstion and analysis of NC gauge theories.
NC Standard Model [Wess et al. ’01,’02]:
-phenomenology: [Trampeti´c et al. ’03,’05, . . . ],
-renormalization: [Buri´c, Radovanovi´c ’03,. . . , 11; Martin, Tamarit ’05,’07,. . . ]

12. NC gravity: gravity as a gauge theory
Localization of space-time symmetry ⇒ gravity.
Start from the MacDowell-Mansouri action [MacDowell, Mansouri ’77]:
S =
1
16πGN
d4
x
l2
16
µνρσ
abcd R ab
µν R cd
ρσ +
√
−gR − 2
√
−gΛ (8)
and Λ = −3/l2,
√
−g = det e a
µ . Comments:
-variables in (8) are spin connection ωµ and vielbeins eµ. They are
independent, 1st order formalsim.
-(8) is invariant under SO(1, 3) gauge symmetry, while the
diffeomorphism symmetry appears as a consequence of SSB, see
[Stelle, West ’80].
-varying (8) with respect to ωµ and vielbeins eµ gives equations of
motion for these fields.
-(8) written in the 2nd order formalism has three terms:
Gauss-Bonnet topological term, Einstein-Hilbert term and the
cosmological constant term.

13. NC gravity: AdS inspired NC action
The NC generalization of the action (8) is
S = −
il2
64πGN
d4
x µνρσ
Tr (ˆRµν
ˆRρσγ5) (9)
−
2i
l2
Tr (ˆRµν
ˆEρ
ˆEσγ5) +
1
l4
Tr (ˆEµ
ˆEν
ˆEρ
ˆEσγ5) ,
with:
-NC SO(1, 3) gauge potential: ˆωµ = ωµ + ˆω
(1)
µ + ˆω
(2)
µ + . . .
-NC vielbeins: ˆEµ = eµ + ˆE
(1)
µ + ˆE
(2)
µ + . . .
-NC curvature tensor:
ˆRµν = ∂µ ˆων − ∂ν ˆωµ − i[ˆωµ , ˆων]
= Rµν + ˆR(1)
µν + ˆR(2)
µν + . . . .

14. Solutions of the SW map we insert into the action (9) and
calculate corrections. We find:
S(0)
= commutative action (8)
S(1)
= 0 unfortunately!!!
S(2)
= very complicated, not manifestly gauge invariant,
no explicit results existed until June 2012.
Shortcut: SW map for composite fields [Aschieri, Castellani, Dimitrijevi´c,
’12].
An example:
(ˆEµ
ˆEν)(1)
= ˆE(1)
µ eν + eµ
ˆE(1)
ν +
i
2
θαβ
∂αeµ∂βeν (10)
= −
1
4
θαβ
{ωα, ∂β(eµeν) + Dβ(eµeν)} +
i
2
θαβ
(Dαeµ)(Dβeν).

15. Inserting these expressions and calculating traces explicitly, we
obtain
S
(2)
GB = −
l2
1024πGN
θκλ
θρσ µναβ
abcd d4
x R cd
αβ R ab
µκ R mn
νρ Rλσmn
−
1
2
R cd
αβ R ab
µκ R mn
νλ Rρσmn + R mn
αβ RµκmnR ab
νρ R cd
λσ
+R mn
µρ RνσmnR ab
ακ R cd
βλ −
1
2
R ab
ακ R cd
βλ R mn
ρσ Rµνmn , (11)
S
(2)
CC = −
1
512πGN l2
θκλ
θαβ
d4
xe 6R ab
κα Rλβab − 3R ab
αβ Rκλab
+4R γδ
αβ (Dκeµ)a
(Dλeγ)b
(eµ
a eδb + eµ
b eδa) (12)
−4R γδ
αβ (Dκeγ)a
(Dλeδ)a + 4(DκDαeµ)a
(DλDβeν )b
(eµ
a eν
b − eµ
b eν
a )
−8R γδ
κα (Dβeγ)a
(Dλeδ)a + 8R γδ
κα (Dβeγ)a
(Dλeµ)b
(eµ
a eδb + eµ
b eδa) ,

16. S
(2)
EH = −
1
512πGN
θαβ
θκλ
d4
xe
1
2
R µν
κλ R γδ
αβ Rµνγδ
+Rκλρσ(
1
2
R µν
αβ R ρσ
µν − 2R µσ
αβ R ρ
µ +
1
2
RR ρσ
αβ
+4R ρσ
βν R ν
α + 4R ρ
α R σ
β − 4R νρ
αµ R µσ
βν )
−2R µν
κλ R γδ
αµ Rβνγδ − RR γδ
κα Rλβγδ
−Rµνρσ(2R µν
κα R ρσ
λβ + 4R µσ
κα R νρ
λβ )
−4R ν
α R γδ
κβ Rλνγδ + 2Rαµρσ(2R µν
κβ R ρσ
λν
−4R ρ
λ R µσ
κβ + 4R νρ
κβ R µσ
λν + 2R ρσ
κβ R µ
λ )
+4eµ
b eν
c ((DκRαβ)mb
(DλRµν )c
m − 2(DκRαµ)mb
(DλRβν )c
m)
+(Dκeρ)m
(Dλeσ)m(2R µν
αβ R ρσ
µν + 8R µρ
αβ R σ
µ + 2RR ρσ
αβ
−8R ρσ
αµ R µ
β − 8R ρ
β R σ
α − 8R νρ
αµ R µσ
βν )
−2(DκDαeρ)c
(DλDβeσ)d
(R(eρ
c eσ
d − eσ
c eρ
d ) − 3R ρ
ν eν
c eσ
d
+3R σ
ν eν
c eρ
d + R ρ
ν eσ
c eν
d − R σ
ν eρ
c eν
d + 2R ρσ
µν eµ
c eν
d )
+4(Dλeσ)a
R bm
µν (Dαeρ)m(R µν
κβ (eρ
a eσ
b − eσ
a eρ
b ) (13)
+2R µσ
κβ (eν
a eρ
b − eρ
a eν
b ) − 2R µρ
κβ (eν
a eσ
b − eσ
a eν
b ) + 2R ρσ
κβ eµ
a eν
b ) .

17. Conclusions & Outlook
NC gauge theory
-NCSM: no new fields, but new interactions appear;
renormalizability and phenomenology studied,. . .
-NC gravity: MacDowell-Mansouri action studied, expansion
up to second order in the NC parameter written in a
manifestly gauge covariant way; phenomenological
consequences remain to be studied,. . .
future investigation
-phenomenological consequences of NC gravity
-NC SO(2, 3) symmetry and SSB in NC theory
-SW map for composite fields and renormalization of gauge
theories