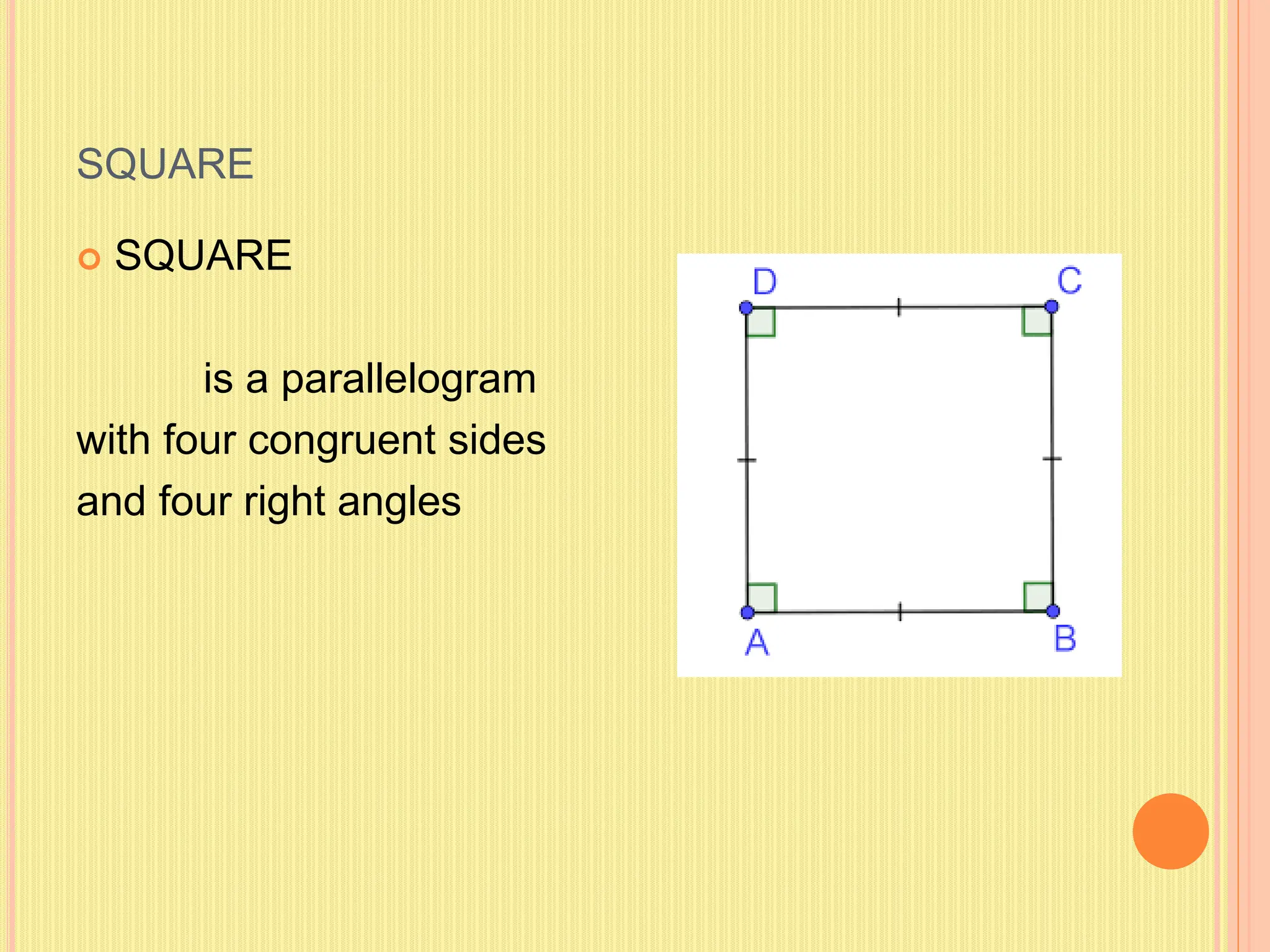
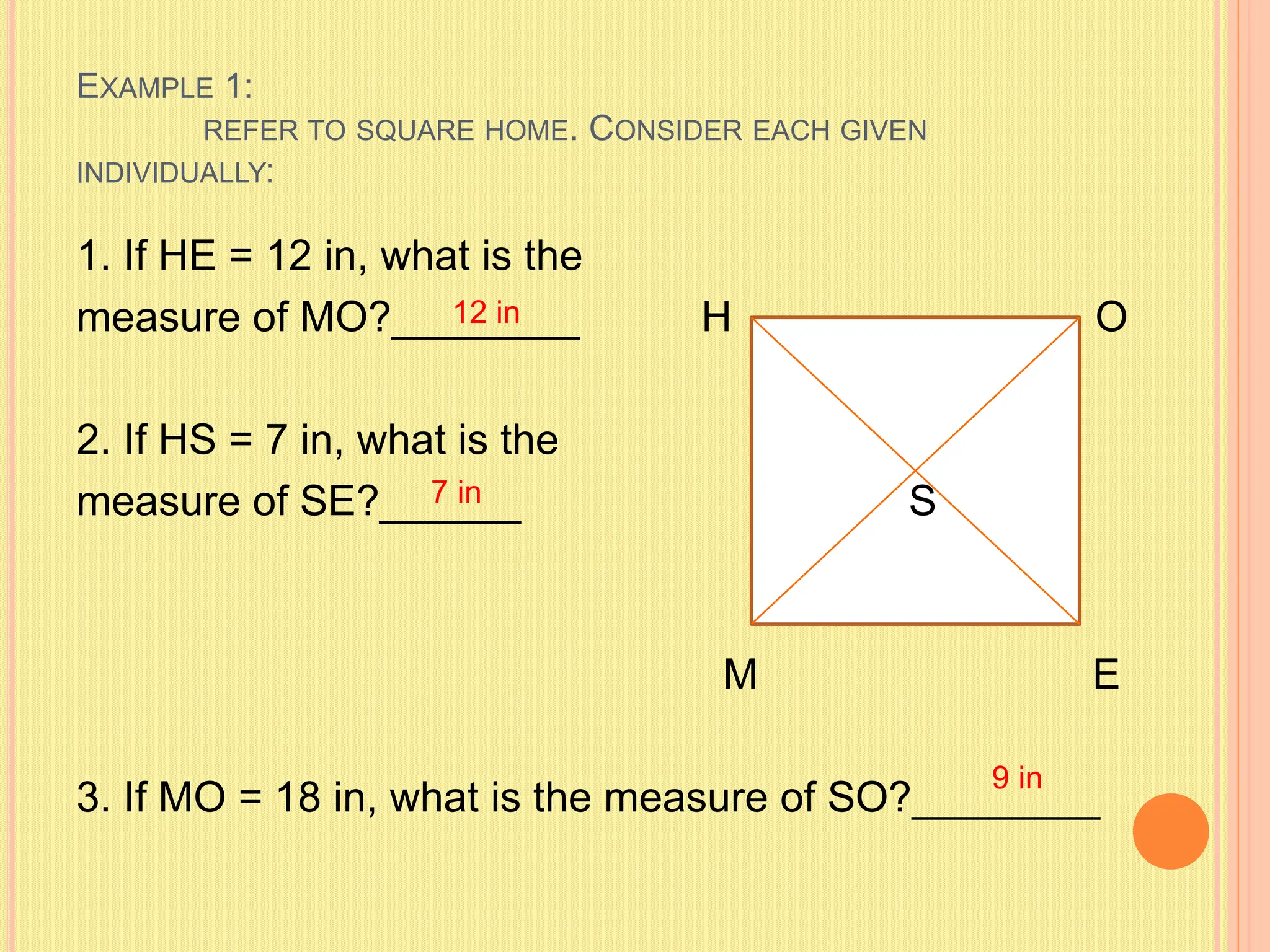
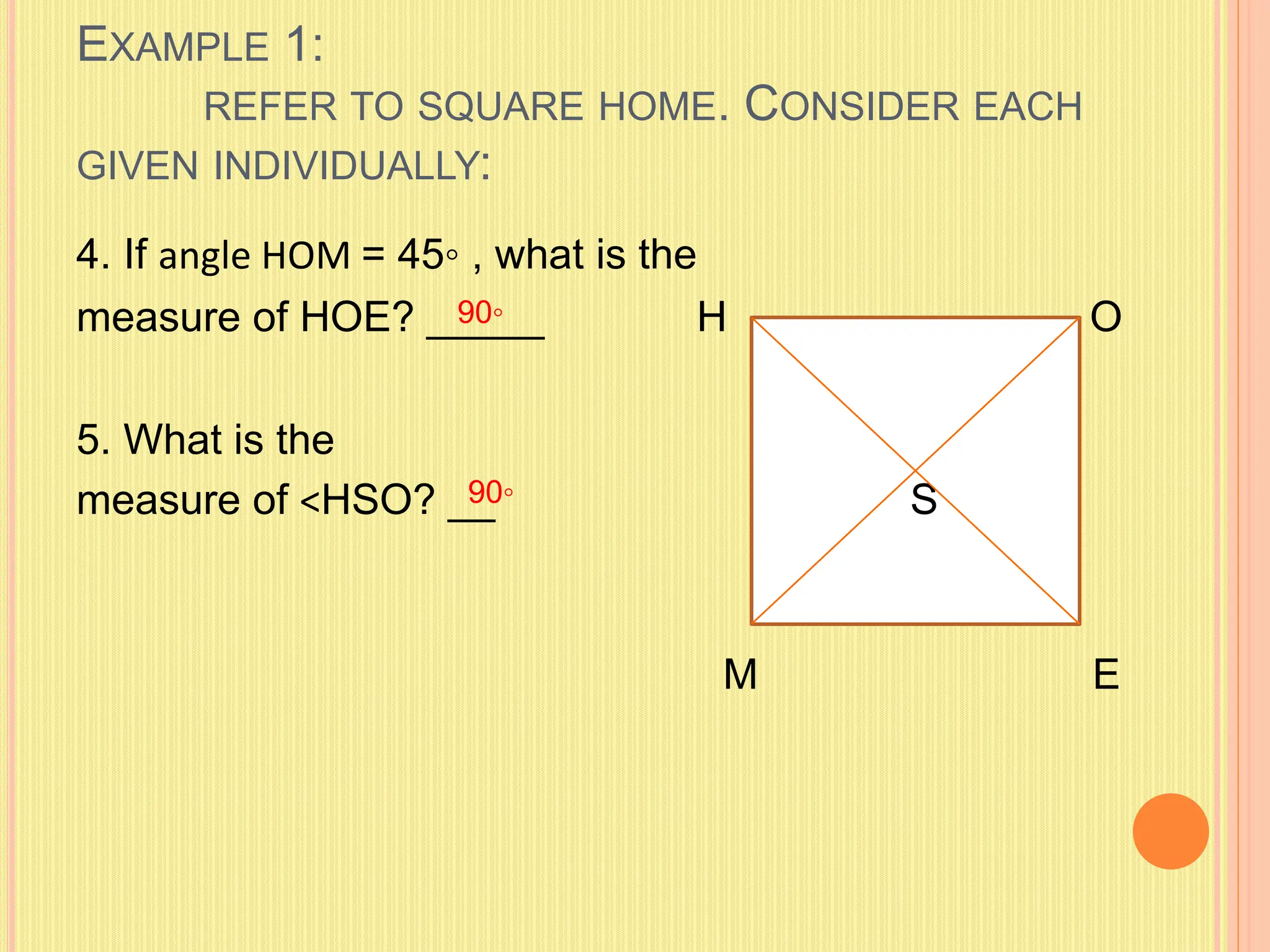
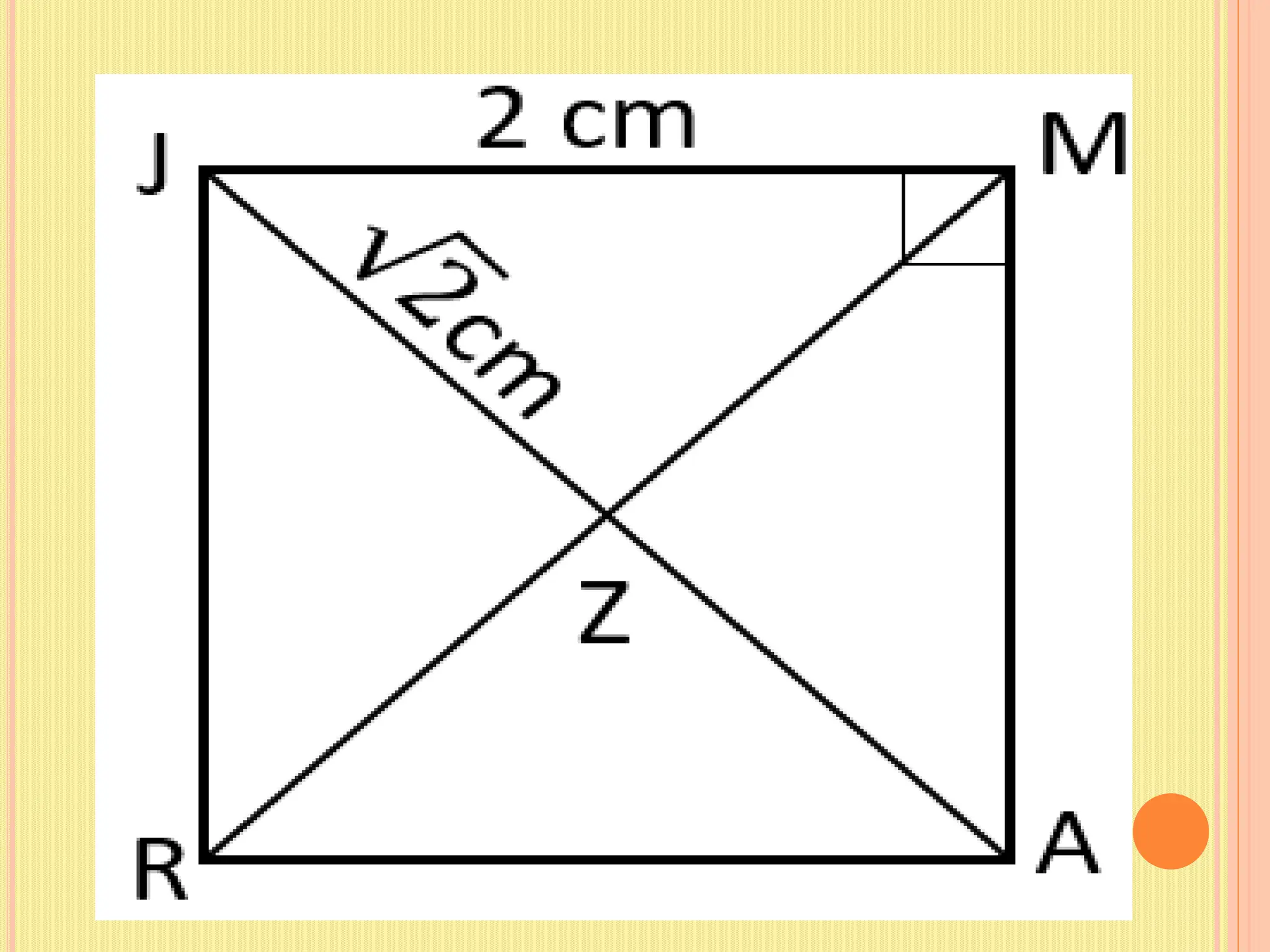
This document discusses theorems related to squares. It defines a square as a parallelogram with four congruent sides and four right angles. It presents four theorems: 1) if a parallelogram has a right angle, it is a rectangle; 2) the diagonals of a rectangle are congruent; 3) the diagonals of a rhombus are perpendicular; 4) each diagonal of a rhombus bisects the other. It applies these theorems to squares, provides examples of solving problems involving squares, and gives properties and assessment questions about squares.

2. MATH 9
THEOREMS RELATED TO SQUARE

3. LEARNING TARGETS:
 Define square
 Apply the theorems on square in solving problems

4. SQUARE
 SQUARE
is a parallelogram
with four congruent sides
and four right angles

5. THE SQUARE IS THE MOST ESPECIAL PARALLELOGRAM BECAUSE ALL THE
PROPERTIES OF PARALLELOGRAM AND THE THEOREMS ON RECTANGLE AND
RHOMBUSES ARE TRUE TO ALL SQUARE
Theorem 1: If a parallelogram
has a right angle, then is has
four right angles and the
parallelogram is a rectangle.
Theorem 2: The diagonals of a
rectangle are congruent.
Theorem 3: The diagonals of a
rhombus are perpendicular.
Theorem 4: Each diagonal of a
rhombus bisect each other.
THEOREMS ON RECTANGLES
THEOREMS ON RHOMBUS

6. THE SQUARE IS THE MOST ESPECIAL PARALLELOGRAM BECAUSE ALL THE
PROPERTIES OF PARALLELOGRAM AND THE THEOREMS ON RECTANGLE AND
RHOMBUSES ARE TRUE TO ALL SQUARE
Theorem 1: If a parallelogram
has a right angle, then is has
four right angles and the
parallelogram is a SQUARE.
Theorem 2: The diagonals of a
SQUARE are congruent.
Theorem 3: The diagonals of a
SQUARE are perpendicular.
Theorem 4: Each diagonal of a
SQUARE bisect each other.
THEOREMS ON SQUARE
THEOREMS ON SQUARE

7. EXAMPLE 1:
REFER TO SQUARE HOME. CONSIDER EACH GIVEN
INDIVIDUALLY:
1. If HE = 12 in, what is the
measure of MO?________ H O
2. If HS = 7 in, what is the
measure of SE?______ S
M E
3. If MO = 18 in, what is the measure of SO?________
12 in
7 in
9 in

8. EXAMPLE 1:
REFER TO SQUARE HOME. CONSIDER EACH
GIVEN INDIVIDUALLY:
4. If angle HOM = 45◦ , what is the
measure of HOE? _____ H O
5. What is the
measure of <HSO? __ S
M E
90◦
90◦

9. ACTIVITY 1
 DETERMINE WHETHER THE STATEMENT IS NEVER
TRUE, SOMETIMES TRUE, OR ALWAYS TRUE

10. ALL SQUARE ARE PARALLELOGRAM
ALWAYS TRUE
 A SQUARE IS A PARALLELOGRAM

11. A RECTANGLE IS A SQUARE
 SOMETIMES TRUE
A rectangle is a parallelogram with four
right angles. It is possible to draw a
rectangle with four congruent sides.

12. A SQUARE IS A RECTANGLE
 ALWAYS TRUE
 THEOREM NO. 1 on rectangle, A square is a
parallelogram with four right angles, hence it is rectanlge.

13. ALL RHOMBUSES ARE SQUARE
 NEVER TRUE

14. A SQUARE IS A RHOMBUS
 ALWAYS TRUE
 Because all its sides are congruent, It matches the
definition of rhombus

15. A SQUARE IS A VERY SPECIAL TYPE OF
PARALLELOGRAM
 BECAUSE IT HAS THE PROPERTIES OF A
PARALLELOGRAM, A RECTANGLE AND A
RHOMBUS

16. PROPERTIES OF SQUARE
 All four sides are
 All four angles are
 Opposite sides are
 Two consecutive angles are
 Diagonals each other
 Diagonals are and
 Each diagonal opposite angle
 Each diagonal divides the square into two
triangle.

17. ASSESSMENT
Using the diagram of square
JMAR with its diagonals
intersecting at Z, and given that
JA= 2 cm and JZ = √ 2 cm, find the
measures of the following quantities