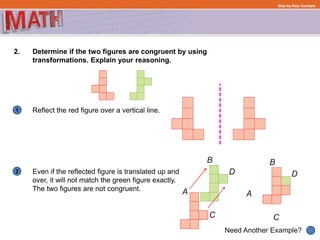
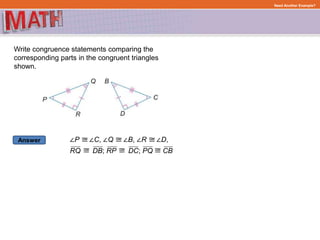
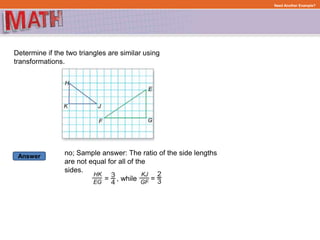
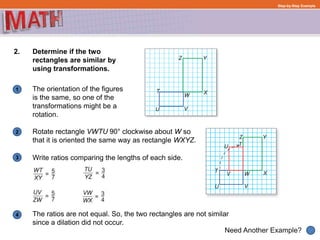
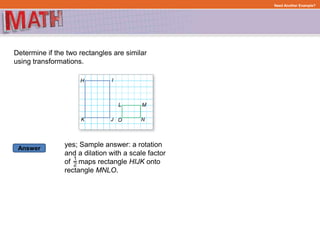
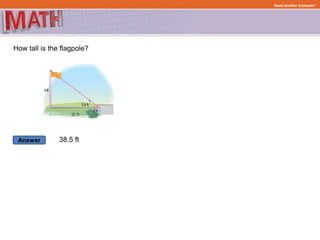
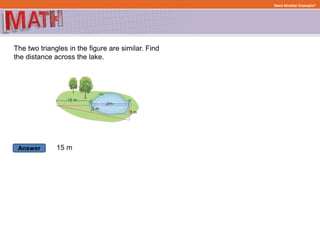
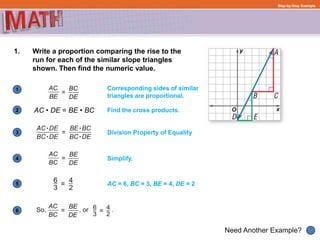
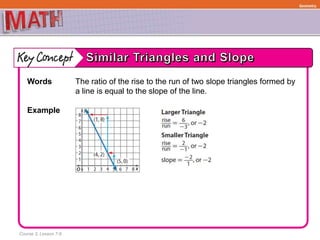
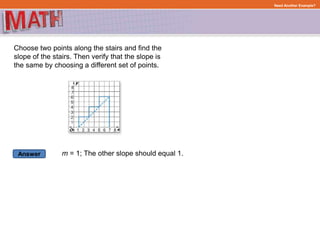
The document provides examples and step-by-step explanations for solving geometry problems involving similar and congruent shapes using transformations and properties of similarity and congruence. In one example, it is determined that two triangles are similar because corresponding angles are congruent. In another example, transformations of a rotation and translation are used to show that two figures are congruent.

1. Answer
Need Another Example?
Determine if the two figures are congruent by
using transformations. Explain your reasoning.
congruent; A rotation followed by a
translation maps figure A onto figure B.

2. 1
Need Another Example?
2
Step-by-Step Example
2. Determine if the two figures are congruent by using
transformations. Explain your reasoning.
Reflect the red figure over a vertical line.
Even if the reflected figure is translated up and
over, it will not match the green figure exactly.
The two figures are not congruent.

3. Answer
Need Another Example?
Determine if the two figures are congruent by
using transformations. Explain your reasoning.
Not congruent; no transformations will
match the figures up exactly.

4. 1
Need Another Example?
2
3
Step-by-Step Example
3. Ms. Martinez created the logo shown. What transformations did she
use if the letter “d” is the preimage and the letter “p” is the image?
Are the two figures congruent?
Start with the preimage. Rotate the letter “d”
180° about point A.
Translate the new image up.
A
A
Ms. Martinez used a rotation and translation to
create the logo. The letters are congruent
because images produced by a rotation and
translation have the same shape and size.

5. Answer
Need Another Example?
The pattern below appears along the edge of a
plate. What transformations could be used if the
first figure is the preimage and the second is the
image?
Sample answer: a rotation followed by a
translation

6. • corresponding parts
Symbols
• is congruent to
Course 3, Lesson 7-2

Geometry

7. Course 3, Lesson 7-2
Geometry
Words If two figures are congruent, their corresponding sides are
congruent and their corresponding angles are congruent.
Model
Symbols
Congruent Angles:
Congruent Sides:
ABC DEF
; ;A D B E C F     
; ;AB DE BC EF CA FD  

8. 1
Need Another Example?
2
3
Step-by-Step Example
1. Write congruence statements
comparing the corresponding parts
in the congruent triangles shown.
Use the matching arcs and tick marks to identify
the corresponding parts.
Corresponding angles: ∠J ∠G, ∠L ∠I, ∠K ∠H
Corresponding sides: JK GH, KL HI, LJ IG

9. Answer
Need Another Example?
Write congruence statements comparing the
corresponding parts in the congruent triangles
shown.
∠P ∠C, ∠Q ∠B, ∠R ∠D,
RQ DB; RP DC; PQ CB

10. Determine any changes in the orientation of the triangles. The orientation is
reversed so at least one of the transformations is a reflection. If you reflect
ABC over the y-axis and then translate it down 2 units it coincides with XYZ.
1
Need Another Example?
2
3
Step-by-Step Example
2. Triangle ABC is
congruent to XYZ.
Write congruence
statements comparing
the corresponding
parts. Then determine
which transformations
map ABC onto XYZ.
The transformations that map ABC onto XYZ consist of a
reflection over the y-axis followed by a translation of 2 units down.
Analyze the figures to determine which angles and sides of the figures correspond.
Corresponding angles: ∠A ∠X, ∠B ∠Y, ∠C ∠Z
Corresponding sides: AB XY, BC YZ, CA ZX

11. Answer
Need Another Example?
Triangle RST is congruent to NML. Write
congruence statements comparing the
corresponding parts. Then determine which
transformation(s) maps RST onto NML.
∠R ∠N, ∠S ∠M, ∠T ∠L,
RS NM; RT NL; ST ML;
Sample answer: If you reflect RST over
the x-axis and then translate it to the left
6 units, it coincides with NML.

12. 1
Need Another Example?
Step-by-Step Example
3. Miley is using a brace to support a tabletop. In the figure, BCE DFG.
If m∠CEB = 50°, what is the measure of ∠FGD?
Since ∠CEB and ∠FGD are corresponding parts in congruent
figures, they are congruent. So, ∠FGD measures 50°.

13. Answer
Need Another Example?
In the figure below, quadrilateral ABCD is congruent to
quadrilateral WXYZ. What is the measure of ∠X?
145°

14. • similar
Course 3, Lesson 7-3
Geometry

15. Translate DEF down 2 units and 5 units to the right so
D maps onto G.
1
Need Another Example?
2
3
Step-by-Step Example
1. Determine if the two
triangles are similar by
using transformations.
Since the orientation of the figures is the same, one of the
transformations is a translation.
Write ratios comparing the lengths of each side.
4 Since the ratios are equal, HGI is the dilated image of EDF. So,
the two triangles are similar because a translation and a dilation maps
EDF onto HGI.

16. Answer
Need Another Example?
Determine if the two triangles are similar using
transformations.
no; Sample answer: The ratio of the side lengths
are not equal for all of the
sides.
= , while =

17. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. Determine if the two
rectangles are similar by
using transformations.
The orientation of the figures
is the same, so one of the
transformations might be a
rotation.
Rotate rectangle VWTU 90° clockwise about W so
that it is oriented the same way as rectangle WXYZ.
Write ratios comparing the lengths of each side.
The ratios are not equal. So, the two rectangles are not similar
since a dilation did not occur.

18. Answer
Need Another Example?
Determine if the two rectangles are similar
using transformations.
yes; Sample answer: a rotation
and a dilation with a scale factor
of maps rectangle HIJK onto
rectangle MNLO.

19. 1
Need Another Example?
2
3
Step-by-Step Example
3. Ken enlarges a photo by a scale factor of 2 for his webpage. He then
enlarges the webpage photo by a scale factor of 1.5 to print. If the
original photo is 2 inches by 3 inches, what are the dimensions of the
print? Are the enlarged photos similar to the original?
Multiply each dimension of the original photo by 2 to find the
dimensions of the webpage photo.
So, the webpage photo will be 4 inches by 6 inches. Multiply the
dimensions of that photo by 1.5 to find the dimensions of the print.
The printed photo will be 6 inches by 9 inches. All three photos
are similar since each enlargement was the result of a dilation.
2 in. × 2 = 4 in. 3 in. × 2 = 6 in.
4 in. × 1.5 = 6 in. 6 in. × 1.5 = 9 in.

20. Answer
Need Another Example?
A baker is reducing an 8-inch by 10-inch photo to place
the image on a cake. He reduces it by a scale factor of
0.8. Then decides the image is still too large, and
reduces it by a scale factor of 0.9. What are
the dimensions of the final image? Is the reduced
image similar to the original?
5.76 in. × 7.2 in.; yes

21. • similar polygons
• scale factor
Symbols
• is similar to
Course 3, Lesson 7-4
Geometry

22. Course 3, Lesson 7-4
Geometry
Words If two polygons are similar, then
• their corresponding angles are congruent and
• the measures of their corresponding sides are proportional.
Model
Symbols , , ,
AB BC AC
A X B Y C Z
XY YZ XZ
          and

23. 1
Need Another Example?
2
3
Step-by-Step Example
1. Determine whether
rectangle HJKL is
similar to rectangle
MNPQ. Explain.
First, check to see if corresponding
angles are congruent.
Since the two polygons are rectangles, all of their angles are right
angles. Therefore, all corresponding angles are congruent.
Next, check to see if corresponding sides are proportional.
Since and are not equivalent, the rectangles are not similar.

24. Answer
Need Another Example?
Determine whether triangle DEF is similar to
triangle HJK. Explain.
Yes; the corresponding angles are
congruent and

25. 1
Need Another Example?
2 3
Step-by-Step Example
2. Quadrilateral WXYZ is similar to quadrilateral ABCD.
a.
Find the scale factor from quadrilateral
ABCD to quadrilateral WXYZ.
So, a length on polygon WXYZ is times
as long as the corresponding length on
polygon ABCD. Let m represent the
measure of XY.
Set up a proportion to find the
missing measure.
a. Describe the transformations that map
WXYZ onto ABCD.
b. Find the missing measure.
Since the figures are similar, they are not the same size. Choose two
corresponding sides and determine what transformations will map one
onto the other. A translation followed by a dilation will map AB onto WX.
b.
scale factor: = or
m = (12) Write the equation.
Multiply.
Write the proportion.
XY = m, BC = 12, YZ = 15,
CD = 10
Find the cross products.
Simplify.
Division Property of Equality
m • 10 = 12 • 15
10m = 180
m = 18
m = 18

26. Answer
Need Another Example?
Rectangle LMNO is similar to rectangle GHIJ.
a. Describe the transformations that map GHIJ onto LMNO.
b. Find the missing measure.
a. Since the figures are similar, they are
not the same size. The transformation
is a translation and a dilation.
b. 6

27. • indirect measurement
Course 3, Lesson 7-5
Geometry

28. Course 3, Lesson 7-5
Geometry
Words If two angles of one triangle are congruent to two angles of
another triangle, then the triangles are similar.
Symbols If
Model
, , .A F B G ABC FGH     and then

29. 1
Need Another Example?
Step-by-Step Example
1. Determine whether the triangles are similar. If so, write a
similarity statement.
Angle A and ∠E have the same measure, so they are congruent. Since
180 – 62 – 48 = 70, ∠G measures 70°. Two angles of EFG are
congruent to two angles of ABC, so ABC ~ EFG.

30. Answer
Need Another Example?
Determine whether the triangles are similar. If
so, write a similarity statement.
The triangles are not similar.

31. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. A fire hydrant 2.5 feet
high casts a 5-foot
shadow. How tall is a
street light that casts a
26-foot shadow at the
same time? Let h
represent the height of
the street light.
Shadow Height
hydrant hydrant
street light street light
=
5 2.5
h26
5h = 26 • 2.5
5h = 65
Find the cross products.
Multiply.
Divide each side by 5.
The street light is 13 feet tall.
h = 13

32. Answer
Need Another Example?
How tall is the flagpole?
38.5 ft

33. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
3. In the figure at the
right, triangle DBA is
similar to triangle
ECA. Ramon wants
to know the distance
across the lake.
320d = 482 • 40
d = 60.25
AB corresponds to AC and BD corresponds to CE.
Find the cross products.
The distance across the lake is 60.25 meters.
Replace AB with 320, AC with 482, and BD with 40.
Multiply. Then divide each side by 320.

34. Answer
Need Another Example?
The two triangles in the figure are similar. Find
the distance across the lake.
15 m

35. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
1. Write a proportion comparing the rise to the
run for each of the similar slope triangles
shown. Then find the numeric value.
AC • DE = BE • BC
Corresponding sides of similar
triangles are proportional.
Find the cross products.
Division Property of Equality
Simplify.
AC = 6, BC = 3, BE = 4, DE = 2

36. Answer
Need Another Example?
Graph ABC with vertices A(−4, 2), B(−4, −2), and
C(−2, −2), and CDF with vertices C(−2, −2),
D(−2, −4), and F(−1, −4). Then write a proportion
comparing the rise to the run for each of the similar
slope triangles and find the numeric value.
;

37. Course 3, Lesson 7-6
Geometry
Words The ratio of the rise to the run of two slope triangles formed by
a line is equal to the slope of the line.
Example

38. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
2. The pitch of a roof refers to the slope of
the roof line. Choose two points on the
roof and find the pitch of the roof shown.
Then verify that the pitch is the same by
choosing a different set of points.
The pitch of the roof is . Verify that the pitch is the same using
two other points.
Formula for slope
Use the points S and R.
(x1, y1) = (8, 6) and (x2, y2) = (12, 8)
Formula for slope
Simplify.
Use the points U and T.
(x1, y1) = (2, 3) and (x2, y2) = (0, 2)
7 Simplify. The pitch is the same.

39. Answer
Need Another Example?
Choose two points along the stairs and find the
slope of the stairs. Then verify that the slope is
the same by choosing a different set of points.
m = 1; The other slope should equal 1.

40. Course 3, Lesson 7-7
Geometry
Perimeter
Words If figure B is similar to figure A by a scale
factor, then the perimeter of B is equal to
the perimeter of A times the scale factor.
Symbols perimeter of perimeter of
figure B figure A
Models
Area
Words If figure B is similar to figure A by a scale
factor, then the area of B is equal to the
area of A times the square of the scale
factor.
Symbols area of area of
figure B figure A
= • scale factor
= • (scale factor)2

41. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
1. Two rectangles are similar. One has a length of 6 inches and
a perimeter of 24 inches. The other has a length of 7 inches.
What is the perimeter of this rectangle?
The scale factor is . The perimeter of the original is 24 inches.
Multiply by the scale factor.
Simplify.
Divide out common factors.
4
1
x = 28
So, the perimeter of the new rectangle is 28 inches.

42. Answer
Need Another Example?
Two rectangles are similar. One has a length
of 10 inches and a perimeter of 36 inches.
The other rectangle has a length of 7.5 inches.
What is the perimeter of this rectangle?
27 in.

43. 1
Need Another Example?
2
3
4
Step-by-Step Example
2. In a scale drawing, the
perimeter of the garden
is 64 inches. The actual
length of AB is 18 feet.
What is the perimeter of
the actual garden?
The actual length is proportional to the length in the drawing with
a ratio of . Find the scale factor.
Convert feet to inches and divide out units.
Substitute. Then simplify.
perimeter of garden = perimeter of drawing • scale factor
P = 64 • 9 or 576
Find the perimeter of the actual garden.
The perimeter of the actual garden is 576 inches or 48 feet.

44. Answer
Need Another Example?
A model of a billboard has a side length of 3 inches.
The corresponding side on the actual billboard is 4 feet
long. The model has a perimeter of 42 inches. What is
the perimeter of the actual billboard?
672 in. or 56 ft

45. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
3. The Eddingtons have a
5-foot by 8-foot porch on
the front of their house.
They are building a
similar porch on the
back with double the
dimensions. Find the
area of the back porch.
The scale factor is 2.
Multiply by the square of the scale factor.
Evaluate the power.x = 40(4) or 160
The area of the front porch is (5)(8) or 40 square feet.
The back porch will have an area of 160 square feet.
x = 40(2)2

46. Answer
Need Another Example?
The Coopers bought a 6-foot by 9-foot
rectangular rug. They would like to buy a
similar rug with double the dimensions.
What will be the area of the new rug?
216 ft2