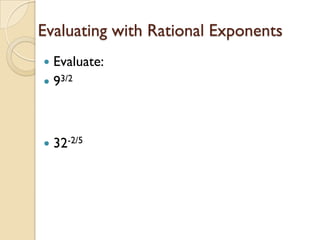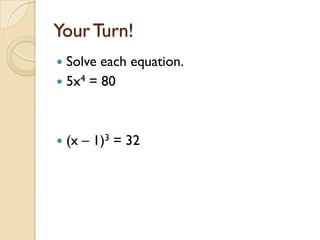The document discusses nth roots and rational exponents. It defines an nth root as the value that when raised to the nth power equals a given number. nth roots can be written using rational exponents, where the denominator is the index of the radical. If n is odd, there is one real nth root, and if n is even and the number is positive, there are two real nth roots. Examples are given of finding and evaluating nth roots and solving equations involving nth roots.

1. 7.1 nth Roots and Rational
Exponents

2. What is an “nth Root?”
 Extends the concept of square roots.
 For example:
◦ A cube root of 8 is 2, since 23 = 8
◦ A fourth root of 81 is 3, since 34 = 81
 For integers n greater than 1, if bn = a
then b is an nth root of a.
 Written where n is the index of the
radical.

3. Rational Exponents
nth roots can be written using rational
exponents.
 For example:
 In general, for any integer n
greater than 1.

4. Real nth Roots
 If n is odd:
◦ a has one real nth root

 If n is even:
◦ And a > 0, a has two real nth roots

◦ And a = 0, a has one nth root, 0

◦ And a < 0, a has no real nth roots


5. Finding nth Roots
Find the indicated real nth root(s) of a.
 Example: n = 3, a = -125
 n is odd, so there is one real cube root: (-
5)3 = -125
 We can write

6. Example:
 n = 4, a = 16
 n is even, and a > 0, so 16 has two real 4th
roots: 24 = 16 and (-2)4 = 16
 We can write

7. Your Turn!
 Find the indicated real nth root(s) of a.
 n = 4, a = 625
 n = 3, a = -27

8. Rational Exponents
 Not always of the form 1/n.


 The denominator of the exponent is the
index of the radical.

9. Evaluating with Rational Exponents
 Evaluate:
 93/2
 32-2/5

10. Your Turn!
 Evaluate:
 493/2
 16-3/4

11. Approximating with a Calculator
 Rewrite in rational exponent notation, then
use calculator.
 Example:
 Use ( ) around the exponent!
 Your Turn!
 Approximate

12. Solving Equations with nth Roots
 Get the power alone, then take nth roots
of both sides.
 Examples:
2x4 = 162 (x – 2)3 = 10

13. Your Turn!
 Solve each equation.
 5x4 = 80
 (x – 1)3 = 32