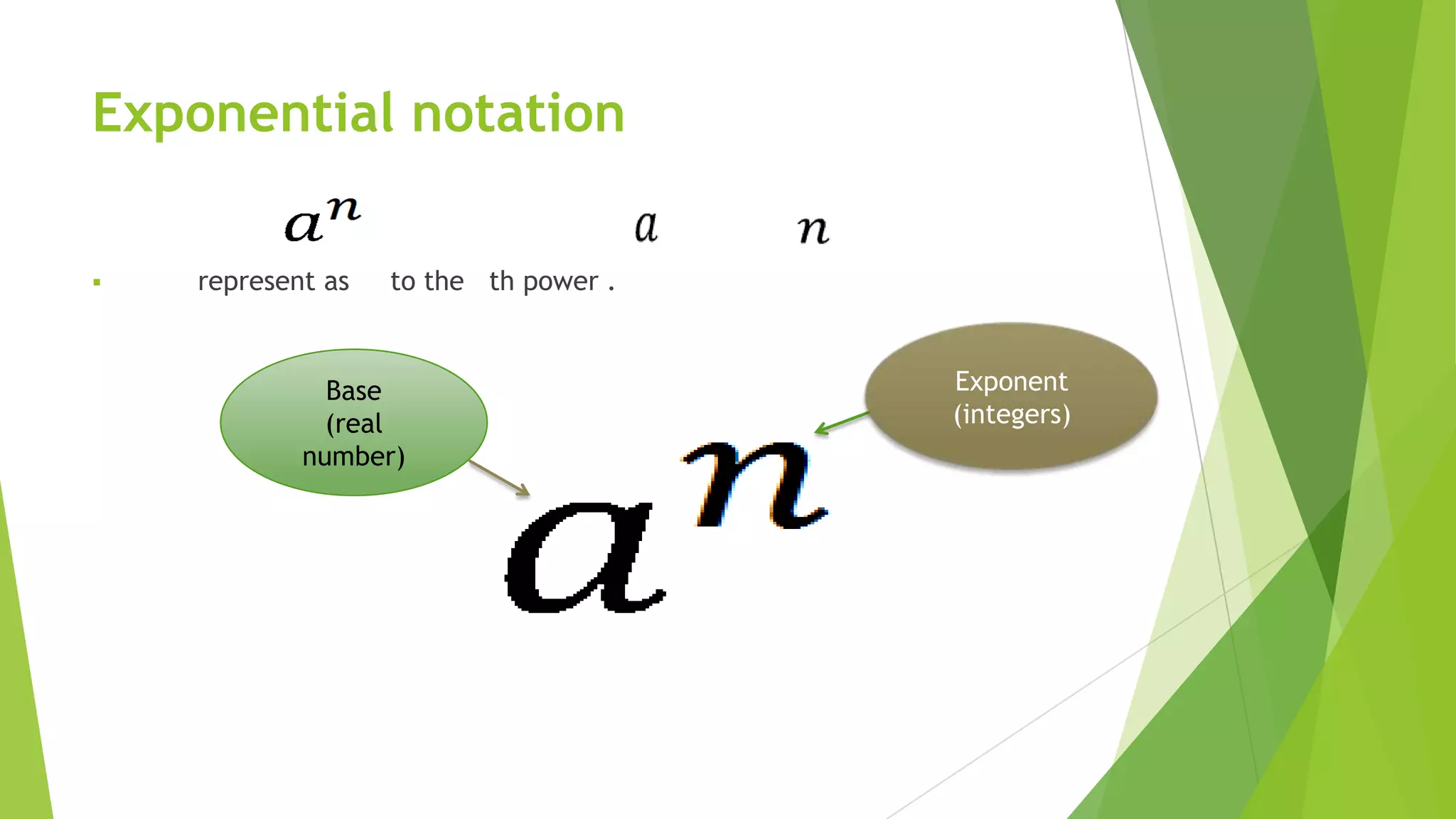
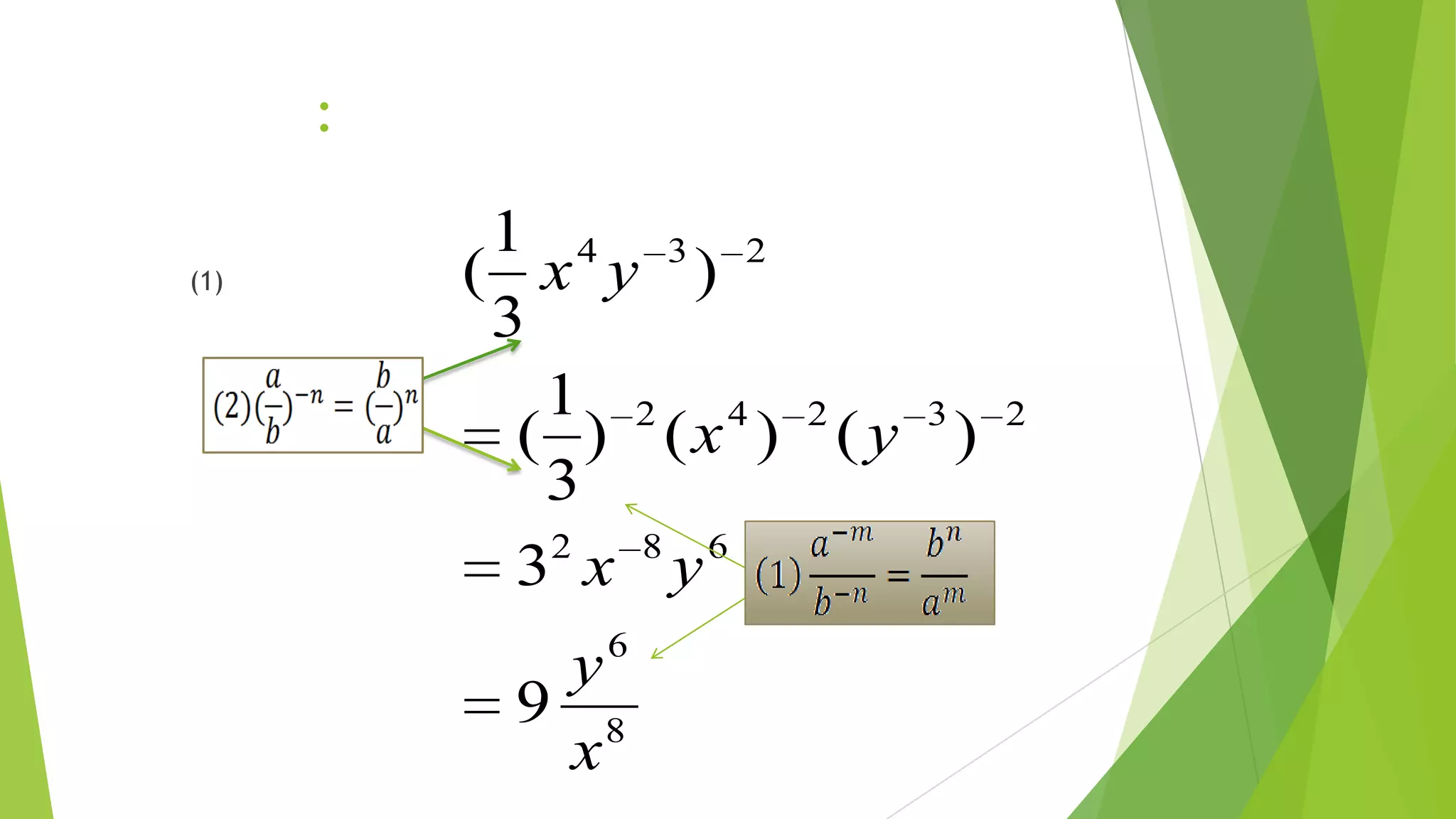
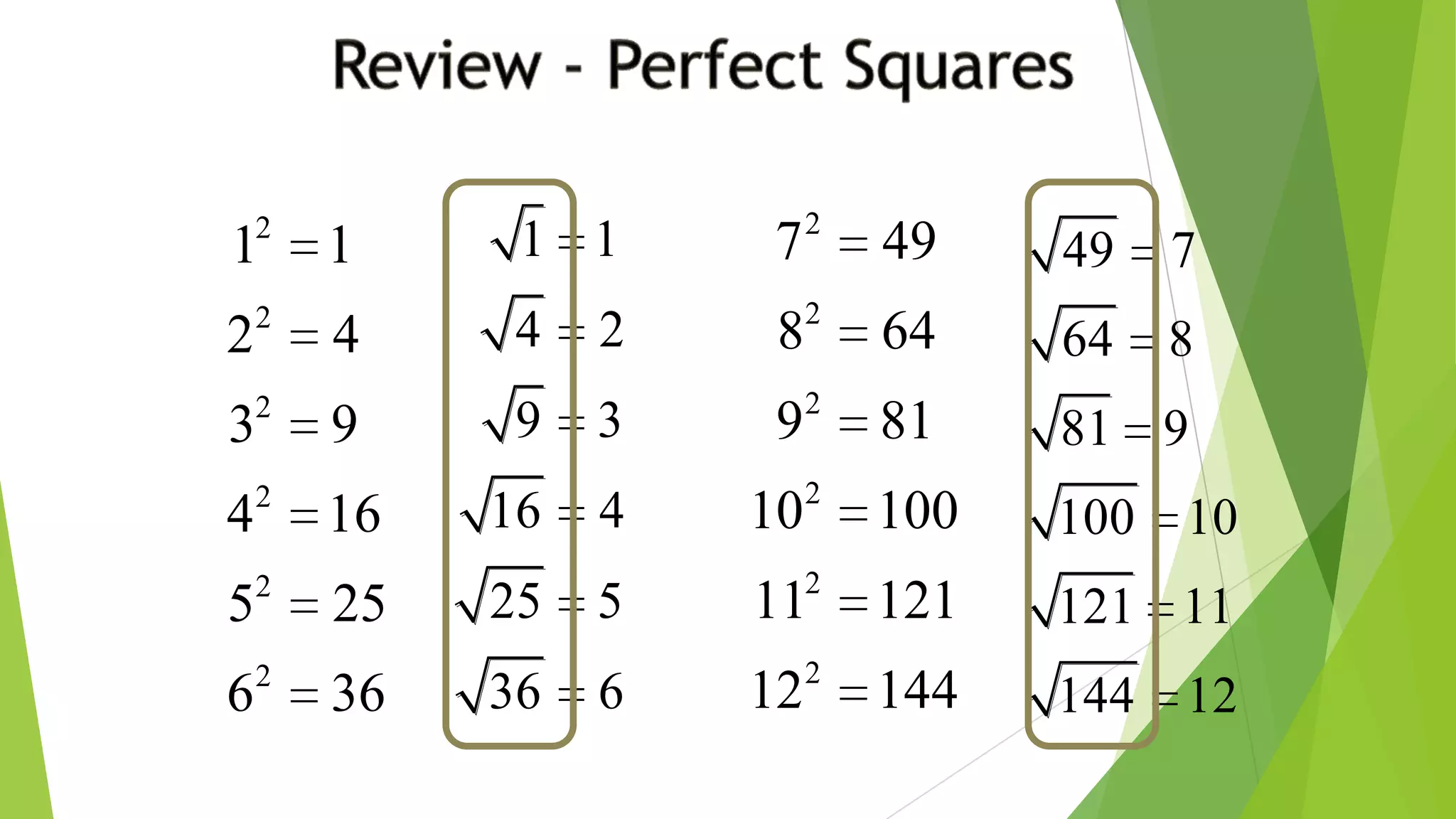
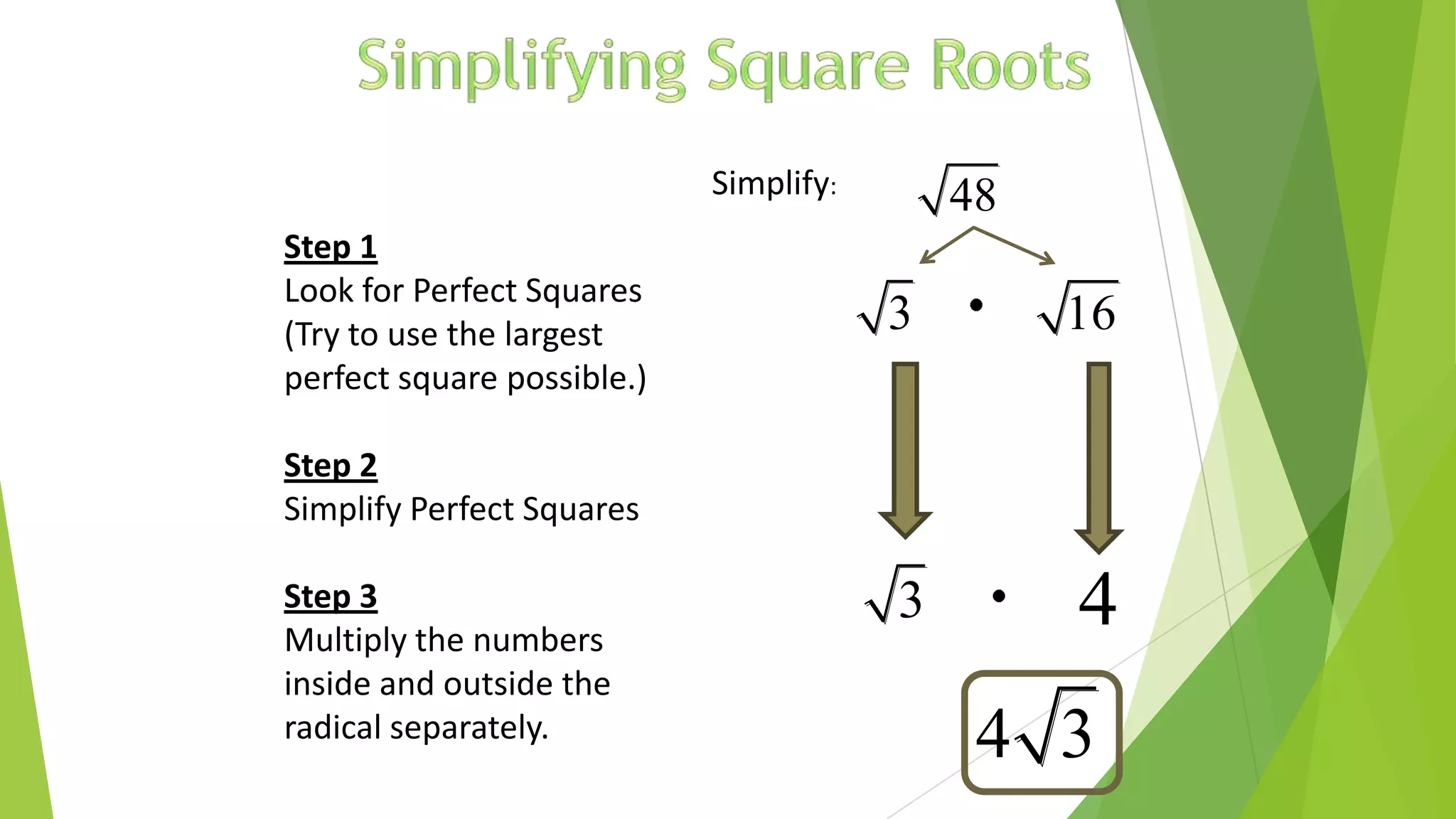
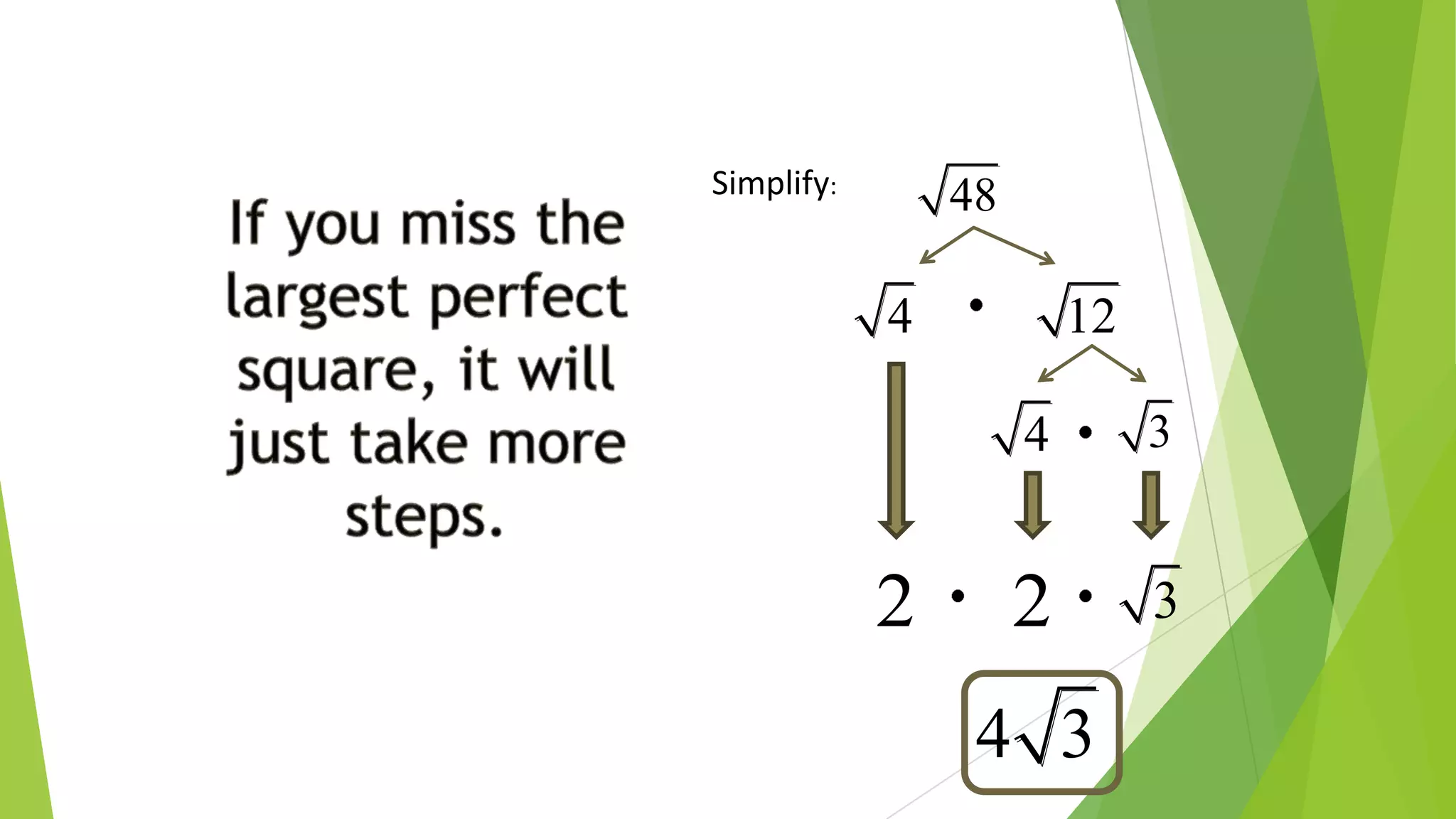
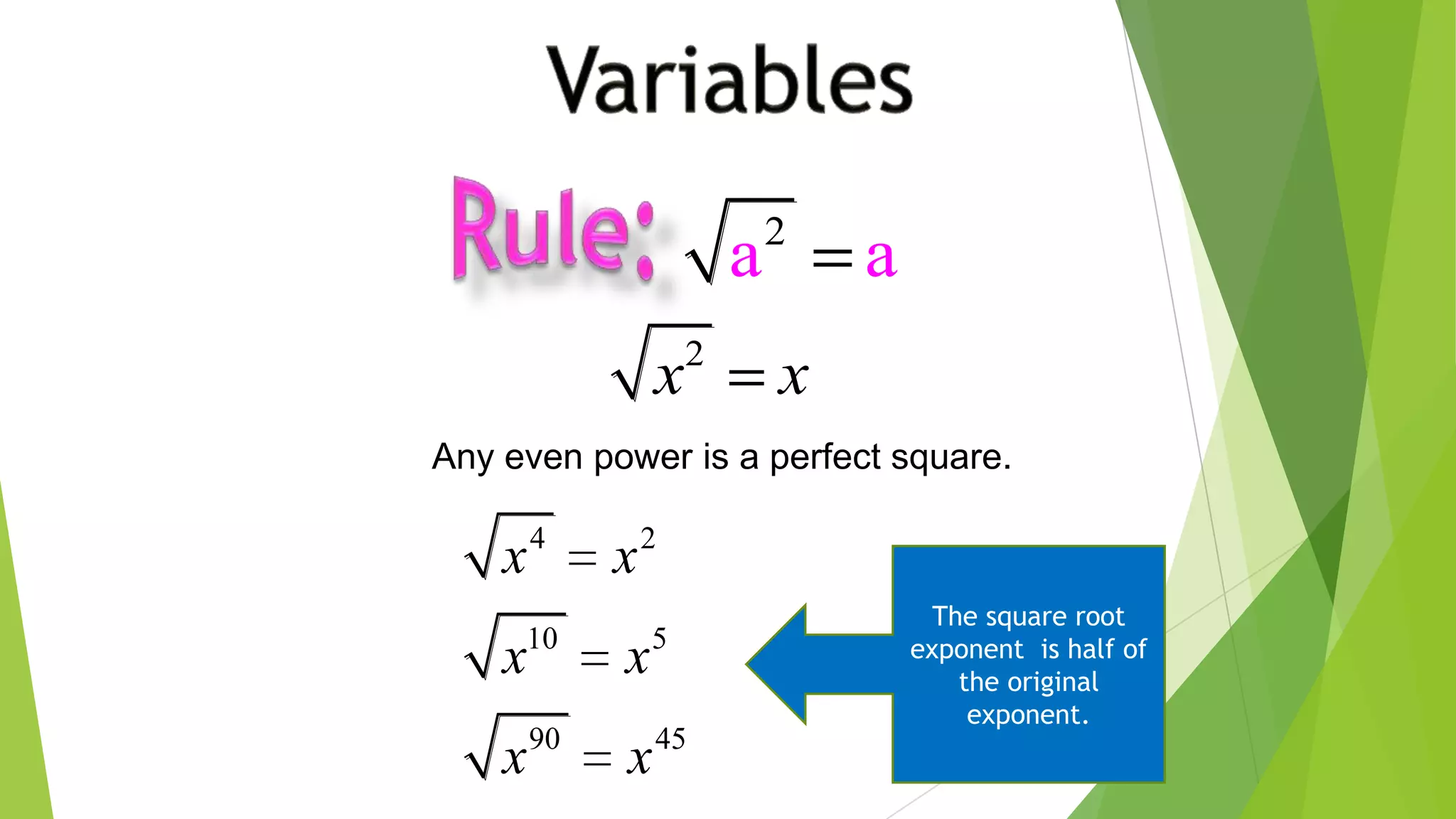
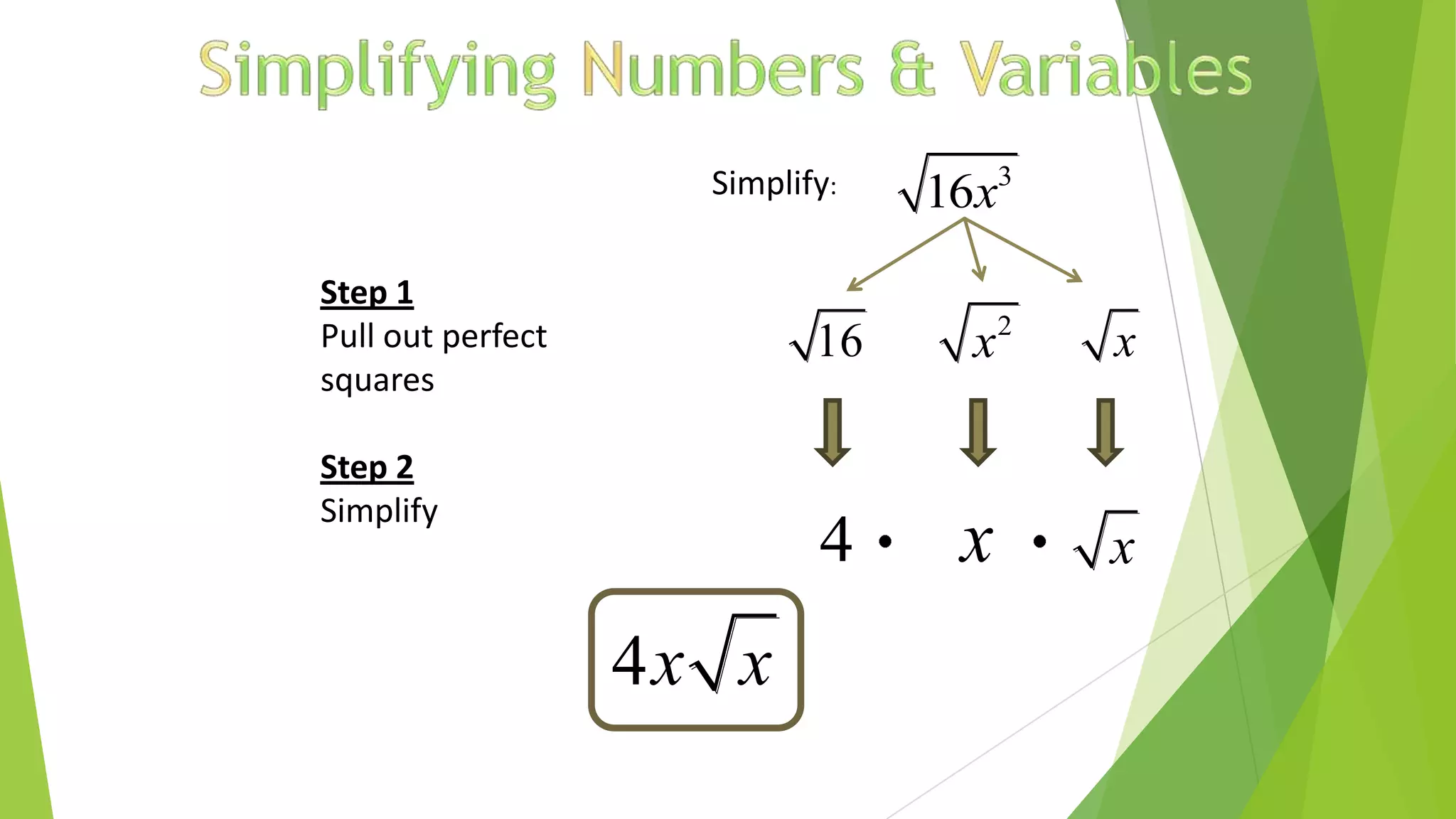
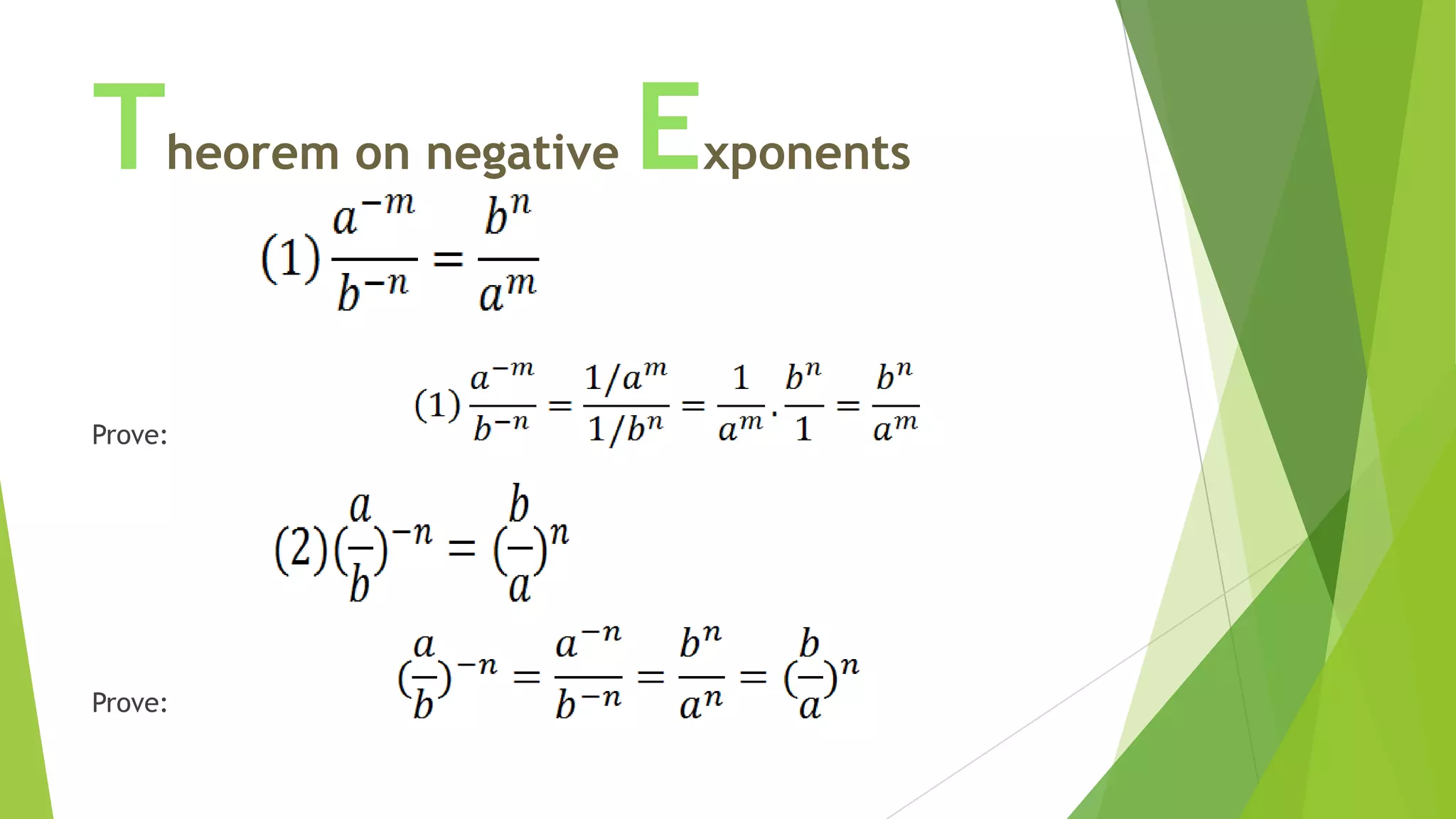This document discusses exponents, radicals, and nth roots. It defines exponential notation, laws of exponents, properties of radicals, and how to simplify expressions with exponents and radicals. It also explains what an nth root is, how to write nth roots using rational exponents, and how to determine the number of real nth roots a number has based on whether the index is odd or even. Examples are provided to illustrate how to solve equations and simplify expressions involving exponents, radicals, and nth roots.

1. Exponential &
Radicals
KUBHEKA SN

2. Exponential notation
 represent as to the th power .
Exponent
(integers)
Base
(real
number)

3. General case
(n is any positive integers)
Special cases
Zero and negative exponent
(where a c ≠ 0)
Example

4. Law of Exponents
Law Example

5. Theorem on negative Exponents
Prove:
Prove:

6. Example :
simplifying negative exponents
(1)
8
6
682
23242
234
9
3
)()()
3
1
(
)
3
1
(
x
y
yx
yx
yx

7. Principal nth root
Where n=positive integer greater than 1
= real number
Value for Value for
= positive real
number b
Such that
=negative real number
b
Such that

8. Properties of:
RADICAL
radicand
index
Radical
sign
PROPERTY EXAMPLE

9. Example:
combining radicalsQuestion:
12 5
12
5
12
5
3
2
4
1
4
1
3 2
4
1
1
3
2
α
α
αα
α
α
α
α
)(

10. Law of Radicals
law example
WARNING!

11. Simplifying Radicals
Operations with
Radicals

12. 2
2
2
2
2
2
1 1
2 4
3 9
4 16
5 25
6 36
1 1
4 2
9 3
16 4
25 5
36 6
2
2
2
2
2
2
7 49
8 64
9 81
10 100
11 121
12 144
49 7
64 8
81 9
100 10
121 11
144 12

13. 2
1) a a
b) a2 ba
3)
a
b b
a

14. Simplify:
Step 1
Look for Perfect Squares
(Try to use the largest
perfect square possible.)
Step 2
Simplify Perfect Squares
Step 3
Multiply the numbers
inside and outside the
radical separately.
48
3 16
43
4 3

15. Simplify:
48
4 12
34
2 2 3
4 3

16. 2
a a
2
x x
Any even power is a perfect square.
4 2
10 5
90 45
x x
x x
x x
The square root
exponent is half of
the original
exponent.

17. Odd powers
When you take the square root of an odd power, the result is always an even
power and one variable left inside the radical.
5 2
11 5
91 45
x x x
x x x
x x x

18. Simplifying using variables
When you simplify an even power of a variable and the result is an odd power,
use absolute value bars to make sure your answer is positive.
14 7
14 12 7 6
x x
x y x y
Even powers
do not need
absolute
value.

19. Simplify: 3
16x
Step 1
Pull out perfect
squares
Step 2
Simplify
16 2
x x
x4 x
4x x

20. a ab b
You can only multiply radicals by other radicals
8 3
Both under the radical
CAN multiply
8 3
Not under the radical
CANNOT multiply

21. What is an “nth Root?”
 Extends the concept of square roots.
 For example:
 A cube root of 8 is 2, since 23 = 8
 A fourth root of 81 is 3, since 34 = 81
 For integers n greater than 1, if bn = a then b is an nth root of a.
 Written where n is the index of the radical.

22. Rational Exponents
 nth roots can be written using rational exponents.
 For example:
 In general, for any integer n greater than 1.

23. Real nth Roots
 If n is odd:
a has one real nth root

 If n is even:
And a > 0, a has two real nth roots

And a = 0, a has one nth root, 0

And a < 0, a has no real nth roots


24. Finding nth Roots
Find the indicated real nth root(s) of a.
 Example: n = 3, a = -125
 n is odd, so there is one real cube root: (-5)3 = -125
 We can write

25. Your Turn!
 Solve each equation.
 5x4 = 80
 (x – 1)3 = 32

26. http://www.slideshare.net/nurulatiyah/radical-and-exponents-
2?qid=b15cb847-ee58-4b34-aaba-
ce8e8ab498a5&v=default&b=&from_search=10
http://www.slideshare.net/holmsted/roots-and-radical-
expressions?qid=b15cb847-ee58-4b34-aaba-
ce8e8ab498a5&v=default&b=&from_search=12
http://www.slideshare.net/hisema01/71-nth-roots-and-rational-
exponents?qid=b15cb847-ee58-4b34-aaba-
ce8e8ab498a5&v=default&b=&from_search=15