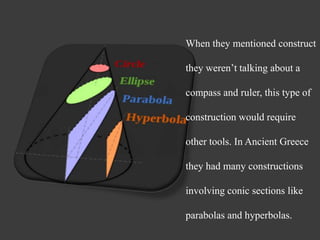
The document provides a history of solving cubic equations from ancient Greece to modern times. It describes how Greek mathematicians were trying to construct an angle one-third the size of a given angle, which led to the development of trigonometry and cubic equations. Several mathematicians, including Al-Khayammi, Del Ferro, Tartaglia, and Cardano, made discoveries in solving cubic equations. The document then explains how to derive the formula for solving cubic equations by finding the "depressed cubic" without the quadratic term, and uses the quadratic formula to solve for the solutions.

1. By: Jenissa Reynoso

2. Introduction
 The following slides explains how to solve a cubic
equation
 To start off I’m going to give you a brief cool history of
the cubic equation
 Then I’ll explain how to find the depressed cubic equation
which will help get to the solution

3. History of the cubic equation
 The cubic equation goes as far back to 400 B.C, the birth
of this problem came from a geometric question from
Greek mathematicians. The question was the following
, “Given an angle, is there a way to construct an angle one
third as large?”

4. When they mentioned construct
they weren’t talking about a
compass and ruler, this type of
construction would require
other tools. In Ancient Greece
they had many constructions
involving conic sections like
parabolas and hyperbolas.

5. History of the cubic equation
 Once trigonometry came along the mathematicians came up with a
way of solving the cubic equation. Finding x amounts to solving this
equation.
 To find one third of the given angle (theta) ᶿ, we can begin by thinking of
(theta) ᶿas three times the angle we’re looking for, which we’ll call (alpha) α;
that is, α = θ/3 . Now we apply the formula for the cosine of 3α:
Since the angle (theta) ᶿis known, we also know cos(θ); call it a. To construct
θ/3 , we need to construct its cosine. If we let then using the formula
above with α = θ/3 , we get

6. History of the cubic equation
 After mathematicians knew about this equation
the first to attempt to solve it was Al-
Khayammi, he thought he had it all figured out
but when he tried using actual numbers his
method was no help at all and he admitted to it.

7. Many mathematicians had a
lot of trouble figuring out how
to solve a cubic equation until
Scipione Del Ferro (1465-
1526) and Niccolo Fontana
(Tartaglia) (1500 – 1557)
from Italy came in the picture.

8. History of the cubic equation
 They both discovered how to solve a cubic equation and kept it a
secret in order to challenge other people. The person Ferro passed
the secret to one of his students Antonio Maria Fiore, who
challenged Tartaglia in a competition. They both had different
ways of solving the cubic equation but were both correct.

9. History of the cubic equation
 However Tartaglia beat Fiore and once the news was out about the
competition Cardano wanted to meet Tartaglia to get the secret
from him which he did after convincing Tartaglia that he would
keep it a secret also. His secrecy didn’t last for long because he
wanted to publish this solution, in order to not break his promise of
secrecy he used Fiore’s way of solving the cubic equation.

10. History of the cubic equation
 Cardano assistant Ferrari figured out how to
solve the equation of degree four (the
quartic) and Cardano published a book called
Arc Magna meaning “The great Art”
revealing the solution to the cubic equation
and quartic equation.

11. There was one mistake that
Cardano had in his method
which was later on resolved
by Bombelli, all he did was
use the square root of
negative numbers as
possible solutions. The cubic
equation is one of the
mathematical problems that
led to the development of
abstract algebra.

12. How does one find the formula
for the solution of the cubic?
 To find the solution to the cubic equation we first have to find the
formula in other words we have to find the cubic equation without
a square term sometimes called “depressed cubic”.We start with
the complete cubic equation which is:

13. How does one find the formula
for the solution of the cubic?
 if the cubic equation doesn’t have one as a leading coefficient just
divide both sides of the equation by that leading coefficient and
you’ll end up with one as a leading coefficient. Then we continue
with the first substitution:
 Let
 when we substitute this into the equation we end up with:

14. How does one find the formula
for the solution of the cubic?
 Now we need to expand these terms:
 (Cubic term):
 (Quadratic term):
 (Linear term):
 (Constant):

15. How does one find the formula
for the solution of the cubic?
 Once we expanded these terms we simplify them:

16. How does one find the formula
for the solution of the cubic?
 Then we gather like term we end up with:
 We substitute again we let and
 this is how we get the cubic equation without a square term
sometimes called “depressed cubic” which is:

17. The solution for the cubic
equations
 Since we have the depressed cubic equation like our little face as
shown, we can now find the solution :

18.  We let
 After substituting and simplifying the
equation we end up with :

19. The solution for the cubic
equations
 Then we multiply by which gives us:
 this is a quadratic in z^3
 We plug into the quadratic formula
 Once we find the solution to the quadratic equation we substitute
back to get the solution for x.

20. Extra help!!!
 If you need any
extra help please
feel free to e-mail
me at
reynosje@kean.edu
or ask after class for
additional help I’ll be
happy to help.
 Just remember Math
is awesome!!!