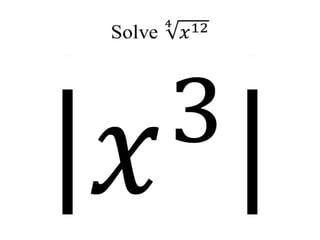1) The document discusses evaluating nth roots of numbers and expressions, including square roots, cube roots, and nth roots. 2) It provides definitions and examples of even and odd roots of positive and negative numbers. Even roots of negative numbers are undefined, while odd roots of negative numbers are negative. 3) Methods are described for evaluating nth roots of monomial expressions by splitting them into factors and taking the nth root of each factor.

1. 6-1 Nth Roots
Objective: To simplify radicals
having various indices, and to use a
calculator to estimate the roots of
numbers.

2. Square Roots
What power is a square root?
A square is the inverse of a square root…
3
3 ?

3. Square Root*
Definition: For any real numbers a and b, if
2
a b then a is a square root of b or
b a
We can also write square roots using the ½
power.
1
2
b
b

4. Cube Root*
Definition: For any real numbers a and b, if
3
a b then a is a cube root of b or
3
b a
We can also write cube roots using the 1/3
power.
1
3
3
b
b

5. nth Root*
Definition: For any real numbers a and b, if
n
a b then a is a nth root of b or
n
b a
1
We can also write nth roots using the power.
n
b
1
n
n
b

6. Examples: Roots (of powers of 2)
Even Roots:
Odd Roots:
4 2
4
6
8
3
8
16 2
5
32
64 2
7
128
2
256 2
9
512
2
2
2

7. Roots of negative numbers*
Even roots: Negative numbers have no
even roots. (undefined)
Odd Roots: Negative numbers have
negative roots.
4
3
27
undefined
3

8. Examples: Roots (of powers of 2)
Even Roots:
4
undef .
Odd Roots:
3
8
2
4
16
undef .
5
32
6
64
undef .
7
128
2
9
512
2
8
256
undef .
2

9. Roots: Number and Types
Even Roots
Positive
2 (one positive, one 1 (positive)
negative)
64
Negative
Odd Roots
0 (undefined)
64
3
8
undef .
64
4
1 (negative)
3
64
4

10. MORE EXAMPLES
if n (index) is an even integer
if n is an odd integer
a<0 has no real nth roots
a<0 has one real nth root
2 16
a=0 has one real nth root
4i (not a realsolution)
3 8
a=0 has one real nth root
2
a>0 has two possible real nth roots
a>0 has one real nth roots
40
4
x
32
4 32
30
0
24 2
0
3 27
3

11. Odd Roots (of variable
expressions)*
When evaluating odd roots (n is odd) do not
use absolute values.
3
5
a
3
3
a
15
a
a
3
243 7
5
32
2

12. Evaluating Roots of Monomials
To evaluate nth roots of monomials:
(where c is the coefficient, and x, y and z are
variable expressions)
n
cxyz
n
c
n
1
n
x
n
1
n
y
n
1
n
z
(c ) ( x ) ( y ) ( z )
1
n
or
• Simplify coefficients (if possible)
• For variables, evaluate each variable separately

13. Evaluating Roots of Monomials*
To find a root of a monomial
• Split the monomial into a product of the factors,
and evaluate the root of each factor.
• Variables: divide the power by the root
Coefficients: re-write the number as a product
of prime numbers with powers, then divide the
powers by the root.
49 x 8
5
32 x10 y15
49 x 8
5
25
72
5
( x 2 )5
( x 4 )2
5
7x4
( y 3 )5
2x2 y3