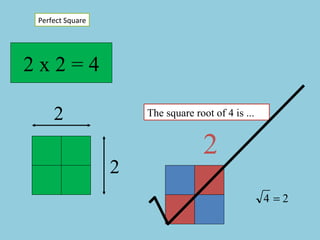
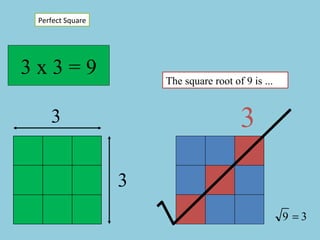
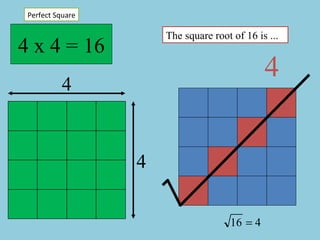
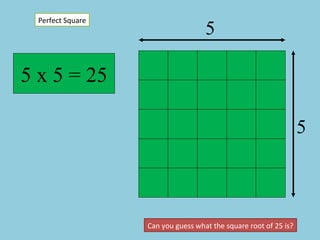
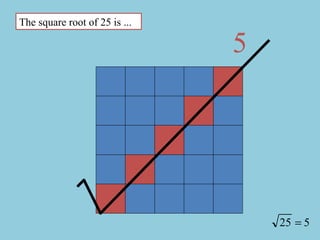
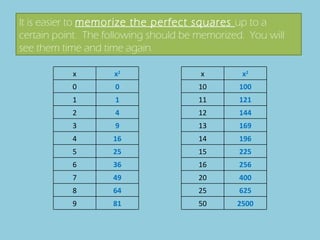
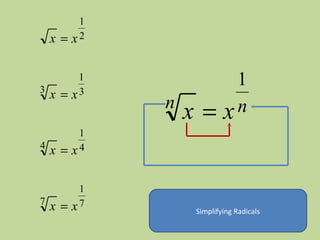
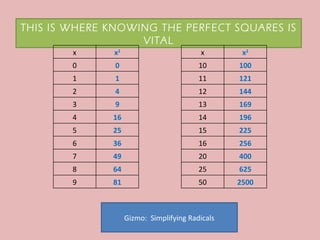
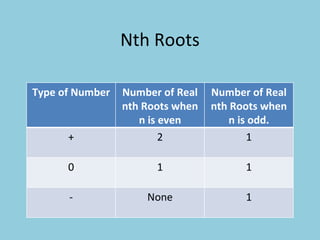
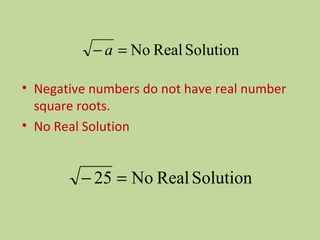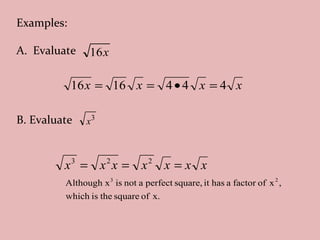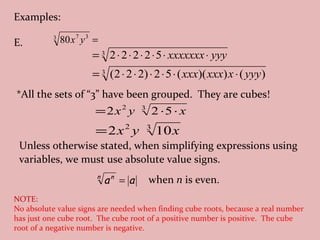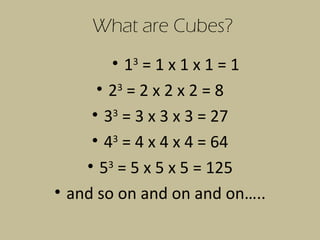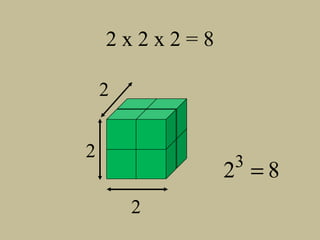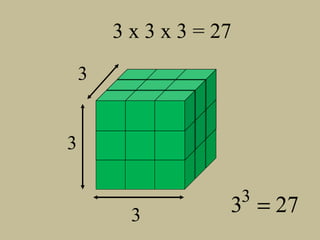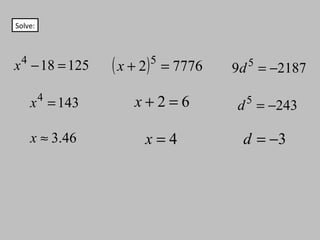- The document discusses perfect squares, square roots, cubes, and nth roots. - It provides examples of finding square roots and cube roots of various numbers. - Key formulas introduced include the volume of a sphere and estimating distance to the horizon.

1. Radicals Module 14 Topic 1

2. What are Perfect Squares? 1 • 1 = 1 2 • 2 = 4 3 • 3 = 9 4 • 4 = 16 5 • 5 = 25 6 • 6 = 36 49, 64, 81, 100, 121, 144, ... and so on….

3. Since , . Finding the square root of a number and squaring a number are inverse operations. To find the square root of a number n , you must find a number whose square is n. For example, is 7 , since 7 2 = 49. Likewise, (–7) 2 = 49, so –7 is also a square root of 49. We would write the final answer as: The symbol, , is called a radical sign. An expression written with a radical sign is called a radical expression . The expression written under the radical sign is called the radicand .

4. NOTE : Every positive real number has two real number square roots. The number 0 has just one square root, 0 itself. Negative numbers do not have real number square roots. When evaluating we choose the positive value of a called the principal root . Evaluate Notice, since we are evaluating, we only use the positive answer.

5. For any real numbers a and b , if a 2 = b , then a is a square root of b . Just like adding and subtracting are inverse operations, finding the square root of a number and squaring a number are inverse operations.

6. 2 2 2 x 2 = 4 Perfect Square The square root of 4 is ... 2

7. 3 x 3 = 9 3 3 Perfect Square The square root of 9 is ... 3

8. 4 x 4 = 16 4 4 Perfect Square 4 The square root of 16 is ...

9. 5 5 5 x 5 = 25 Perfect Square Can you guess what the square root of 25 is?

10. 5 The square root of 25 is ...

11. This is great, But…. Do you really want to draw blocks for a problem like… probably not! If you are given a problem like this: Find Are you going to have fun getting this answer by drawing 2025 blocks? Probably not!!!!!!

12. It is easier to memorize the perfect squares up to a certain point. The following should be memorized. You will see them time and time again. x x 2 x x 2 0 0 10 100 1 1 11 121 2 4 12 144 3 9 13 169 4 16 14 196 5 25 15 225 6 36 16 256 7 49 20 400 8 64 25 625 9 81 50 2500

13. To name the negative square root of a , we say To indicate both square roots, use the plus/minus sign which indicates positive or negative.

14. Simplifying Radicals

15. Negative numbers do not have real number square roots. No Real Solution

16. = b This symbol represents the principal square root of a . The principal square root of a non-negative number is its nonnegative square root. Gizmo: Square Roots

17. Simplifying Radicals Divide the number under the radical. If all numbers are not prime, continue dividing. Find pairs, for a square root, under the radical and pull them out. Multiply the items you pulled out by anything in front of the radical sign. Multiply anything left under the radical . It is done!

18. Evaluate the following: To solve: Find all factors Pull out pairs (using one number to represent the pair. Multiply if needed)

19. Find all real roots :

20. To find the roots, you will need to simplify radial expressions in which the radicand is not a perfect square using the Product Property of Square Roots. Not all numbers are perfect squares

21. THIS IS WHERE KNOWING THE PERFECT SQUARES IS VITAL Gizmo: Simplifying Radicals x x 2 x x 2 0 0 10 100 1 1 11 121 2 4 12 144 3 9 13 169 4 16 14 196 5 25 15 225 6 36 16 256 7 49 20 400 8 64 25 625 9 81 50 2500

22. Examples: Simplify Steps Explanation

23. B. Simplify Steps Explanation

24. The general rule for reducing the radicand is to remove any perfect powers. We are only considering square roots here, so what we are looking for is any factor that is a perfect square. In the following examples we will assume that x is positive. Gizmo: Simplifying Radicals

25. Examples: A. Evaluate B. Evaluate

26. Examples: C. Evaluate D. Evaluate

27. Examples: E. Unless otherwise stated, when simplifying expressions using variables, we must use absolute value signs. when n is even. *All the sets of “3” have been grouped. They are cubes! NOTE: No absolute value signs are needed when finding cube roots, because a real number has just one cube root. The cube root of a positive number is positive. The cube root of a negative number is negative.

28. Evaluate the following: No real roots

29. What are Cubes? 1 3 = 1 x 1 x 1 = 1 2 3 = 2 x 2 x 2 = 8 3 3 = 3 x 3 x 3 = 27 4 3 = 4 x 4 x 4 = 64 5 3 = 5 x 5 x 5 = 125 and so on and on and on…..

30. 1 2 3 4 5 6 7 8 Cubes

31. 2 2 2 2 x 2 x 2 = 8

32. 3 x 3 x 3 = 27 3 3 3

33. N th Roots When there is no index number, n , it is understood to be a 2 or square root. For example: = principal square root of x. Not every radical is a square root. If there is an index number n other than the number 2, then you have a root other than a square root.

34. Since 3 2 = 9. we call 3 the square root of 9. Since 3 3 =27 we call 3 the cube root of 27. Since 3 4 = 81, we call 3 the fourth root of 81. N th Roots

35. More Explanation of Roots This leads us to the definition of the n th root of a number. If a n = b then a is the n th root b notated as, .

36. N th Roots Since (-)(-) = + and (+)(+) = + , then all positive real numbers have two square roots. Remember in our Real Number System the is not defined. However we can find the cube root of negative numbers since (-)(-)(-) = a negative and (+)(+)(+) = a positive. Therefore, cube roots only have one root .

37. Nth Roots Type of Number Number of Real nth Roots when n is even Number of Real nth Roots when n is odd. + 2 1 0 1 1 - None 1

38. Nth Roots of Variables Lets use a table to see the pattern when simplifying nth roots of variables. *Note: In the first row above, the absolute value of x yields the principal root in the event that x is negative.

39. Examples: Find all real cube roots of -125, 64, 0 and 9. Find all real fourth roots of 16, 625, -1 and 0. As previously stated when a number has two real roots, the positive root is called the principal root and the Radical indicates the principal root. Therefore when asked to find the nth root of a number we always choose the principal root.

40. F. Write each factor as a cube. Write as the cube of a product. Simplify. Absolute Value signs are NOT needed here because the index, n, is odd.

41. Application/Critical Thinking The formula for the volume of a sphere is . Find the radius, to the nearest hundredth, of a sphere with a volume of . A student visiting the Sears Tower Skydeck is 1353 feet above the ground. Find the distance the student can see to the horizon. Use the formula to the approximate the distance d in miles to the horizon when h is the height of the viewer’s eyes above the ground in feet. Round to the nearest mile. A square garden plot has an area of . a. Find the length of each side in simplest radical form. b. Calculate the length of each side to the nearest tenth of a foot.

42. Application Solutions: A. B. C.

43. Evaluate the following: To solve: Find all factors Pull out set’s that contain the same number of terms as the root (using one number to represent the set of 4. Multiply if needed)

44. Evaluate the following: No real roots

45. Practice Problems and Answers

46. Solving Equations When solving equations with exponents, you must isolate the variable (with the exponent). Then you must take the appropriate root of both sides of the equation. Since the square and the square root are inverse operations, they cancel each other, as can bee seen on the left side of the equation. To check your solutions: Plug both answers into the original equation. Both answers, 6 and -6, work.

47. Alternative Method If you did, you found that for the equation, , -4 does NOT work!!!!!!! When you plug in -4 for n, you get – 7168, which is not what was given in the equation. So, n = 4 works, n = -4 does not. The solution is n = 4 and the extraneous solution is n = -4. Extraneous solutions do not satisfy original equation and must be discarded. Did you check your answers by plugging both answers into the original equation. Did you check your answers by plugging both answers into the original equation.

48. Solve:

49. The following equation is used by ABC Toys to determine how many pieces of a specific round toy will fit into a shipping crate. Find the approximate radius of each toy, rounded to the nearest hundredths, if you know that there are 50 toys in the box. Multiply both sides by 8 to get rid of the fraction. Divide both sides by 3∏ Take the cube root of both sides Round to the correct place value Plug in what you know

50. A square piece of land is being turned into a skate park. The area of the land piece is 189 ft 2 . a) Find the length of each side in simplest radical form. b) Calculate the length of each side to the nearest tenth of a foot. Find the length of each side in simplest radical form. The area of a square is found by using the equation, A =s 2 . Plug in what you know, and solve for s. b) Calculate the length of each side to the nearest tenth of a foot. 13.7 ft 13.7 ft