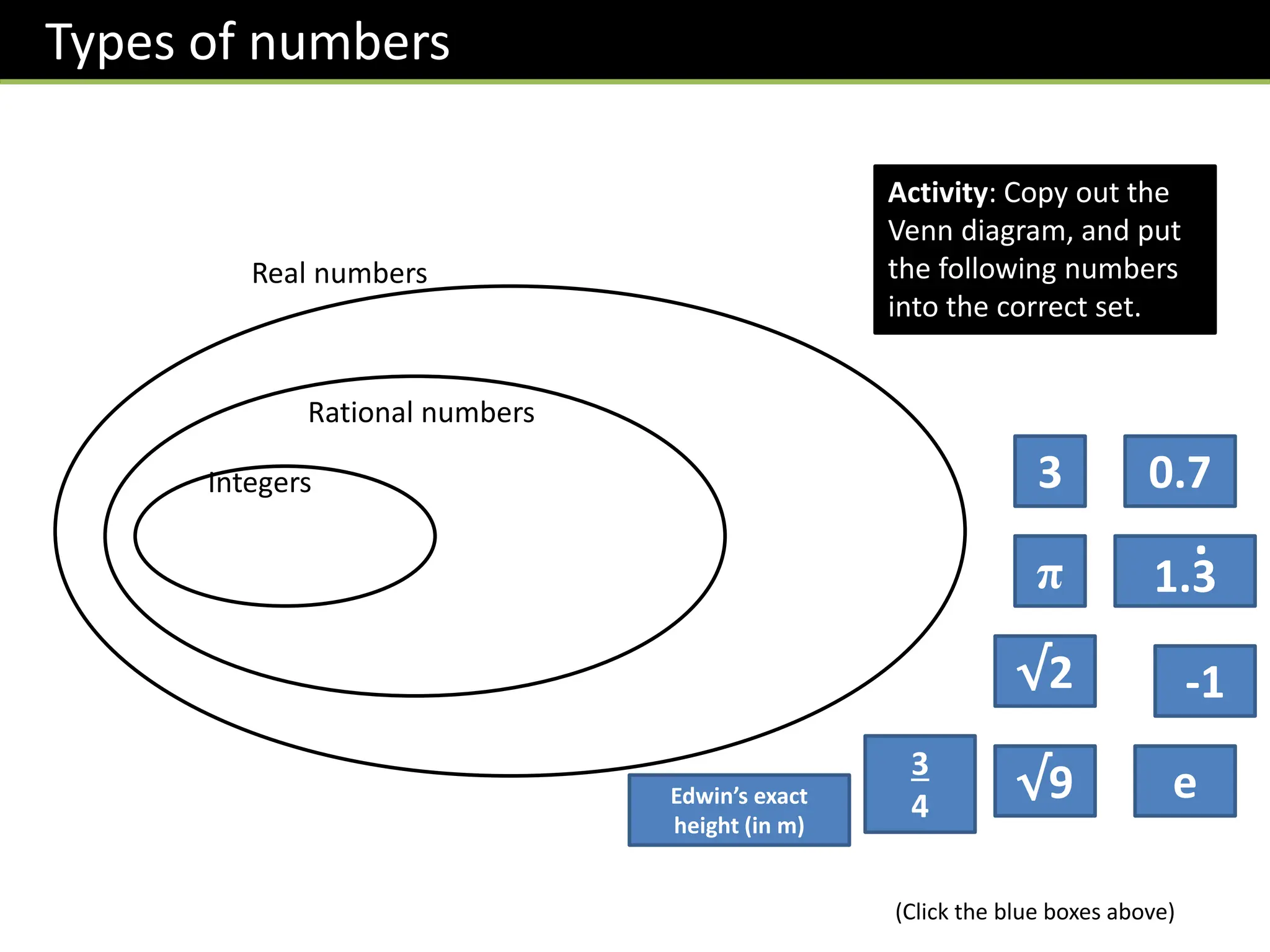
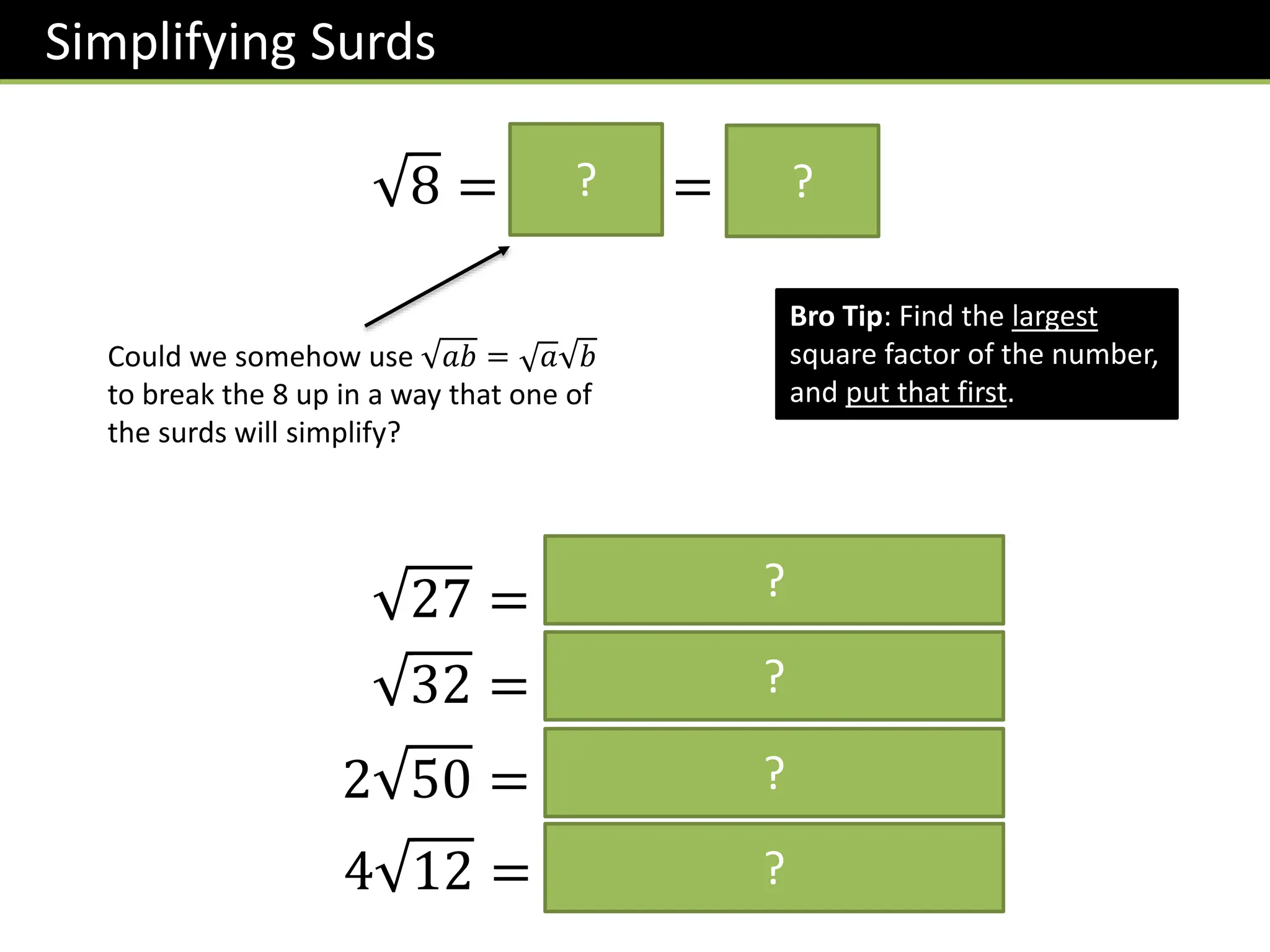
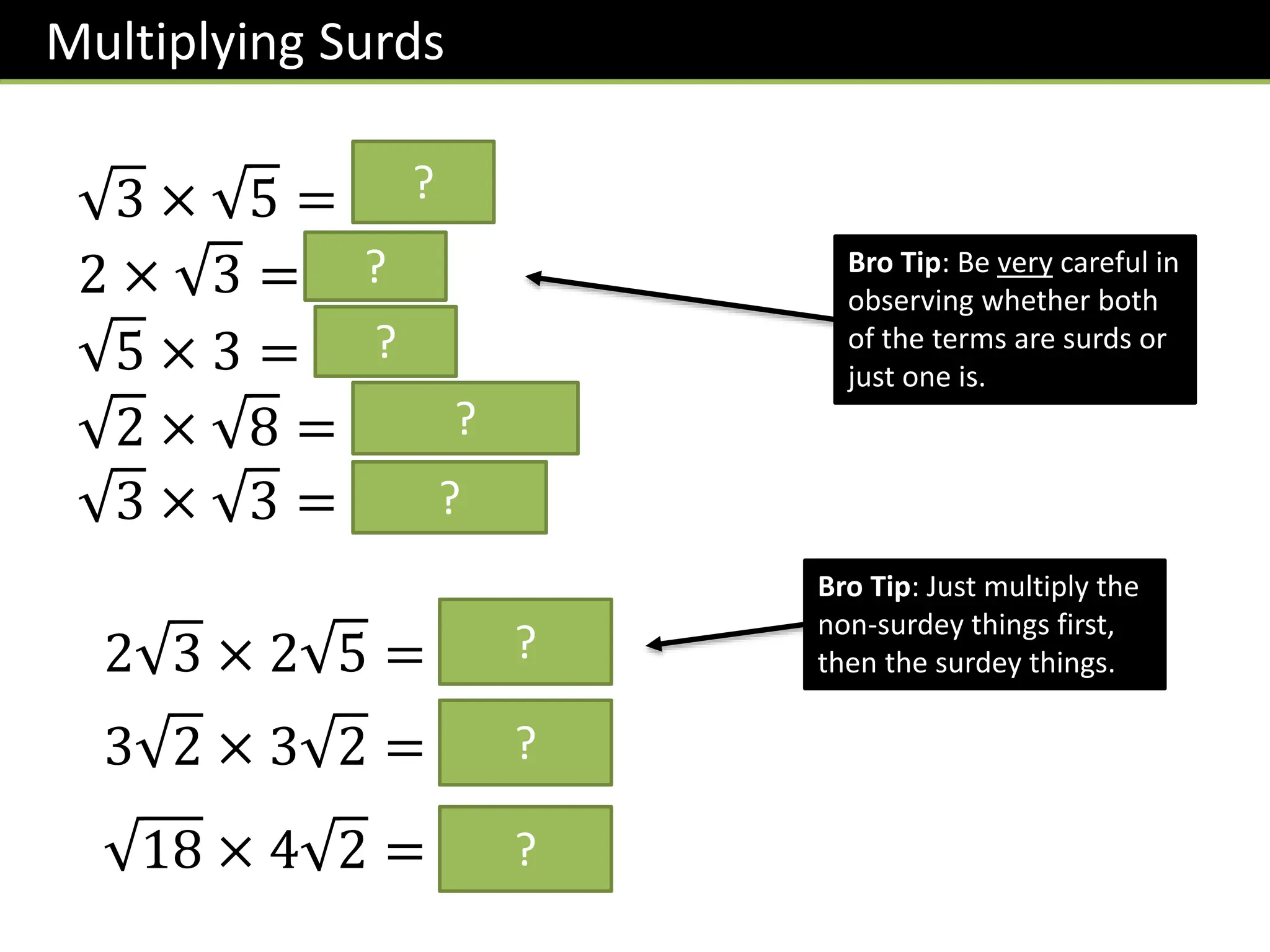
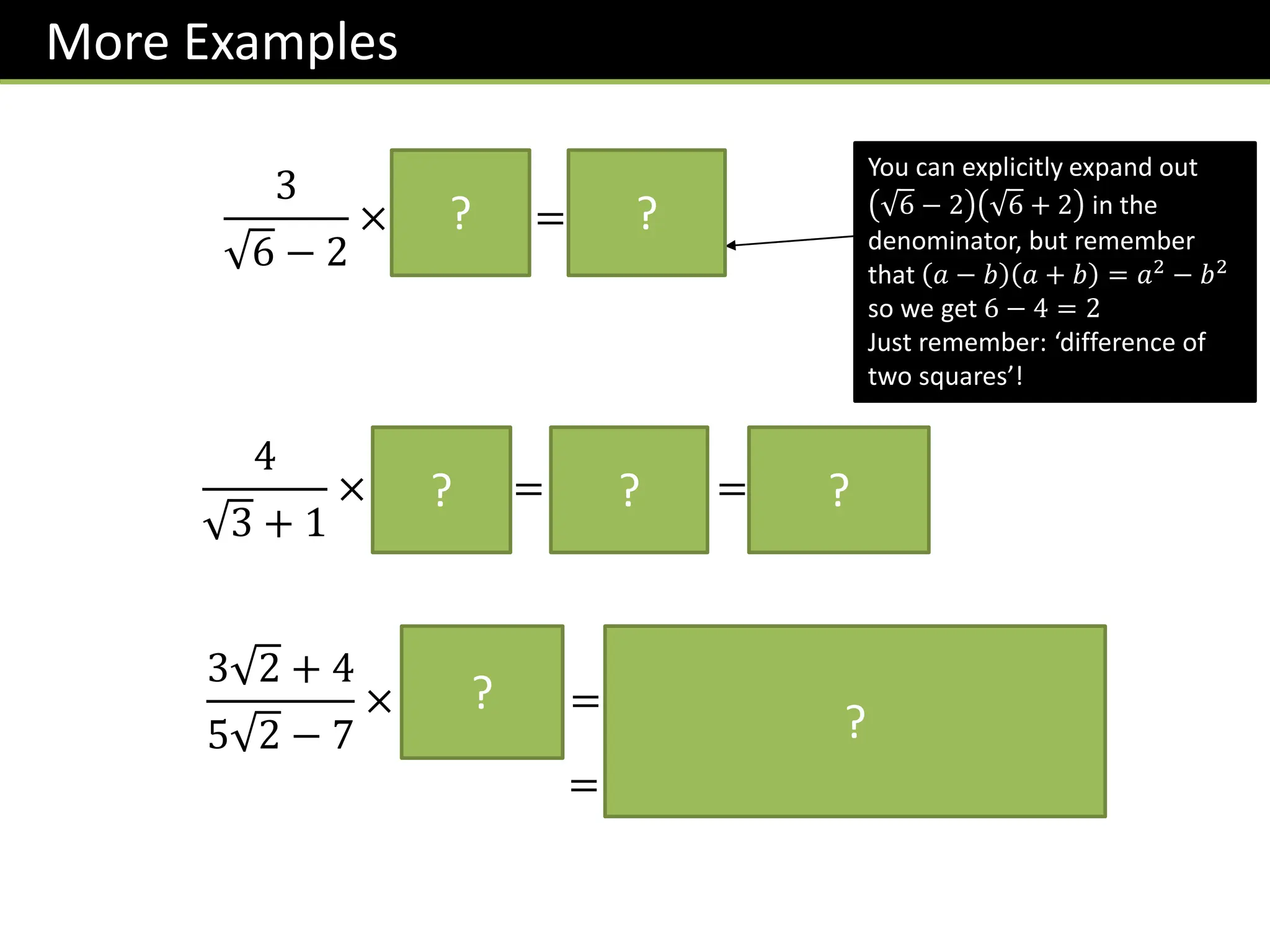
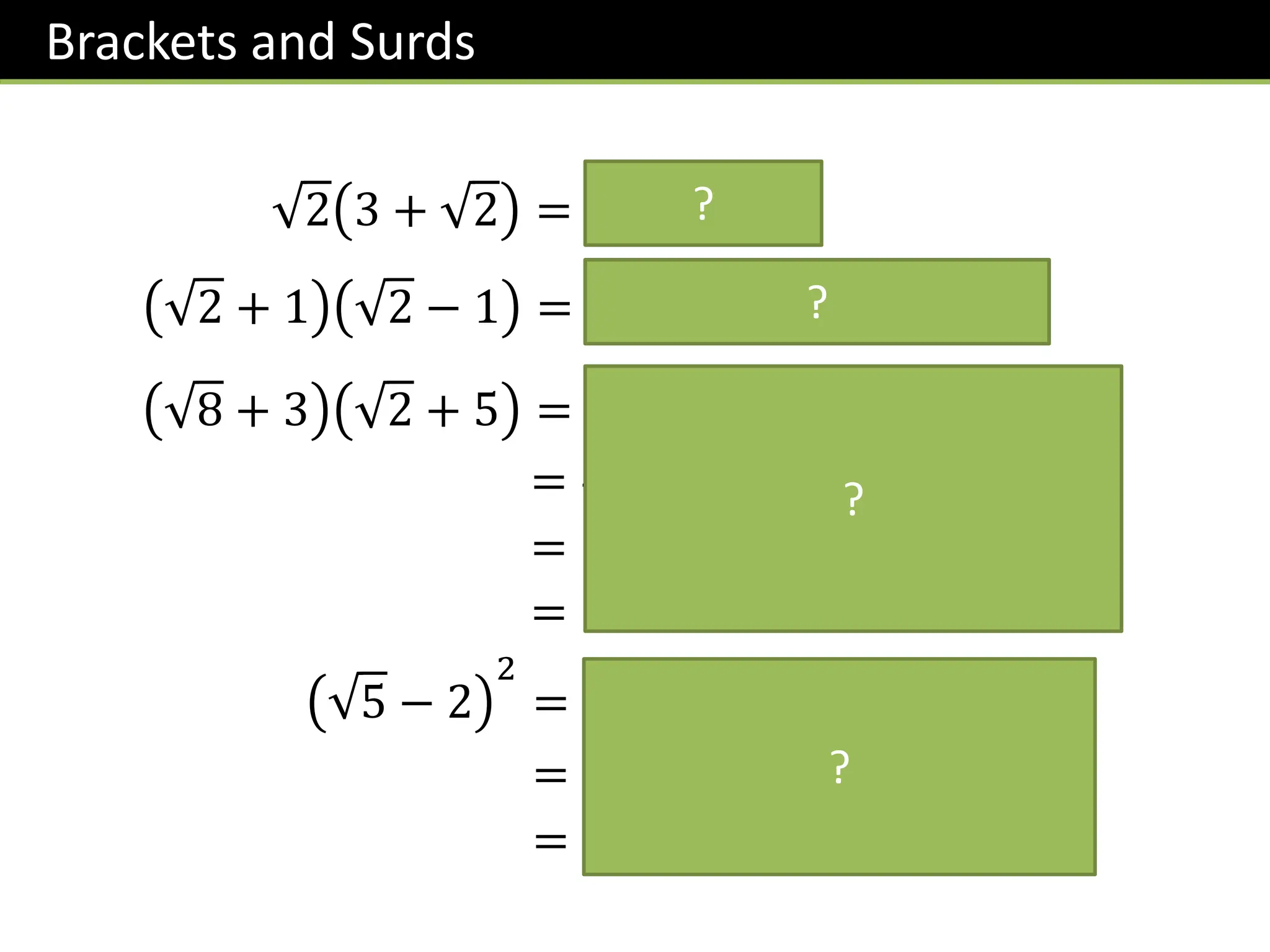The document provides a detailed overview of surds, including definitions, laws, simplification techniques, and methods for rationalizing denominators. It covers types of numbers such as real, rational, and irrational numbers, and offers various exercises for understanding these concepts. Additionally, it includes step-by-step examples and tips for simplifying expressions involving surds.

1. GCSE: Surds

2. Types of numbers
Real Numbers
Real numbers are any
possible decimal or
whole number.
Rational Numbers Irrational Numbers
are all numbers which
can be expressed as
some fraction involving
integers (whole
numbers), e.g.
1
4
, 3
1
2
, -7.
are real numbers which
are not rational.
!

3. Types of numbers
Activity: Copy out the
Venn diagram, and put
the following numbers
into the correct set.
3 0.7
π
.
1.3
√2 -1
3
4
√9 e
Edwin’s exact
height (in m)
Integers
Rational numbers
Real numbers
(Click the blue boxes above)

4. What is a surd?
Vote on whether you think the following are surds or not surds.
Therefore, can you think of a suitable definition for a surd?
A surd is a root of a number that cannot be simplified to a rational number.


Not a surd Surd
 
Not a surd Surd


Not a surd Surd
 
Not a surd Surd
?
3
7 

Not a surd Surd
2
9
5
1
4

5. Laws of Surds
𝑎 × 𝑏 = 𝒂𝒃
𝑎
𝑏
=
𝒂
𝒃
?
?
The only two things you need to know this topic…
Basic Examples:
4𝑥2 = 𝟒 𝒙𝟐 = 𝟐𝒙
1
9
=
𝟏
𝟑
?
?
3 × 2 = 𝟔 ?

6. Simplifying Surds
8 = 𝟒 𝟐 = 𝟐 𝟐
?
Could we somehow use 𝑎𝑏 = 𝑎 𝑏
to break the 8 up in a way that one of
the surds will simplify?
Bro Tip: Find the largest
square factor of the number,
and put that first.
?
27 = 𝟗 𝟑 = 𝟑 𝟑
32 = 𝟏𝟔 𝟐 = 𝟒 𝟐
2 50 = 𝟐 𝟐𝟓 𝟐 = 𝟏𝟎 𝟐
4 12 = 𝟒 𝟒 𝟑 = 𝟖 𝟑
?
?
?
?

7. Test Your Understanding
75 = 𝟐𝟓 𝟑 = 𝟓 𝟑
20 = 𝟒 𝟓 = 𝟐 𝟓
48 = 𝟏𝟔 𝟑 = 𝟒 𝟑
3 200 = 𝟑 𝟏𝟎𝟎 𝟐 = 𝟑𝟎 𝟐
5 45 = 𝟓 𝟗 𝟓 = 𝟏𝟓 𝟓
?
?
?
?
?

8. Multiplying Surds
3 × 5 = 𝟏𝟓
2 × 3 = 𝟐 𝟑
5 × 3 = 𝟑 𝟓
2 × 8 = 𝟏𝟔 = 𝟒
3 × 3 = 𝟗 = 𝟑
Bro Tip: Be very careful in
observing whether both
of the terms are surds or
just one is.
?
?
?
?
?
2 3 × 2 5 = 𝟒 𝟏𝟓
Bro Tip: Just multiply the
non-surdey things first,
then the surdey things.
?
3 2 × 3 2 = 𝟏𝟖?
18 × 4 2 = 𝟐𝟒?

9. Test Your Understanding
6 × 7 = 𝟔 𝟕
5 × 6 = 𝟑𝟎
2 × 2 = 𝟐 𝟐
5 3 × 4 3 = 𝟔𝟎
3 × 4 3 = 𝟏𝟐 𝟑
3 5
2
= 𝟒𝟓
5 8 × 2 2 = 𝟒𝟎
2 2 × 3 6 = 𝟔 𝟏𝟐 = 𝟔 𝟒 𝟑 = 𝟏𝟐 𝟑
?
?
?
?
?
?
?
?

10. Exercise 1
Simplify the following:
8 = 𝟐 𝟐
18 = 𝟑 𝟐
50 = 𝟓 𝟐
80 = 𝟒 𝟓
72 = 𝟔 𝟐
Simplify the following:
5 80 = 𝟐𝟎 𝟓
2 125 = 𝟏𝟎 𝟓
8 12 = 𝟏𝟔 𝟑
3 72 = 𝟏𝟖 𝟐
2 28 = 𝟒 𝟕
Simplify the following:
3 × 2 × 5 = 𝟑𝟎
27 × 3 = 𝟗
4 3 × 2 = 𝟖 𝟑
5 × 2 5 = 𝟏𝟎 𝟓
2 2 × 2 2 = 𝟖
7 3 × 2 5 = 𝟏𝟒 𝟏𝟓
6 3 × 2 3 = 𝟑𝟔
Simplify the following:
8 × 3 2 = 𝟏𝟐
27 × 2 3 = 𝟏𝟖
3 18 × 2 = 𝟏𝟖
2 12 × 3 3 = 𝟑𝟔
Express the following as a
single square root
(hint: do the steps of simplification
backwards!)
3 2 = 𝟗 𝟐 = 𝟏𝟖
2 5 = 𝟒 𝟓 = 𝟐𝟎
5 7 = 𝟏𝟕𝟓
4 3 = 𝟒𝟖
Express the following as a
single square root:
𝑎 𝑏 = 𝒂𝟐𝒃
2 𝑘 = 𝟒𝒌
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
1
2
3
4
5
6
a
b
c
d
e
a
b
c
d
e
a
b
c
d
e
f
g
a
b
c
d
a
b
c
d
a
b

11. Adding Surds
3 + 3 = 𝟐 𝟑
Think of it as “if I have one lot of 3 and I add another lot of
3, I have two lots of 3”.
It’s just how we collect like terms in algebra, e.g. 𝑥 + 𝑥 = 2𝑥
?
2 5 + 5 = 𝟑 𝟓
7 7 + 7 7 = 𝟏𝟒 𝟕
2 + 8 = 𝟐 + 𝟐 𝟐
= 𝟑 𝟐
3 12 + 27 = 𝟑 𝟒 𝟑 + 𝟗 𝟑
= 𝟔 𝟑 + 𝟑 𝟑
= 𝟗 𝟑
?
?
?
?

12. Test Your Understanding
3 + 3 + 3 = 𝟑 𝟑
8 + 18 = 𝟐 𝟐 + 𝟑 𝟐 = 𝟓 𝟐
2 5 + 2 20 = 𝟐 𝟓 + 𝟒 𝟓
= 𝟔 𝟓
3 48 + 12 = 𝟏𝟐 𝟑 + 𝟐 𝟑
= 𝟏𝟒 𝟑
?
?
?
?

13. Brackets and Surds
2 3 + 2 = 𝟑 𝟐 + 𝟐
2 + 1 2 − 1 = 𝟐 + 𝟐 − 𝟐 − 𝟏 = 𝟏
8 + 3 2 + 5 = 𝟏𝟔 + 𝟓 𝟖 + 𝟑 𝟐 + 𝟏𝟓
= 𝟒 + 𝟓 𝟒 𝟐 + 𝟑 𝟐 + 𝟏𝟓
= 𝟏𝟗 + 𝟏𝟎 𝟐 + 𝟑 𝟐
= 𝟏𝟗 + 𝟏𝟑 𝟐
5 − 2
2
= 𝟓 − 𝟐 𝟓 − 𝟐
= 𝟓 − 𝟐 𝟓 − 𝟐 𝟓 + 𝟒
= 𝟗 − 𝟒 𝟓
?
?
?
?

14. Test Your Understanding
5 2 + 3 = 𝟐 𝟓 + 𝟏𝟓
1 + 3 2 + 3 = 𝟓 + 𝟑 𝟑
8 − 1 2 + 3 = 𝟏 + 𝟓 𝟐
3 − 2 5
2
= 𝟐𝟗 − 𝟏𝟐 𝟓
3 + 3
1 + 3 3
𝐴𝑟𝑒𝑎 = 𝟔 + 𝟓 𝟑
?
?
?
?
?

16. Exercise 2
Simplify the following:
8 + 18 = 𝟓 𝟐
12 − 3 = 𝟑
20 + 45 = 𝟓 𝟓
3 + 12 + 27 = 𝟔 𝟑
300 − 48 = 𝟔 𝟑
2 50 + 3 32 = 𝟐𝟐 𝟐
Expand and simplify the following,
leaving your answers in the form
𝑎 + 𝑏 𝑐
3 2 + 3 = 𝟐 𝟑 + 𝟑
3 + 1 2 + 3 = 𝟓 + 𝟑 𝟑
5 − 1 2 + 5 = 𝟑 + 𝟓
7 + 1 2 − 2 7 = −𝟏𝟐
2 − 3
2
= 𝟕 − 𝟒 𝟑
Expand and simplify:
2 − 8 2 + 2 = −𝟐 𝟐
3 + 27 4 − 3 = 𝟑 + 𝟗 𝟑
2 2 + 5 4 + 18 = 𝟑𝟐 + 𝟐𝟑 𝟐
8 + 18 32 − 50 = −𝟏𝟎
2 + 1
2
− 2 − 1
2
= 𝟒 𝟐
3 + 2
2
− 3 − 2
2
= 𝟖 𝟑
Determine the area of :
2
+
3
3
5 + 3
5
−
1
4
+
3
5
6
−
5
5
𝑨 = 𝟐 𝟑 + 𝟑 𝑨 = 𝟏 + 𝟓 𝑨 = 𝟓 + 𝟓 𝟓
7 + 2
7 − 2
𝑃
𝑄
Find the length of 𝑃𝑄.
(Using Pythagoras)
𝑷𝑸 = 𝟐𝟐
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
? ? ?
?
1
a
b
c
d
e
f
2
a
b
c
d
e
3
a
b
c
d
e
f
4
a
b c
5

17. Here’s a surd. What could we multiply it by such that it’s no
longer an irrational number?
Rationalising The Denominator
5 × 5 = 5
? ?
In this fraction, the denominator is
irrational. ‘Rationalising the
denominator’ means making the
denominator a rational number.
What could we multiply this fraction by
to both rationalise the denominator, but
leave the value of the fraction
unchanged?
1
2
×
2
2
=
2
2
? ?
Bro Side Note: There’s two reasons
why we might want to do this:
1. For aesthetic reasons, it makes
more sense to say “half of root 2”
rather than “one root two-th of
1”. It’s nice to divide by
something whole!
2. It makes it easier for us to add
expressions involving surds.

18. 3
2
=
𝟑 𝟐
𝟐
6
3
=
𝟔 𝟑
𝟑
= 𝟐 𝟑
8
10
=
𝟖 𝟏𝟎
𝟏𝟎
=
𝟒 𝟏𝟎
𝟓
10
5
=
𝟏𝟎 𝟓
𝟓
= 𝟐 𝟓
7
7
=
𝟕 𝟕
𝟕
= 𝟕
More Examples
?
?
?
?
?
12
3
= 𝟒 𝟑
2
6
=
𝟔
𝟑
4 2
8
=
𝟏𝟔
𝟖
= 𝟐
?
?
?
Test Your Understanding:

19. FURTHER MATHS! :: More Complex Denominators
You’ve seen ‘rationalising a denominator’, the idea being that we don’t like to
divide things by an irrational number.
But what do we multiply the top and bottom by if we have a more complicated
denominator?
1
2 + 1
×
𝟐 − 𝟏
𝟐 − 𝟏
=
𝟐 − 𝟏
𝟏
= 𝟐 − 𝟏
? ?
We basically do the same but with the sign reversed (this is known as the ‘conjugate’).
That way, we obtain the difference of two squares. Since 𝑎 + 𝑏 𝑎 − 𝑏 = 𝑎2
− 𝑏2
,
any surds will be squared and thus we’ll end up with no surds in the denominator.

20. More Examples
3
6 − 2
×
6 + 2
6 + 2
=
3 6 + 6
2
You can explicitly expand out
6 − 2 6 + 2 in the
denominator, but remember
that 𝑎 − 𝑏 𝑎 + 𝑏 = 𝑎2
− 𝑏2
so we get 6 − 4 = 2
Just remember: ‘difference of
two squares’!
?
3 2 + 4
5 2 − 7
×
𝟓 𝟐 + 𝟕
𝟓 𝟐 + 𝟕
=
𝟑𝟎 + 𝟐𝟏 𝟐 + 𝟐𝟎 𝟐 + 𝟐𝟖
𝟏
= 𝟓𝟖 + 𝟒𝟏 𝟐
?
?
?
4
3 + 1
×
3 − 1
3 − 1
=
4 3 − 4
2
= 2 3 − 2
?
? ?

21. Test Your Understanding
AQA FM June 2013 Paper 1
Solve 𝑦 3 − 1 = 8
Give your answer in the form 𝑎 + 𝑏 3
where 𝑎 and 𝑏 are integers.
𝒚 =
𝟖
𝟑 − 𝟏
×
𝟑 + 𝟏
𝟑 + 𝟏
=
𝟖 𝟑 + 𝟖
𝟐
= 𝟒 + 𝟒 𝟑
Rationalise the denominator and
simplify
2 3 − 1
3 3 + 1
𝟐 𝟑 − 𝟏
𝟑 𝟑 + 𝟏
×
𝟑 𝟑 − 𝟏
𝟑 𝟑 − 𝟏
=
𝟏𝟖 − 𝟐 𝟑 − 𝟑 𝟑 + 𝟏
𝟐𝟕 − 𝟏
=
𝟏𝟗 − 𝟓 𝟑
𝟐𝟔
?
?
Rationalise the
denominator and simplify
4
5 − 2
𝟖 + 𝟒 𝟓
?

22. Exercise 3
Rationalise the denominator
and simplify the following:
1
5 + 2
= 𝟓 − 𝟐
3
3 − 1
=
𝟑 + 𝟑
𝟐
5 + 1
5 − 2
= 𝟕 + 𝟑 𝟓
2 3 − 1
3 3 + 4
= 𝟐 − 𝟑
5 5 − 2
2 5 − 3
= 𝟒 + 𝟓
Expand and simplify:
5 + 3 5 − 2 5 + 1 = 𝟒
Rationalise the denominator, giving
your answer in the form 𝑎 + 𝑏 3.
3 3 + 7
3 3 − 5
= 𝟑𝟏 + 𝟏𝟖 𝟑
Solve 𝑥 4 − 6 = 10 giving your
answer in the form 𝑎 + 𝑏 6.
𝑥 =
10
4 − 6
= 𝟒 + 𝟔
Solve 𝑦 1 + 2 − 2 = 3
𝑦 =
3 + 2
1 + 2
= 𝟐 𝟐 − 𝟏
Simplify:
𝑎 + 1 − 𝑎
𝑎 + 1 + 𝑎
= 𝟐𝒂 + 𝟏 − 𝟐 𝒂 𝒂 + 𝟏
?
?
?
?
?
?
?
?
?
1 2
3
4
5
a
b
c
d
e
?
6

23. A final super hard puzzle
Solve
4
9
5
27
=
𝑥
3
N
𝟒
𝟑𝟐
𝟓
𝟑𝟑
=
𝟑𝟐
𝟏
𝟒
𝟑𝟑
𝟏
𝟓
=
𝟑
𝟏
𝟐
𝟑
𝟑
𝟓
= 𝟑−
𝟏
𝟏𝟎
But
𝒙
𝟑 = 𝟑
𝟏
𝒙
∴
𝟏
𝒙
= −
𝟏
𝟏𝟎
→ 𝒙 = −𝟏𝟎
?