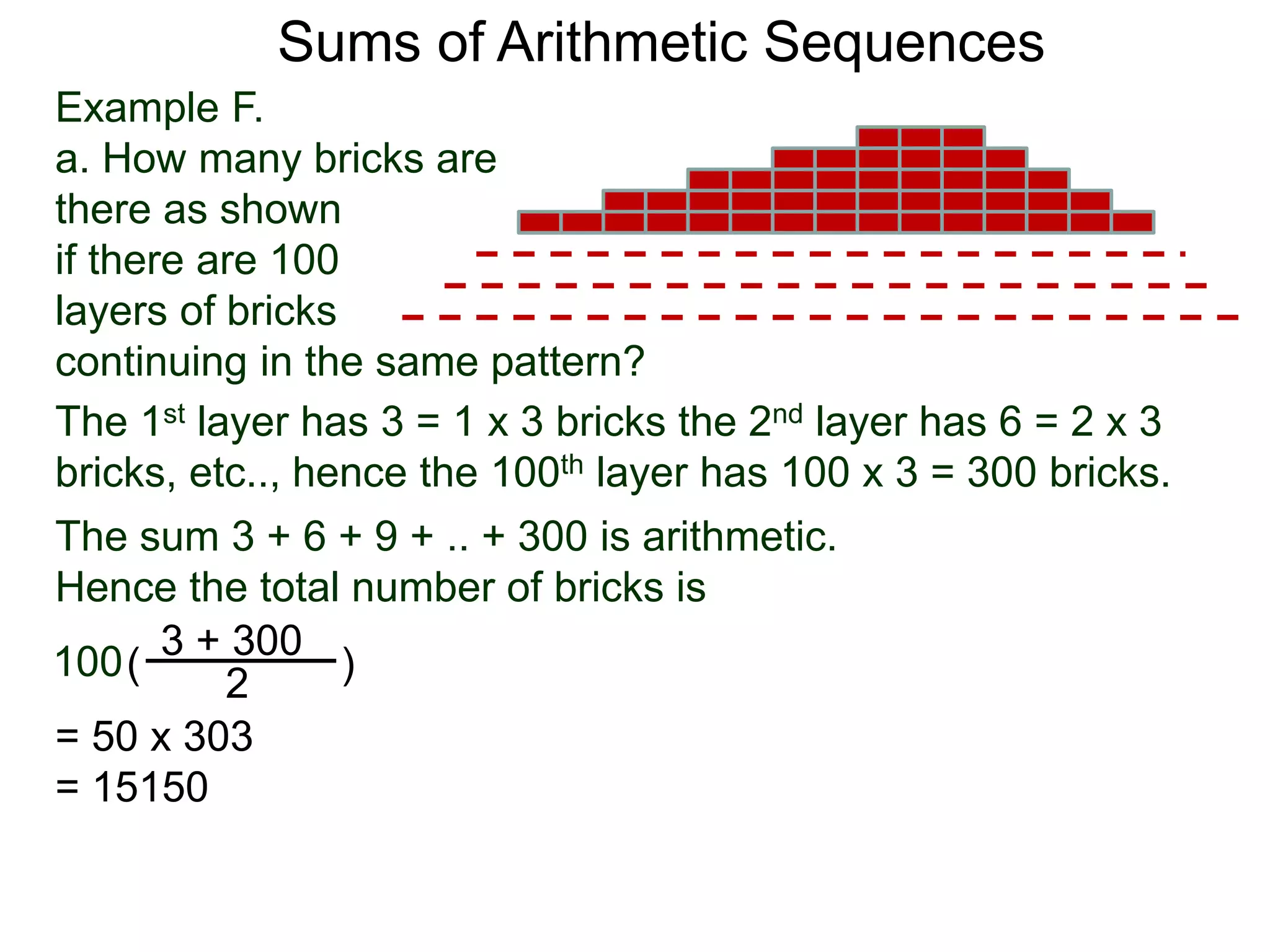
The document provides examples and explanations of arithmetic sequences. It defines an arithmetic sequence as a sequence where the difference between consecutive terms is constant. The general formula for an arithmetic sequence is given as an = d(n-1) + a1, where d is the common difference and a1 is the first term. Several examples are worked through applying this formula to find the specific formula for given sequences, as well as the nth term and sum of terms. The exercises consist of identifying arithmetic sequences based on given terms and using the general formula to find characteristics like the first term, difference, specific formula, and sum of terms.

1. Example B. Given the sequence 2, 5, 8, 11, …
a. Verify it is an arithmetic sequence.
It's arithmetic because 5 – 2 = 8 – 5 = 11 – 8 = … = 3 = d.
b. Find the (specific) formula that represents this sequence.
Plug a1 = 2 and d = 3, into the general formula
an = d(n – 1) + a1
we get
an = 3(n – 1) + 2
an = 3n – 3 + 2
an = 3n – 1 the specific formula.
c. Find a1000.
Set n = 1000 in the specific formula, we get
a1000 = 3(1000) – 1 = 2999.
Arithmetic Sequences
Use the arithmetic sequences general formula
an = d(n – 1) + a1 to find specific formulas for sequences.

2. Arithmetic Sequences
Find the first term a1 and the difference d to use the general
formula to find the specific formula,.
Set d = –4 in the general formula an = d(n – 1) + a1, we get
an = –4(n – 1) + a1.
Set n = 6 in this formula, we get
a6 = –4(6 – 1) + a1 = 5
–20 + a1 = 5
a1 = 25
To find the specific formula , set 25 for a1 in an = –4(n – 1) + a1
an = –4(n – 1) + 25
an = –4n + 4 + 25
an = –4n + 29
Example C. Given a1, a2 , a3 , …an arithmetic sequence with
d = -4 and a6 = 5, find a1, the specific formula and a1000.
To find a1000, set n = 1000 in the specific formula
a1000 = –4(1000) + 29 = –3971

3. Example D. Given that a1, a2 , a3 , …is an arithmetic sequence
with a3 = –3 and a9 = 39, find d, a1 and the specific formula.
Set n = 3 and n = 9 in the general arithmetic formula
an = d(n – 1) + a1, we get
a3 = d(3 – 1) + a1 = –3
2d + a1 = –3
Subtract these equations:
8d + a1 = 39
) 2d + a1 = -3
6d = 42
d = 7
Put d = 7 into 2d + a1 = -3,
2(7) + a1 = -3
14 + a1 = -3
a1 = – 17
Hence the specific formula is an = 7(n – 1) – 17
or an = 7n – 24.
Arithmetic Sequences
a9 = d(9 – 1) + a1 = 39
8d + a1 = 39

4. Given that a1, a2 , a3 , …an an arithmetic sequence, then
a1+ a2 + a3 + … + an = n
TailHead +
2( )
ana1 +
2( )= n
Example E.
a. Given the arithmetic sequence a1= 4, 7, 10, … , and
an = 67. What is n?
We need the specific formula. Find d = 7 – 4 = 3.
Therefore the specific formula is
an = 3(n – 1) + 4
an = 3n + 1.
Sums of Arithmetic Sequences
If an = 67 = 3n + 1, then 66 = 3n or 22 = n
n terms
b. Find the sum 4 + 7 + 10 +…+ 67
a1 = 4, and a22 = 67 with n = 22, so the sum
4 + 7 + 10 +…+ 67 = 22 = 11(71) = 781
4 + 67
2
( )11

5. Sums of Arithmetic Sequences
Example F.
a. How many bricks are
there as shown
if there are 100
layers of bricks
continuing in the same pattern?
The 1st layer has 3 = 1 x 3 bricks the 2nd layer has 6 = 2 x 3
bricks, etc.., hence the 100th layer has 100 x 3 = 300 bricks.
3 + 300
2( )
The sum 3 + 6 + 9 + .. + 300 is arithmetic.
Hence the total number of bricks is
100
= 50 x 303
= 15150

6. Arithmetic Sequences
2. –2, –5, –8, –11,..1. 2, 5, 8, 11,..
4. –12, –5, 2, 9,..3. 6, 2, –2, –6,..
6. 23, 37, 51,..5. –12, –25, –38,..
8. –17, .., a7 = 13, ..7. 18, .., a4 = –12, ..
10. a12 = 43, d = 59. a4 = –12, d = 6
12. a42 = 125, d = –511. a8 = 21.3, d = –0.4
14. a22 = 25, a42 = 12513. a6 = 21, a17 = 54
16. a17 = 25, a42 = 12515. a3 = –4, a17 = –11,
Exercise A. For each arithmetic sequence below
a. find the first term a1 and the difference d
b. find a specific formula for an and a100
c. find the sum  ann=1
100

7. B. For each sum below, find the specific formula of
the terms, write the sum in the  notation,
then find the sum.
1. – 4 – 1 + 2 +…+ 302
Sum of Arithmetic Sequences
2. – 4 – 9 – 14 … – 1999
3. 27 + 24 + 21 … – 1992
4. 3 + 9 + 15 … + 111,111,111
5. We see that it’s possible to add infinitely many
numbers and obtain a finite sum.
For example ½ + ¼ + 1/8 + 1/16... = 1.
Give a reason why the sum of infinitely many terms
of an arithmetic sequence is never finite,
except for 0 + 0 + 0 + 0..= 0.

8. Arithmetic Sequences
1. a1 = 2
d = 3
an = 3n – 1
a100 = 299
 an = 15 050
(Answers to the odd problems) Exercise A.
n=1
100
3. a1 = 6
d = – 4
an = – 4n + 10
a100 = – 390
 an = – 19 200n=1
100
5. a1 = – 12
d = –13
an = – 13n + 1
a100 = – 129
 an = – 65 550n=1
100
7. a1 = 18
d = – 10
an = – 10n +28
a100 = – 972
 an = – 47 700n=1
100
9. a1 = –30
d = 6
an = 6n – 36
a100 = 564
 an = 26 700n=1
100
11. a1 = 24.1
d = –0.4
an = –0.4n + 24.5
a100 = –15.5
 an = 430n=1
100

9. Arithmetic Sequences
13. a1 = 6
d = 3
an = 3n + 3
a100 = 303
 an = 15 450n=1
100
15. a1 = –3
d = – 0.5
an = – 0.5n – 2.5
a100 = –52.5
 an = –2 775n=1
100
Exercise B.
1. – 4 – 1 + 2 +…+ 302 =  3n – 7 = 15 347
3. 27 + 24 + 21 … – 1992 =  –3n + 30 = –662 205
n=1
103
n=1
674