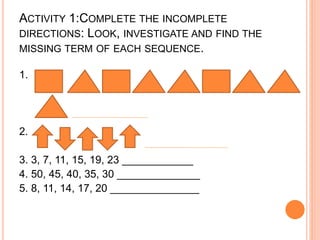
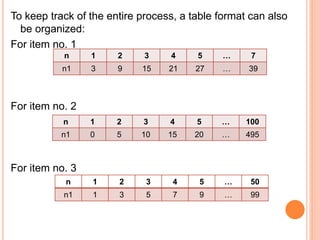
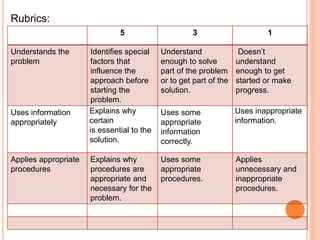
This document discusses arithmetic sequences. It begins by defining an arithmetic sequence as a sequence of numbers where the difference between consecutive terms is constant. It provides the formula an = a1 + (n-1)d to calculate the nth term, where an is the nth term, a1 is the first term, d is the common difference. Several examples are worked out applying this formula. Real-life examples of arithmetic sequences are discussed, like rows of seats in a stadium increasing by a constant amount. Students are assigned problems evaluating arithmetic sequences and finding specific terms, as well as researching other real-world applications of arithmetic sequences.

2. ARITHMETIC
SEQUENCE

3. OBJECTIVES
1. Learn and define arithmetic sequence,
2. Illustrate an arithmetic sequence,
3. realize the importance and application of
arithmetic sequence in real life setting.

4. ACTIVITY 1:COMPLETE THE INCOMPLETE
DIRECTIONS: LOOK, INVESTIGATE AND FIND THE
MISSING TERM OF EACH SEQUENCE.
1.
2.
3. 3, 7, 11, 15, 19, 23 ____________
4. 50, 45, 40, 35, 30 ______________
5. 8, 11, 14, 17, 20 _______________

5. UNLOCKING OF DIFFICULTIES
 Arithmetic sequence or arithmetic progression
-- is a sequence of numbers such that the difference
from any succeeding term to its preceding term
remains constant throughout the sequence. The
constant difference is called common difference of
the arithmetic progression.
● Formula: an = a1 + (n – 1)d where;
an = the nth term in the sequence
a1 = the first term in the sequence
d = the common difference between terms

6. Johann Carl Friedrich Gauss
-- is the father of Arithmetic Progression.
He found it when he was in school and his teacher asked to
sum the integers from 1 – 100.

7. ILLUSTRATIVE EXAMPLES
1. Find the 7th term of the arithmetic sequence 3, 9,
15, 21, 27, …
2. What is the 100th term of the sequence 0, 5, 10, 15,
…?
3. What is the 50th term of the sequence 1, 3, 5, 7, 9,
…?
2
3

8. 1. solutions:
Let us first find the common difference of the given sequence
we have; (9 – 3 = 6)
an = a1 + (n – 1)d
a7 = 3 + ( 7 – 1) 6
a7 = 3 + (6)6
a7 = 3 + 36
a7 = 39

9. 2. solutions:
an = a1 + (n – 1)d
a100 = 0 + (100 – 1) 5
a100 = 0 + (99)5
a100 = 0 + 495
a100 = 495

10. 3. solutions:
3 -1 = 2
d = 2
a50 = 1 + (50 – 1)2
a50 = 1 + (49)2
a50 = 1 + 98
a50 = 99
an = a1 + (n – 1)d

11. To keep track of the entire process, a table format can also
be organized:
For item no. 1
For item no. 2
For item no. 3
n 1 2 3 4 5 … 7
n1 3 9 15 21 27 … 39
n 1 2 3 4 5 … 100
n1 0 5 10 15 20 … 495
n 1 2 3 4 5 … 50
n1 1 3 5 7 9 … 99

12. ENRICHMENT ACTIVITY: ARITHMETIC SEQUENCE IN
REAL LIFE
DIRECTIONS: IDENTIFY WHICH AMONG THE IMAGES
CLEARLY DEPICTS AN ARITHMETIC SEQUENCE AND
WHICH DO NOT.
1
2

13. 3
4
5

14. 6

15. 1. Arithmetic Sequence 1, 2, 3, 4, 5, 6

16. 2. Arithmetic Sequence (nearer seats in a stadium or arena
are less than those that are further, each row contains
different numbers of seats in an increasing order from
nearer to further seats).

17. 3. Arithmetic Sequence with common difference of 3.

18. 4. A sequence but does not clearly depicts an arithmetic
sequence.

19. 5. An Arithmetic Sequence with 0 as common difference.

20. 6. Arithmetic Sequence 1, 2, 3, 4

21. EVALUATION
Directions: In a one whole sheet of paper answer the
following questions comprehensively and show your
solutions.
1. Given the arithmetic sequence 2, 4, 6, 8, 10, … find a50.
a. 100 b. 108 c. 115 d. 105
2 – 4 . Find the a11, a23, and a30 of the arithmetic sequence
1, 5, 9, 13, 17, …
a. a11 = 50, a23 = 90, a30 = 118
b. a11 = 53, a23 = 95, a30 = 120
c. a11 = 49, a23 = 89, a30 = 117
d. a11 = 56, a23 = 92, a30 = 120
5. 295 is what term of the arithmetic sequence 10, 25, 40,
…?

22. a. a20 b. a25 c. a23 d. a28
6. Given 2, 125, 248, 371. Find the d.
a. d = 125 b. d = 123 c. d = 130 d. d = 126
7. Find the 250th term in the sequence 37, 50, 63, 76,…
a. a250 = 3,270 c. a250 = 3,277
b. A250 = 3,271 d. a250 = 3,274
8. What should be the value of x so that x + 2, 3x – 2, 7x – 12
will form an arithmetic sequence?
a. x = 5 b. x = 3 c. x = 2 d. x = 8
9. There are 115 passengers in the first carriage of a train,
130 passengers in the second carriage and 145 in the
third carriage and so on. How many passengers will there
be in the 8th carriage?
a. a8 = 220passengers c. a8 = 230passengers
b. a8 = 225passengers d. a8 = 235passengers

23. 10. A racing car travels 750 meters in a minute. If the car
begins racing at exactly 8:00am, what time will he reach
the finish line if the distance covered by one lap is 10
kilometers and the car needs to complete 3 lapses?
a. 9:00am b. 8:30am c. 8:40am d. 9:15am

24. ASSIGNMENT
 Directions: Research on other examples of
applications of arithmetic sequence in real – life
setting.
Paste the examples in a piece of long bond paper.
Elaborately explain why such examples belong
specifically to an arithmetic sequence.

25. Rubrics:
5 3 1
Understands the
problem
Identifies special
factors that
influence the
approach before
starting the
problem.
Understand
enough to solve
part of the problem
or to get part of the
solution.
Doesn’t
understand
enough to get
started or make
progress.
Uses information
appropriately
Explains why
certain
is essential to the
solution.
Uses some
appropriate
information
correctly.
Uses inappropriate
information.
Applies appropriate
procedures
Explains why
procedures are
appropriate and
necessary for the
problem.
Uses some
appropriate
procedures.
Applies
unnecessary and
inappropriate
procedures.

26. Uses
representations
Uses a
representation
that is appropriate
and fits to its
mathematical
precision.
Uses a
representation
that gives some
important
information about
the problem.
Uses a
representation
that gives little or
no significant
information about
the problem.
Answers the
problem
Correct solutions
of the problem
and made a
general rule about
the solution or
extend the
solution to a more
detailed and brief
generalization.
Partially correct
solution and with
copying and
computational
error, and answer
are labeled
incorrectly.
Incorrect solution
or no answer at all
based on
inappropriate
method.