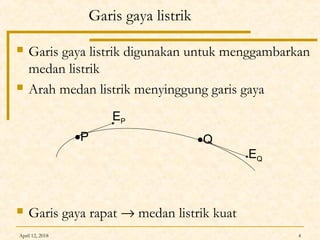
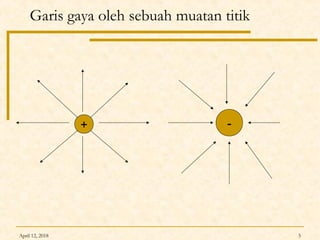
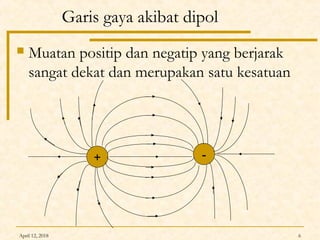
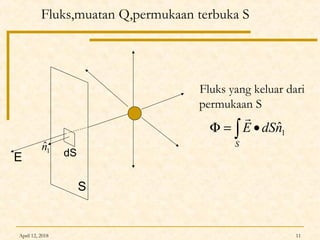
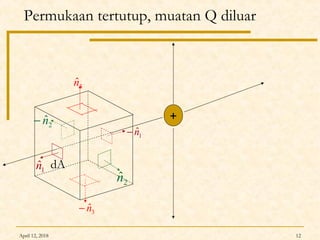
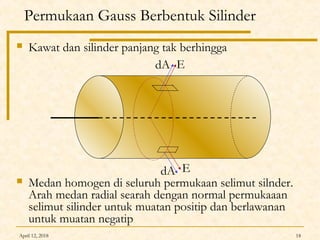
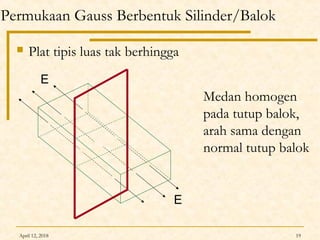
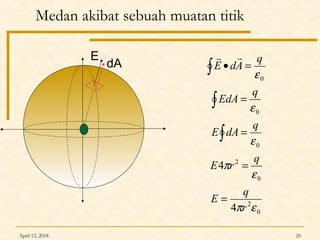
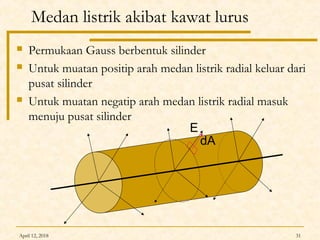
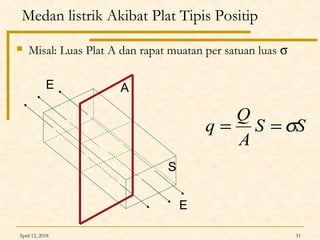
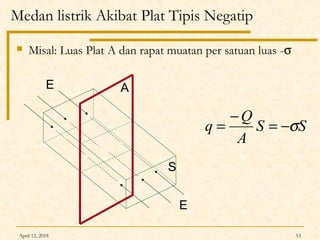
Dokumen ini membahas Hukum Gauss dalam fisika, termasuk konsep garis gaya listrik, fluks listrik, dan penerapan teorema Gauss untuk menghitung medan listrik dari berbagai konfigurasi muatan. Diterangkan pula tentang perbedaan antara konduktor dan isolator dalam hal distribusi muatan dan medan listrik. Terdapat juga contoh soal dan perhitungan terkait hukum Gauss pada muatan titik, bola, dan silinder.

1. April 12, 2018 1

2. April 12, 2018 2
Hukum Gauss
Garis Gaya Listrik
Konsep fluks
Pengertian Hukum Gauss
Penggunaan Hukum Gauss
Medan oleh muatan titik
Medan oleh kawat panjang tak berhingga
Medan listrik oleh plat luas tak berhingga
Medan listrik oleh bola isolator dan konduktor
Medan listrik oleh silinder isolator dan konduktor
Muatan induksi

3. SASARAN PEMBELAJARAN
 Mahasiswa mampu menghitung besar medan
listrik menggunakan hukum Gauss
April 12, 2018 3

4. April 12, 2018 4
Garis gaya listrik
 Garis gaya listrik digunakan untuk menggambarkan
medan listrik
 Arah medan listrik menyinggung garis gaya
 Garis gaya rapat → medan listrik kuat
•P
EP
•Q
EQ

5. April 12, 2018 5
Garis gaya oleh sebuah muatan titik
+ -

6. April 12, 2018 6
Garis gaya akibat dipol
 Muatan positip dan negatip yang berjarak
sangat dekat dan merupakan satu kesatuan
+ -

7. April 12, 2018 7
Fluks Listrik
 Definisi: banyaknya garis gaya listrik yang menembus suatu
permukaan
 Untuk permukaan dA yang tegak lurus dengan arah medan,
jumlah garis gaya yang menembus permukaan itu adalah
 Total garis gaya yang
menembus permukaan A
EdAd =Φ
dA
EA
EAdAE
EdAd
A
AA
==
=Φ=Φ
∫
∫∫

8. April 12, 2018 8
Fluks untuk sembarang permukaan
 Untuk sembarang permukaan dA dengan arah
tidak tegak lurus medan
AdEd

•=ΦdA
∫
∫
•=
Φ=Φ
S
S
AdE
d

Fluks total untuk
permukaan SE
S

9. April 12, 2018 9
Contoh soal
 Sebuah medan listrik dinyatakan dalam persamaan .
Tentukan fluks yang menembus permukaan
a. b.
c. d.
d. e.
 Solusi
Karena medan homogen di seluruh permukaan yang
ditinjau, maka fluks dapat dituliskan dalam bentuk
jiE ˆ4ˆ2 +=

iS ˆ10=
 jS ˆ10=

kS ˆ10=

kS ˆ10−=

jS ˆ10−=

iS ˆ10−=

SEAdE
S

•→•∫

10. April 12, 2018 10
Solusi contoh soal
a.
b.
c.
d.
e.
f.
0ˆ10)ˆ4ˆ2( =•+=•=Φ kjiAE

0ˆ10)ˆ4ˆ2( =−•+=•=Φ kjiAE

40ˆ10)ˆ4ˆ2( =•+=•=Φ jjiAE

40ˆ10)ˆ4ˆ2( −=−•+=•=Φ jjiAE

20ˆ10)ˆ4ˆ2( =•+=•=Φ ijiAE

20ˆ10)ˆ4ˆ2( −=−•+=•=Φ ijiAE


11. April 12, 2018 11
Fluks,muatan Q,permukaan terbuka S
Fluks yang keluar dari
permukaan S
∫ •=Φ
S
ndSE 1
ˆ

1
ˆn
S
dSE

12. April 12, 2018 12
Permukaan tertutup, muatan Q diluar
+
1
ˆn dA
1
ˆn−
2
ˆn
2
ˆn−
3
ˆn
3
ˆn−

13. April 12, 2018 13
Perhitungan fluks Q diluar permukaan
 Perhatikan arah normal permukaan dan arah medan listrik
 Fluks total pada kubus mempunyai nilai:
0
0000
)ˆ(ˆ
)ˆ(ˆ
)ˆ(ˆ
11
33
22
11
=
−+−+Φ−Φ=
−•+•
+−•+•
+−•+•=
•=Φ
∫∫
∫∫
∫∫
∫
SS
SS
SS
S
ndAEndAE
ndAEndAE
ndAEndAE
AdE





14. April 12, 2018 14
Permukaan tertutup, Q di dalam
2
ˆn
2
ˆn−
1
ˆn dA
1
ˆn−
3
ˆn
3
ˆn−

15. April 12, 2018 15
Perhitungan fluks Q di dalam
 Perhatikan arah normal permukaan dan arah medan listrik
 Fluks total pada kubus mempunyai nilai:
0
)ˆ(ˆ
)ˆ(ˆ
)ˆ(ˆ
332211
33
22
11
≠
Φ+Φ+Φ+Φ+Φ+Φ=
−•+•
+−•+•
+−•+•=
•=Φ
∫∫
∫∫
∫∫
∫
SS
SS
SS
S
ndAEndAE
ndAEndAE
ndAEndAE
AdE





16. April 12, 2018 16
Hukum Gauss
 Besar fluks atau garis gaya listrik yang keluar dari
suatu permukaan tertutup sebanding muatan yang
dilingkupi oleh luasan tertutup tersebut
 Prinsip untuk menggunakan teorema Gauss
dengan mudah
 Pilih permukaan yang medan listrik di permukaan
tersebut homogen
 Tentukan muatan yang dilingkupi permukaan tersebut
 Tentukan arah medan terhadap arah normal
permukaan.
∫ =•
0ε
q
SdE


17. April 12, 2018 17
Permukaan Gauss Berbentuk Bola
 Untuk muatan titik dan bola
dAE Medan dipermukaan
bola homogen.
Untuk muatan positip:
arah medan radial,
searah dengan normal
permukaan bola
Untuk muatan negatip
arah medan berlawana
dengan arah normal
permukaan

18. April 12, 2018 18
Permukaan Gauss Berbentuk Silinder
 Kawat dan silinder panjang tak berhingga
 Medan homogen di seluruh permukaan selimut silnder.
Arah medan radial searah dengan normal permukaaan
selimut silinder untuk muatan positip dan berlawanan
untuk muatan negatip
dA E
EdA

19. April 12, 2018 19
Permukaan Gauss Berbentuk Silinder/Balok
 Plat tipis luas tak berhingga
E
E
Medan homogen
pada tutup balok,
arah sama dengan
normal tutup balok

20. April 12, 2018 20
Medan akibat sebuah muatan titik
dA
E
0
2
0
2
0
0
0
4
4
επ
ε
π
ε
ε
ε
r
q
E
q
rE
q
dAE
q
EdA
q
AdE
=
=
=
=
=•
∫
∫
∫


21. April 12, 2018 21
Konduktor dan Non-Konduktor (Isolator)
 Di dalam konduktor, muatan bebas bergerak
 Jika diberi muatan tambahan dari luar → muncul
medan listrik → muatan bergerak menghasilkan
arus internal → terjadi distribusi ulang muatan
tambahan dari luar hingga tercapai keseimbangan
elektrostatis → medan listrik di dalam konduktor
menjadi nol → menurut hukum Gauss berarti
muatan di dalam konduktor nol, muatan
tambahan dari luar tersebar di permukaan
konduktor

22. April 12, 2018 22
 Waktu yang diperlukan untuk mencapai
keseimbangan elektrostatis pada koduktor sangat
cepat
 Medan listrik di dalam konduktor boleh dianggap
selalu nol dan muatan dari luar selalu ada di
permukaan konduktor
 Di dalam isolator muatan tidak bebas bergerak
 Muatan tambahan dari luar akan terdistribusi
merata dalam isolator

23. April 12, 2018 23
Bola konduktor pejal positip
 Tinjau suatu bola konduktor pejal dengan jari-jari
R dan muatan Q
dA
E
•Muatan hanya tersebar
di permukaan bola saja
•Medan listrik di dalam
bola (r<R) nol

24. April 12, 2018 24
Medan listrik di luar bola konduktor
 Untuk r>R, total muatan yang dilingkupi
permukaan Gauss adalah Q
 Hukum Gauss untuk kasus bola konduktor
pejal:
 Dengan r>R
2
00
2
00
4
4
r
Q
E
Q
rE
Q
dSE
q
SdE
πεε
π
εε
=→=
=→=• ∫∫


25. April 12, 2018 25
Bola isolator pejal
 Isolator: muatan tersebar merata di seluruh
volum isolator
 Di dalam bola
Q
R
r
Q
R
r
q 3
3
3
3
4
3
3
4
==
π
π
r
Q
R
r
E
Q
R
r
rE
Q
R
r
SdE
q
SdE
3
0
3
0
3
2
3
0
3
0
4
4
πε
ε
π
ε
ε
=
=
=
=•
∫
∫


R

26. April 12, 2018 26
Bola isolator pejal (2)
 Medan di luar
2
0
0
2
0
0
4
4
r
Q
E
Q
rE
Q
dSE
Q
SdE
πε
ε
π
ε
ε
=
=
=
=•
∫
∫

Rr
q=Q

27. April 12, 2018 27
Medan listrik pada bola isolator berongga
Q
RR
Rr
q 3
13
43
23
4
3
13
43
3
4
ππ
ππ
−
−
=
R1
R2
r
2
0
3
1
3
2
3
1
3
0
3
13
43
23
4
3
13
43
3
4
0
4
1
r
Q
RR
Rr
E
Q
RR
Rr
dSE
q
SdE
πε
εππ
ππ
ε
−
−
=
−
−
=
=•
∫
∫


28. April 12, 2018 28
Bola bermuatan negatip
 Pada prinsipnya sama dengan bola bermuatan positip
hanya arah medan listriknya masuk menuju pusat bola
E
dA
2
0
0
2
0
0
4
4
180cos
r
Q
E
Q
rE
Q
EdS
Q
SdE
πε
ε
π
ε
ε
=
=
−
=
−
=•
∫
∫


29. April 12, 2018 29
Dua bola, jenis muatan beda
 Sebuah bola tipis jari-jari a bermuatan 2Q. Di
dalam bola tipis diletakkan bola pejal konduktor
berjari-jari b dan bermuatan –3Q.
Medan listrik untuk daerah r<a
ditentukan dengan cara
yang sama dengan contoh
mencari medan pada bola
pejal
ab

30. April 12, 2018 30
2
00
2
00
4
4
180cos
r
Q
E
Q
rE
Q
EdS
q
SdE
πεε
π
εε
=→=
−
=→=• ∫∫

Medan untuk r>a
•Dibuat permukaan Gauss berbentuk bola dengan jari-
jari r>a
•Total muatan yang dilingkupi permukaan Gauss:
q=2Q+(-3Q)=-Q
•Medan akibat muatan -Q

31. April 12, 2018 31
Medan listrik akibat kawat lurus
 Permukaan Gauss berbentuk silinder
 Untuk muatan positip arah medan listrik radial keluar dari
pusat silinder
 Untuk muatan negatip arah medan listrik radial masuk
menuju pusat silinder
dA
E

32. April 12, 2018 32
Medan akibat kawat tak berhingga
rlE
EdSEdSEdS
SdESdESdESdE
tutupungsetutup
tutupungsetutup
π2
90cos0cos90cos lub
lub
=
++=
•+•+•=•
∫∫∫
∫∫∫∫

Fluks medan listrik yang menembus permukaan silinder
Jika panjang kawat L, muatan total Q, maka muatan yang
dilingkupi oleh silinder:
ll
L
Q
q λ==

33. April 12, 2018 33
Hukum Gauss untuk kawat sangat panjang
 Penentuan medan listrik
r
rL
Q
E
l
L
Q
rlE
q
SdE
0
0
0
0
2
2
2
πε
λ
πε
ε
π
ε
=
=
=
=•∫


34. April 12, 2018 34
Contoh soal untuk kawat panjang (1)
 Tentukan medan listrik dan gambarkan arahnya pada
titik A dan B yang berjarak 20 cm dari kawat dengan
rapat muatan λ=10 mC/m seperti pada gambar.
 Solusi :
ππππ
λ 025,0
4
1,0
)2,0(2
10.10
2
3
====
−
r
E
•A
•B
N/C

35. April 12, 2018 35
Contoh soal untuk kawat panjang (2)
 Tentukan medan listrik dan gambarkan arahnya pada
titik A dan B yang berjarak 20 cm dari kawat dengan
rapat muatan λ=-10 mC/m seperti pada gambar.
 Solusi :
ππππ
λ 025,0
4
1,0
)2,0(2
10.10
2
3
====
−
r
E
•A
•B
N/C

36. April 12, 2018 36
Medan listrik karena dua kawat sejajar
 Dua buah kawat pajang tak berhingga diberi muatan
masing-masing dengan rapat muatan λ dan -2 λ. Jarak
kedua kawat a. Tentukan medan listrik pada titik P yang
berjarak b dari kawat -2Q.
λλ EEEtotal

+= −2
λ -2λ
ba P
E-2λ
Eλ
)(2
2
)(2
2
00
2
bab
EEEtotal
+
−=
−= −
πε
λ
πε
λ
λλ

37. April 12, 2018 37
Medan listrik akibat silinder
 Misalkan silinder konduktor berjari-jari R ,
panjangnya L, dan bermuatan Q.
 Permukaan Gauss berbentuk silinder dengan jari-
jari r dan panjang L seperti kawat panjang tak
berhingga
 Untuk muatan positip, medan listrik berarah radial
meninggalkan sumbu pusat silinder
 Untuk muatan negatip, medan listrik berarah
radial menuju sumbu pusat silinder

38. April 12, 2018 38
Permukaan Gauss pada silinder
 Muatan positip
E
dA ∫
∫
∫
=
=
=•
0
0
0
0cos
ε
ε
ε
q
dAE
q
EdA
q
AdE


39. April 12, 2018 39
Permukaan Gauss pada silinder
 Muatan negatip
E
dA ∫
∫
∫
=
−
=
=•
0
0
0
180cos
ε
ε
ε
q
dAE
q
EdA
q
AdE


40. April 12, 2018 40
Medan listrik pada silinder konduktor pejal
 Di dalam konduktor
 Muatan yang dilingkupi permukaan Gauss =0 karena
pada konduktor muatan hanya tersebar di permukaan
konduktor saja. Dengan demikian, medan listrik di
dalam konduktor E=0

41. April 12, 2018 41
Medan listrik akibat silinder konduktor pejal
 Di luar konduktor
 Muatan yang dilingkupi permukaan Gauss
Qq =

42. April 12, 2018 42
Medan akibat silinder konduktor
 Medan listrik di luar silinder konduktor
Lr
Q
E
Q
rLE
Q
dAE
q
AdE
0
0
0
0
2
2
πε
ε
π
ε
ε
=
=
=
=•
∫
∫


43. April 12, 2018 43
Medan listrik pada silinder isolator pejal
 Di dalam isolator
 Muatan yang dilingkupi permukaan Gauss
Q
R
r
Q
LR
Lr
q 2
2
2
2
==
π
π

44. April 12, 2018 44
Silinder isolator pejal
 Medan listrik di dalam isolator (r<R)
Q
LR
r
E
Q
R
r
rLE
Q
R
r
dAE
q
AdE
2
0
2
0
2
2
0
2
0
2
2
πε
ε
π
ε
ε
=
=
=
=•
∫
∫


45. April 12, 2018 45
Silinder isolator pejal (2)
 Medan di luar silinder (r>R)
Lr
Q
E
Q
rLE
Q
dAE
q
AdE
0
0
0
0
2
2
πε
ε
π
ε
ε
=
=
=
=•
∫
∫


46. April 12, 2018 46
Silinder Isolator Berongga
 Jari-jari dalam silinder a, jari-jari luar b, muatan Q,
dan panjang silinder L
 Untuk r<a, E=0, karena q=0

47. April 12, 2018 47
Silinder isolator berongga (2)
 Untuk r>b, semua muatan terlingkupi oleh permukaan
Gauss ( q=Q), sehingga medan di luar silinder adalah:
 Untuk a<r<b, dibuat permukaan Gauss berbentuk
silinder dengan jari-jari a<r<b dan panjang L
 Muatan yang dilingkupi
Q
ab
ar
LaLr
LaLb
Q
Vq Gausssilinder
)(
)(
22
22
22
22
−
−
=−
−
== ππ
ππ
ρ
Lr
Q
E
02πε
=

48. April 12, 2018 48
Bola isolator berongga
Lrab
Qar
E
ab
Qar
rLE
ab
Qar
dAE
q
AdE
)(2
)(
)(
)(
2
)(
)(
22
0
22
22
0
22
22
0
22
0
−
−
=
−
−
=
−
−
=
=•
∫
∫
πε
ε
π
ε
ε

Medan listrik untuk a<r<b

49. April 12, 2018 49
Dua silinder dengan muatan berbeda
 Silinder pejal isolator berjari-jari a, panjang c, dan
bermuatan 3Q berada dalam suatu silinder berongga
yang jari-jari dalamnya b, jari-jari luarnya d, panjangnya c,
dan bermuatan –Q.
 Di dalam isolator (r<a)
Q
a
r
Q
ca
cr
q 33 2
2
2
2
==
π
π
0
22
0
2
0
22
2
33
2
3)/(
επε
π
ε ca
Qr
E
a
Qr
rcE
Qar
SdE =→=→=•∫


50. April 12, 2018 50
000 2
22
2
2
επε
π
ε rc
Q
E
Q
rcE
Q
SdE =→=→=•∫

Di antara isolator dan konduktor (a<r<b)
Di dalam konduktor (b<r<d): E=0
Di luar kondukto (r>d)
000 2
33
2
3
επε
π
ε rc
Q
E
Q
rcE
Q
SdE =→=→=•∫


51. April 12, 2018 51
Medan listrik Akibat Plat Tipis Positip
 Misal: Luas Plat A dan rapat muatan per satuan luas σ
E
E
SS
A
Q
q σ==
A
S

52. April 12, 2018 52
Perhitungan medan listrik akibat plat tipis (1)
0
0
0
2
2
ε
σ
ε
σ
ε
=
=
=•∫
E
S
SE
q
AdE

ES
ESES
SdESdESdESdE tutupungsetutup
2
0
lub
=
++=
•+•+•=• ∫∫∫∫


53. April 12, 2018 53
Medan listrik Akibat Plat Tipis Negatip
 Misal: Luas Plat A dan rapat muatan per satuan luas -σ
E
E
SS
A
Q
q σ−=
−
=
A
S

54. April 12, 2018 54
Perhitungan medan listrik akibat plat tipis(2)
0
0
0
2
)2(
ε
σ
ε
σ
ε
=
−
=−
=•∫
E
S
SE
q
AdE

ES
ESES
SdESdESdESdE tutupungsetutup
2
0
lub
−=
−+−=
•+•+•=• ∫∫∫∫


55. April 12, 2018 55
Medan listrik akibat dua plat tipis
 Dua plat tipis luas tak berhingga masing-masing
mempunyai rapat muatan σ dan - σ. Medan listrik di
sekitar plat tersebut dapat dianalisis seperti gambar di
bawah ini
02ε
σ
σσ == −EE
σ -σ
E1 E2 E3
0)()ˆ(
)()ˆ(
0)()ˆ(
3
0
2
1
=−+=
=+=
=+−=
−
−
−
iEiEE
iEiEE
iEiEE
σσ
σσ
σσ
ε
σ




56. April 12, 2018 56
Medan akibat 3 plat tipis
 Tiga buah plat tipis masing-masing bermuatan σ, -σ, dan
2σ. Medan di sekitar plat bisa dicari dengan cara berikut
σ - σ 2 σ
x=2 x=4 x=7
σσσ 2EEEEtotal

++= −

57. April 12, 2018 57
Medan listrik akibat 3 plat tipis (2)
i
iii
iEiEiExE
ˆ
2
ˆ
2
2ˆ
2
ˆ
2
)ˆ()ˆ()ˆ()2(
0
000
2
ε
σ
ε
σ
ε
σ
ε
σ
σσσ
=
++−=
++−=< −

i
iii
iEiEiExE
ˆ
2
4
ˆ
2
2ˆ
2
ˆ
2
)ˆ()ˆ()ˆ()42(
0
000
2
ε
σ
ε
σ
ε
σ
ε
σ
σσσ
=
++=
++=<< −

i
iii
iEiEiExE
ˆ
2
2
ˆ
2
2ˆ
2
ˆ
2
)ˆ()ˆ()ˆ()74(
0
000
2
ε
σ
ε
σ
ε
σ
ε
σ
σσσ
−=
−−=
+−+=<< −

i
iii
iEiEiExE
ˆ
2
2
ˆ
2
2ˆ
2
ˆ
2
)ˆ()ˆ()ˆ()7(
0
000
2
ε
σ
ε
σ
ε
σ
ε
σ
σσσ
=
+−=
+−+=> −


58. April 12, 2018 58
Muatan induksi
 Muatan muncul akibat pengaruh medan listrik eksternal
 Di dalam logam tipis: E+E´=0
0
'
2 00
=−
ε
σ
ε
σ
ii
σ
logam netral
- +
-
-
-
+
+
+
E E E’
2
'
σ
σ =
-σ´ σ´
-
+

59. April 12, 2018 59
Logam Ditanahkan
 Muatan muncul akibat pengaruh medan listrik eksternal
σ
logam netral
-
-
-
-
E E
E’
-σ´
-
+
+
+
+
σ´
+
Medan di dalam logam tetap nol, tapi komposisi muatan
jadi berubah. Diperoleh σ’=σ

60. April 12, 2018 60
 Di dalam logam (daerah 3) medan listrik total nol
 Karena ditanahkan, daerah 4 medan listriknya juga nol
σσ −='
0´
3 =+= EEE
