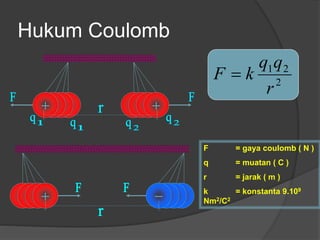
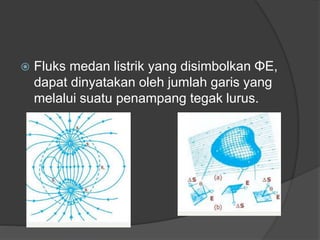
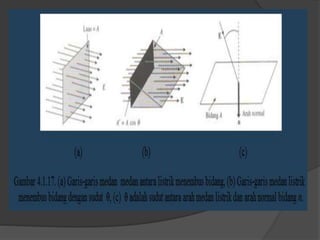
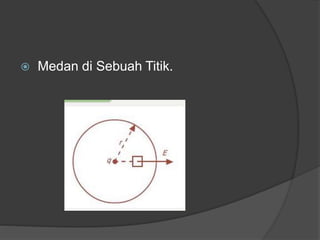
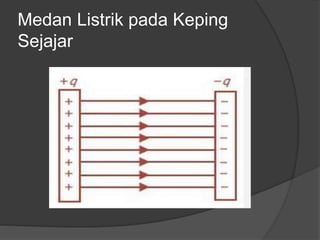
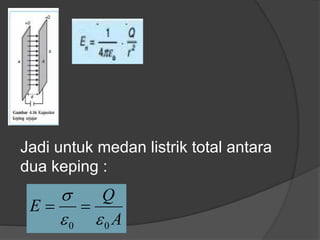
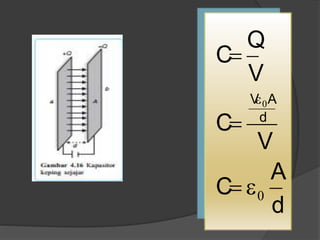
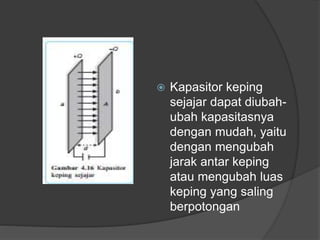
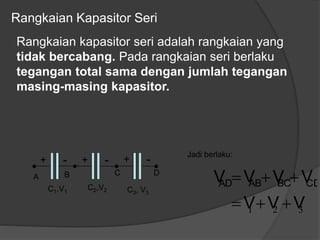
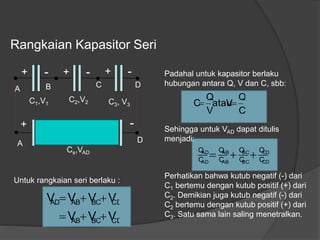
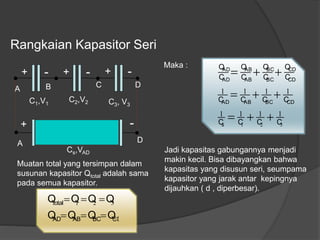
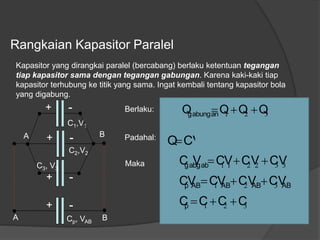
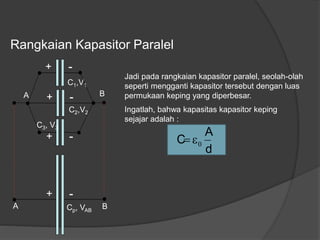
Dokumen ini membahas konsep dasar listrik statis, termasuk gaya Coulomb, medan listrik, energi potensial listrik, dan hukum Gauss, serta penerapan dalam kapasitor dan rangkaian kapasitor. Penjelasan mencakup rumus-rumus matematis terkait dengan medan listrik, beda potensial listrik, dan kapasitansi kapasitor. Selain itu, terdapat penjelasan mengenai rangkaian kapasitor seri dan paralel serta bagaimana hubungan antara muatan, tegangan, dan kapasitansi pada masing-masing jenis rangkaian.

1. Novi Suci Purwandari
Maghfira Febriana
Fita Permata Sari

2. Listrik Statis
 listrik yang tidak mengalir
Penggaris plastik
yang telah
digosok-gosok
pada rambut dapat
menarik potongan
kertas.
Why???

3. Atom
Zat
Atom
elektron
Proton
Neutron
Inti atom

5. Muatan Listrik pada Benda
Kaca  kain sutera
Plastik  kain wol

6. Hukum Coulomb
2
21
r
qq
kF 
F = gaya coulomb ( N )
q = muatan ( C )
r = jarak ( m )
k = konstanta 9.109
Nm2/C2

7. Garis Gaya Listrik
Medan listrik digambarkan oleh garis -
garis gaya listrik.

8. Medan Listrik
 Benda yang bermuatan listrik yang dikelilingi
sebuah daerah.
 Menurut Faraday (1791- 867), suatu medan
listrik keluar dari setiap muatan dan menyebar
ke seluruh ruangan.

9.  Untuk memvisualisasikan medan listrik, dilakukan
dengan menggambarkan serangkaian garis untuk
menunjukkan arah medan listrik pada berbagai titik di
ruang, yang disebut garis-garis gaya listrik

11.  secara matematis kuat medan listrik di semua titik
pada ruang dirumuskan:
Sehingga :
medan listrik pada jarak r dari satu
muatan titik Q adalah:

12. Energi Potensial Listrik

13.  besar usaha untuk memindahkan suatu muatan dari
titik a ke titik b dapat ditentukan dengan persamaan
berikut ini.

14.  Jika muatan +q' semula pada jarak tak terhingga (∼),
besar energi potensialnya adalah nol. Dengan
demikian, apabila muatan +q' dipindahkan dari
tempat yang jauh tak terhingga ke suatu titik b,
besar usahanya adalah sebagai berikut:
Sehingga :

15. Hukum Gauss
Hukum Gaus menyatakan :
“jumlah aljabar garis-garis gaya magnet (fluks)
listrik yang menembus permukaan tertutup
sebanding dengan jumlah aljabar muatan
listrik di dalam permukaan tersebut”

16. Rumus matematisnya adalah :

17.  Fluks medan listrik yang disimbolkan ΦE,
dapat dinyatakan oleh jumlah garis yang
melalui suatu penampang tegak lurus.

18. Φ = E × A
 Satuan untuk E adalah N/C, sehingga
satuan untuk fluks listrik (dalam SI)
adalah (N/C)(m2) yang dinamakan
weber (Wb). 1 weber = 1 NC-1m2

20.  Untuk medan listrik menembus bidang tidak
tegak lurus,
Φ = EA’
 Dengan A’ = A cos θ, sehingga:
Φ = EA cos θ
 Dengan θ adalah sudut antara arah E dan
arah normal bidang n. Arah normal bidang
adalah arah yang tegaklurus terhadap
bidang

21.  Medan di Sebuah Titik.

22.  Rumus matematis :
 karena k = 1/4πε0 maka persamaannya
menjadi :

23. Medan Listrik pada Keping
Sejajar

24.  medan listrik pada keping sejajar dapat
dicari dan hasilnnya menjadi :

25. Beda Potensial Listrik
 Potensial listrik yaitu energi potensial
tiap satu satuan muatan positif.
Potensial listrik termasuk besaran
skalar, dan secara matematis dapat
dirumuskan:

26.  Persamaan Ep yang telah dicari sebelumnya
disubtitusikan ke persamaan V sehingga akan
menjadi :
 Nilai q sama sehingga dapat disederhanakan
menjadi persamaan :

27. Potensial Listrik
 Usaha untuk memindahkan satu satuan
muatan positif dalam wilayah medan listrik
suatu benda (dari r1 ke r2)didefinisikan
sebagai beda potensial listrik antara
kedua titik tersebut.

28. Beda potensial listrik :
12
12
11
r
Q
k
r
Q
k
r
.Q
k
r
.Q
kV


Dalam istilah sehari-hari, beda
potensial listrik biasa disebut
dengan tegangan listrik.
Potensial lsitrik tidak dapat
diukur, sedangkan beda potensial
listrik dapat diukur, yaitu dengan
voltmeter.

29. Potensial Mutlak
r
Q
k
r
Q
k
Q
k
r
Q
kVV



 
0
1.1.
2
2
Jika muatan uji mula-mula berada di
jauh tak terhingga, maka potensial
akhirnya disebut potensial mutlak.
Jadi persamaan potensial mutlak
adalah
r
Q
kV
Q
r2

30. Potensial Listrik Total
N
N
i
itotal
V...VV
VV

 
21
1
Seperti halnya energi potensial listrik,
potensial listrik juga merupakan
besaran skalar. Jadi untuk lebih dari 1
sumber muatan, potensial totalnya
dijumlah secara aljabar biasa.
Q1 Q2
Q3
QN
1+

31. Kapasitor
Kapasitor terdiri dari susunan konduktor yang dapat
menyimpan muatan / medan / energi potensial listrik.
Kapasitor merupakan salah satu komponen
elektronika yang sering digunakan.
Kapasitor digunakan di banyak peralatan listrik
seperti radio, komputer, sistem pengapian mobil, dst.
Daya simpan muatan dalam kapasitor dinyatakan
dengan KAPASITANSI

32. Kapasitas suatu kapasitor (C) adalah
perbandingan antara besar muatan Q dari
salah satu penghantarnya dengan beda
potensial V antara kedua penghantar itu.
Keterangan :
C : kapasitansi (Farad)
Q : muatan yang
tersimpan dalam kapsitor
(C)
V : beda potensial antara
dua keping (V)
V
Q
C 

33.  Keping dapat berupa lapisan-lapisan
logam yang tipis, yang terpisah dan
terisolasi satu sama lain.
KAPASITOR KEPING SEJAJAR

34. Jadi untuk medan listrik total antara
dua keping :
A
Q
E
00 



35. Beda potensial antara a dan b :
EddlEVV
a
b
ba   .
Dapat pula di hasilkan :
d
AV
Q 0


36. d
A
C
V
C
V
Q
C
d
AV
0
0





37. Dapat disimpulkan dari
persamaan
Bahwa kapasitas kapasitor keping sejajar:
• Sebanding dengan luas keping (A)
• Berbanding terbalik dengan jarak antar keping (d)
• Sebanding dengan tetapan dielektrikum bahan di
antara keping ()
d
A
C 0

38.  Kapasitor keping
sejajar dapat diubah-
ubah kapasitasnya
dengan mudah, yaitu
dengan mengubah
jarak antar keping
atau mengubah luas
keping yang saling
berpotongan

39. Rangkaian Kapasitor Seri
Rangkaian kapasitor seri adalah rangkaian yang
tidak bercabang. Pada rangkaian seri berlaku
tegangan total sama dengan jumlah tegangan
masing-masing kapasitor.
C1,V1
C2,V2 C3, V3
+ - + - + -
A B C D
Jadi berlaku:
321 VVV
VVVV CDBCABAD



40. Rangkaian Kapasitor Seri
CDBCAB
CDBCABAD
VVV
VVVV


C
Q
Vatau
V
Q
C C1,V1
C2,V2 C3, V3
+ - + - + -
A B C D
+
A
-
D
Cs,VAD
Untuk rangkaian seri berlaku :
Padahal untuk kapasitor berlaku
hubungan antara Q, V dan C, sbb:
Sehingga untuk VAD dapat ditulis
menjadi:
CD
CD
BC
BC
AB
AB
AD
AD
C
Q
C
Q
C
Q
C
Q

Perhatikan bahwa kutub negatif (-) dari
C1 bertemu dengan kutub positif (+) dari
C2. Demikian juga kutub negatif (-) dari
C2 bertemu dengan kutub positif (+) dari
C3. Satu sama lain saling menetralkan.

41. Rangkaian Kapasitor Seri
CDBCABAD
total
QQQQ
QQQQ

 321
C1,V1
C2,V2 C3, V3
+ - + - + -
A B C D
+
A
-
D
Cs,VAD
Muatan total yang tersimpan dalam
susunan kapasitor Qtotal adalah sama
pada semua kapasitor.
Maka :
321
1111
1111
CCCC
CCCC
C
Q
C
Q
C
Q
C
Q
s
CDBCABAD
CD
CD
BC
BC
AB
AB
AD
AD



Jadi kapasitas gabungannya menjadi
makin kecil. Bisa dibayangkan bahwa
kapasitas yang disusun seri, seumpama
kapasitor yang jarak antar kepingnya
dijauhkan ( d , diperbesar).

42. Rangkaian Kapasitor Paralel
321 QQQQgabungan 
Kapasitor yang dirangkai paralel (bercabang) berlaku ketentuan tegangan
tiap kapasitor sama dengan tegangan gabungan. Karena kaki-kaki tiap
kapasitor terhubung ke titik yang sama. Ingat kembali tentang kapasitor bola
yang digabung.
C1,V1
C2,V2
C3, V3
+ -
+ -
+ -
A B
+ -
Cp, VAB
A B
Berlaku:
Padahal:
CVQ
Maka
321
321
332211
CCCC
VCVCVCVC
VCVCVCVC
p
ABABABABp
gabgab




43. Rangkaian Kapasitor Paralel
C1,V1
C2,V2
C3, V3
+ -
+ -
+ -
A B
+ -
Cp, VAB
A B
Jadi pada rangkaian kapasitor paralel, seolah-olah
seperti mengganti kapasitor tersebut dengan luas
permukaan keping yang diperbesar.
Ingatlah, bahwa kapasitas kapasitor keping
sejajar adalah :
d
A
C 0

44. Analisis Kasus

45. TERIMA KASIH