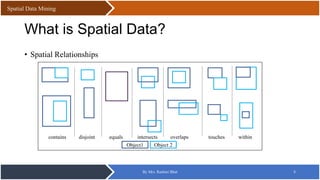
This document discusses spatial data mining. It defines spatial data as data pertaining to the geographic location of features and boundaries on Earth. Spatial data mining involves discovering patterns from large spatial datasets and can be used for applications like GIS, geomarketing, and natural disaster prediction. Some key techniques of spatial data mining include spatial classification, clustering, and detecting trends and autocorrelation. The document also discusses spatial data structures like grids, R-trees, and z-ordering which are used to store and index spatial data.

1. Spatial Data Mining
Mrs. Rashmi Bhat

2. What is Spatial Data?
• Data pertaining to the space occupied objects
• Data that identifies the geographic location of features and boundaries on Earth
• E.g. roadmap indicating cities, roads etc.
• Spatial database stores large amount of spatial data such as maps, pre-processed
remote sensing or medical imaging data.
• Spatial database have topological and distance information
• Requires spatial indexing, data access, reasoning, geometric computation and knowledge
representation techniques.
By Mrs. Rashmi Bhat 2
Spatial Data Mining

3. What is Spatial Data?
• Two distinct types of attributes
• Non-spatial attributes
• Independent of geometric considerations
• Same as in traditional data mining
• Numerical, categorical, ordinal etc.
• E.g. City_name, City_population, City_zip
• Spatial attributes
• Includes data which is geographically referenced
• Includes location, shape, size and orientation
• Deals with neighborhood and extent
• E.g. longitude, latitude, elevation
By Mrs. Rashmi Bhat 3
Spatial Data Mining

4. What is Spatial Data?
• A spatial data object occupies a certain region of space, called its spatial extent,
which is characterized by its location and boundary.
• Spatial data can be either point data or region data.
• Point data
• A point has a spatial extent characterized completely by its location.
• It occupies no space and has no associated area or volume
• Point data consists of collection of points in multidimensional space.
• Raster data is an example of directly measured point data.
By Mrs. Rashmi Bhat 4
Spatial Data Mining

5. What is Spatial Data?
• Region data
• A region has a spatial extent with a location and a boundary.
• The location can be thought of the position of a fixed 'anchor point' for the region, such as its
centroid.
• In two dimensions, the boundary can be visualized as a line (for finite regions, a closed loop),
and in three dimensions, it is a surface.
• Region data consists of a collection of regions.
• Vector data is used to describe the geometric approximations, constructed using points, line
segments, polygons, spheres, cubes.
• E.g. roads and rivers can be represented as a collection of line segments, and countries, states,
and lakes can be represented as polygons.
By Mrs. Rashmi Bhat 5
Spatial Data Mining

6. What is Spatial Data?
By Mrs. Rashmi Bhat 6
Spatial Data Mining

7. What is Spatial Data?
• Operations performed to manipulate vector data
• Determining distance between two objects
• Determining the area of the object
• Determining the length of the object
• Determining an intersection or union of the objects
• Determining mutual positions of the two object
By Mrs. Rashmi Bhat 7
Spatial Data Mining

8. What is Spatial Data?
• Spatial Relationships
By Mrs. Rashmi Bhat 8
Spatial Data Mining
disjoint
contains equals intersects overlaps touches within
Object1 Object 2

9. What is Spatial Data?
• Spatial Relationships
By Mrs. Rashmi Bhat 9
Spatial Data Mining
Land area contains Lake & Lake is within the land
area
Two countries are disjoint
Two roads intersect each other
Front pyramid overlaps the pyramid in back
State1 touches state2

10. What is Spatial Data?
• How spatial data is represented?
• Stored as Coordinates and Topology
• Indicates latitude and longitude or depth and height
• In terms of points, lines and polygons
• Raster data
• Consists of a matrix of cells organized into rows and columns in which each
cell represents specific spatial information
• Represents data in cells or in grid matrix
• Vector Data
• Used to store data that has discrete boundaries.
• Represents data using sequential points or vertices
By Mrs. Rashmi Bhat 10
Spatial Data Mining

11. What is Spatial Data?
By Mrs. Rashmi Bhat 11
Spatial Data Mining
Fig. In-car Navigation System
Fig. Road Map

12. What is Spatial Data Mining?
• Spatial mining is the process of discovering interesting and previously unknown
but potentially useful patterns from large spatial datasets.
• It is more difficult process due to complexity of spatial data types, spatial
relationships and spatial autocorrelation.
• It demands an integration of data mining with spatial database technologies.
• It can be used for
• understanding spatial data,
• discovering spatial relationships and relationships between spatial and nonspatial data,
• constructing spatial knowledge bases,
• reorganizing spatial databases, and
• optimizing spatial queries.
By Mrs. Rashmi Bhat 12
Spatial Data Mining

13. What is Spatial Data Mining?
• Spatial Data Mining Techniques
• Spatial Classification
• Spatial Prediction
• Spatial Association Rule
• Spatial Co-location Mining
• Spatial Clustering
• Spatial Trend Detection
• Spatial Autocorrelation
By Mrs. Rashmi Bhat 13
Spatial Data Mining

14. What is Spatial Data Mining?
• Spatial Data Mining Applications
• GIS
• Geomarketing
• Remote sensing
• Navigation
• Satellite communication
• Natural disaster prediction
• Agriculture development using biodiversity
• Real estate business for land evaluation
• For environmental studies
• And many more…
By Mrs. Rashmi Bhat 14
Spatial Data Mining

15. What is Spatial Data Mining?
• How spatial data mining is different from classical data mining?
• The data input of spatial data mining are more complex than the inputs of classical data
mining
• The data input of spatial data mining have two distinct types: spatial and non-spatial
attributes
• Data input to spatial data mining are implicit in nature
• Statistical foundation for spatial data mining is spatial autocorrelation while for data mining
its independence of samples
• Output of spatial data mining is spatial interest based, while that of classical data mining its
set based.
By Mrs. Rashmi Bhat 15
Spatial Data Mining

16. Spatial Data Structures
• Spatial Indexes
• A multidimensional or spatial index, utilizes some kind of spatial relationship to organize
data, entries, with each key value seen as a point (or region, for region data) in a k-dimensional
space, where k is the number of fields in the search key for the index.
• Spatial index structures
• For point data
• Grid files, KD trees, Point Quad trees, SR trees etc.
• For region data
• Region Quad tree, R trees, and SKD trees
• R tree is widely implemented and used in commercial DBMSs
By Mrs. Rashmi Bhat 16
Spatial Data Mining

17. Spatial Data Structures
• Spatial Indexes
• Most commonly used three approaches
• Z-ordering for point data (based on space filling curve)
• Grid Files
• R trees
By Mrs. Rashmi Bhat 17
Spatial Data Mining

18. Spatial Data Structures
• Z-ordering
• Space-filling curves are based on the assumption that any attribute value can be represented
with some fixed number of bits, say k bits.
• The maximum number of values along each dimension is 2𝑘
By Mrs. Rashmi Bhat 18
Spatial Data Mining
1st iteration 2nd iteration 3rd iteration 4th iteration

19. Spatial Data Structures
• Z-ordering
By Mrs. Rashmi Bhat 19
Spatial Data Mining
1st iteration 2nd iteration 3rd iteration
0 1
2 3
0
0
1
2
0 1 4 5
2 3 6 7
8 9 12 13
10 11 14 15
0
0
1
2
4
8
10
5
0
?
?

20. Spatial Data Structures
• Z-ordering
• Z-ordering recursively decomposes the data space into quadrants and subquadrants.
• The Region quad tree structure corresponds directly to the recursive decomposition of the
data space.
• Each node in the tree corresponds to a square-shaped region of the data space.
• The root corresponds to the entire data space, and leaf nodes correspond to exactly one point.
• Each internal node has four children, corresponding to the four quadrants into which the space
corresponding to the node is partitioned:
• 00 identifies the top left quadrant,
• 01 identifies the top right quadrant,
• 10 identifies the bottom left quadrant, and
• 11 identifies the bottom right quadrant.
By Mrs. Rashmi Bhat 20
Spatial Data Mining

21. Spatial Data Structures
• Z-ordering
By Mrs. Rashmi Bhat 21
Spatial Data Mining
0 1 4 5
2 3 6 7
8 9 12 13
10 11 14 15
00
00
01
01
10
10
11
11
11
0 1 2 3
00 01 10 11
00 01 10 11
12 13 14 15
01 10 11
00
. . .
Z-Ordering
Region Quad Tree

22. Spatial Data Structures
• Grid Files
• Grid cells represents or defines a class, group, category or membership
By Mrs. Rashmi Bhat 22
Spatial Data Mining

23. Spatial Data Structures
• R-Tree
• Groups nearby objects and represents them with their minimum bounding rectangle (MBR) in
the next higher level of the tree
• “R” in R-tree stands for rectangle.
• Nodes of the tree store MBRs of objects or collections of objects
• The leaf nodes of the R-tree store the exact MBRs or bounding boxes of the individual
geometric objects, along with a pointer to the storage location of the contained geometry.
• All non-leaf nodes store references to several bounding boxes for each of which is a pointer to
a lower level node.
• The tree is constructed hierarchically by grouping the leaf boxes into larger, higher level boxes
which may themselves be grouped into even larger boxes at the next higher level.
By Mrs. Rashmi Bhat 23
Spatial Data Mining

24. Spatial Data Structures
• R-Tree
By Mrs. Rashmi Bhat 24
Spatial Data Mining

25. Spatial Data Structures
• R-Tree
• The tree is constructed hierarchically by grouping the leaf boxes into larger, higher level boxes
which may themselves be grouped into even larger boxes at the next higher level.
• Since the original boxes are never sub-divided, as a consequence the non-leaf node ‘covering
boxes’ can be expected to overlap each other.
By Mrs. Rashmi Bhat 25
Spatial Data Mining

26. Spatial Autocorrelation
• Spatial Autocorrelation
• “Everything is related to everything else but nearby things are more related than distant
things”
• Spatial autocorrelation defines measures how much close objects are in comparison with other
close objects in space
• Moran’s I classifies:
By Mrs. Rashmi Bhat 26
Spatial Data Mining
Positive Spatial
Autocorrelation
No Spatial
Autocorrelation
Negative Spatial
Autocorrelation

27. Mining Spatial Associations
• Similar to the mining of association rules in transactional and relational databases,
spatial association rules can be mined in spatial databases.
• A spatial association rule is of the form of
𝐴 ⇒ 𝐵 𝑠%, 𝑐%
where
• 𝐴 and 𝐵 are sets of spatial or nonspatial predicates,
• 𝑠% is the support of the rule, and 𝑐% is the confidence of the rule.
• e.g. the following is a spatial association rules
𝒊𝒔_𝒂(𝑿, "𝑺𝒄𝒉𝒐𝒐𝒍") ∧ 𝒄𝒍𝒐𝒔𝒆_𝒕𝒐(𝑿, "𝒔𝒑𝒐𝒓𝒕_𝒄𝒆𝒏𝒕𝒆𝒓") ⇒ 𝒄𝒍𝒐𝒔𝒆_𝒕𝒐(𝑿, "𝒑𝒂𝒓𝒌") [𝟎. 𝟓%, 𝟖𝟎%]
• This rule states that 80% of schools that are close to sports centers are also close to parks, and 0.5% of
the data belongs to such a case.
By Mrs. Rashmi Bhat 27
Spatial Data Mining

28. Mining Spatial Associations
• Examples include distance information (such as 𝑐𝑙𝑜𝑠𝑒_𝑡𝑜 and 𝑓𝑎𝑟_𝑎𝑤𝑎𝑦), topological
relations (like 𝑖𝑛𝑡𝑒𝑟𝑠𝑒𝑐𝑡, 𝑜𝑣𝑒𝑟𝑙𝑎𝑝, and 𝑑𝑖𝑠𝑗𝑜𝑖𝑛𝑡), and spatial orientations (like 𝑙𝑒𝑓𝑡_𝑜𝑓 and
𝑤𝑒𝑠𝑡_𝑜𝑓).
• Spatial association mining needs to evaluate multiple spatial relationships among a
large number of spatial objects, the process could be quite costly.
• An interesting mining optimization method called progressive refinement can be
adopted in spatial association analysis.
• The method first mines large data sets roughly using a fast algorithm and then improves the
quality of mining in a pruned data set using a more expensive algorithm.
By Mrs. Rashmi Bhat 28
Spatial Data Mining

29. Mining Spatial Associations
• How to ensure the pruned data set covers the complete set of answers?
• an important requirement for the rough mining algorithm applied in the early stage is the
superset coverage property: that is, it preserves all of the potential answers.
• It should allow the false positive test, which might include some data sets that do not belong
to the answer sets
• It should not allow a false-negative test, which might exclude some potential answers.
• e.g. For mining spatial associations related to the spatial predicate close_to, collect
the candidates that pass the minimum support threshold by
• Applying certain rough spatial evaluation algorithms
• Evaluating the relaxed spatial predicate, g_close_to, which is a generalized close_to covering a
broader context that includes close_to, touch, and intersect.
By Mrs. Rashmi Bhat 29
Spatial Data Mining

30. Mining Spatial Associations
• If two spatial objects are closely located, their enclosing MBRs must be closely located,
matching g_close_to.
• The reverse is not always true: if the enclosing MBRs are closely located, the two spatial
objects may or may not be located so closely.
• The MBR pruning is a false-positive testing tool for closeness.
• Spatial Co-location Mining
• Identifying groups of particular features that appear frequently close to each other in a
geospatial map.
• Finding spatial co-locations can be considered as a special case of mining spatial associations.
• Based on the property of spatial autocorrelation, interesting features likely to coexist in closely
located regions.
By Mrs. Rashmi Bhat 30
Spatial Data Mining

31. Spatial Clustering
• Spatial data clustering identifies clusters, or densely populated regions, according
to some distance measurement in a large, multidimensional data set.
• Spatial clustering is a process of grouping a set of spatial objects into clusters so
that objects within a cluster have high similarity in comparison to one another, but
are dissimilar to objects in other clusters.
• e.g. Hot spot analysis in crime analysis and disease tracking
By Mrs. Rashmi Bhat 31
Spatial Data Mining

32. By Mrs. Rashmi Bhat 32
Spatial Data Mining

33. Spatial Clustering
• CLARANS (Clustering Large Applications based upon RANdomized Search)
• Combines the sampling technique (CLARA) with PAM
• Aims to use randomized search to facilitate the clustering of a large number of objects
• CLARANS draws a sample with some randomness in each step of the search.
• This clustering process can be viewed as a search through a graph, where each node is a
potential solution (a set of k-medoids).
• Two nodes are neighbors (connected by an arc in the graph) if their sets differ by only one
object.
• Each node can be assigned a cost that is defined by the total dissimilarity between every object
and the medoid of its cluster.
• At each step, PAM examines all of the neighbors of the current node in its search for a
minimum cost solution.
• The current node is then replaced by the neighbor with the largest descent in costs.
By Mrs. Rashmi Bhat 33
Spatial Data Mining

34. Spatial Clustering
• CLARANS (Clustering Large Applications based upon RANdomized Search)
• CLARANS dynamically draws a random sample of neighbors in each step of a search.
• The number of neighbors to be randomly sampled is restricted by a userspecified parameter.
• If a better neighbor is found (i.e., having a lower error), CLARANS moves to the neighbor’s
node and the process starts again; otherwise, the current clustering produces a local minimum.
• If a local minimum is found, CLARANS starts with new randomly selected nodes in search
for a new local minimum.
• Once a user-specified number of local minima has been found, the algorithm outputs, as a
solution, the best local minimum, that is, the local minimum having the lowest cost.
• CLARANS also enables the detection of outliers
• The computational complexity of CLARANS is about 𝑂(𝑛2
)
By Mrs. Rashmi Bhat 34
Spatial Data Mining