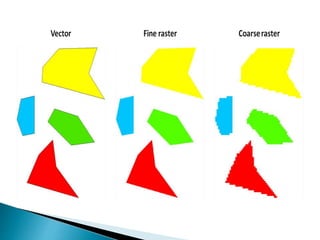
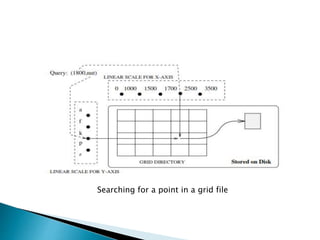
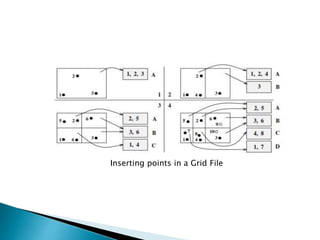
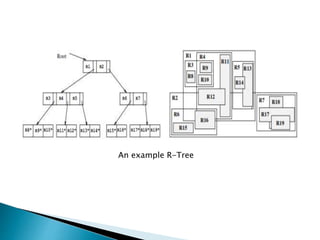
The document provides an overview of spatial data, including its definitions, types, queries, and indexing techniques. It discusses applications such as Geographic Information Systems (GIS) and multimedia databases, while comparing various indexing methods like R-trees, grid files, and region quad-trees. The challenges of managing high-dimensional spatial data and the use of spatial data in different database management systems are also highlighted.

1. By-
Neha Kulkarni
ME Computer
Pune Insitute of Computer Technology

2.  What is spatial data?
 Types of spatial data
 Types of queries
 Applications
 Indexing Techniques
 Comparison of Indexing techniques
 GiST
 Indexing High-dimensional data
 Conclusion

3. • Spatial data represent the location ,size
and shape of an object on earth
• Ex. Building, lake

4. Point data: Line data: polygon data:

5.  Point Data:
 Simplest form of representing spatial data
 No space and has no associated area or volume
 Consists of collection of points
 Ex. Raster data

6.  Region data:
 Has spatial extend with location and boundaries
 Represented using of points, line, polygons
 Ex. roads, rivers: line data

8. 1) Spatial range queries:
Related with region data
Ex. “Find all cities within 50 miles of Pune”
2)Nearest Neighbor queries:
Related with point data
Ex. “Find 10 cities nearest to Pune”
In ordered cities
Use in multimedia database

9. 3) Spatial Join Queries:
- use both point and region data.
- Ex. “Find pairs of cities within 200 miles of each other
AND “ Find all cities near a lake”
- More complex
- Expensive to evaluate

10. 1) Geographic Information System(GIS)
Ex. MAP
2) Computer Aided Design/Manufacturing(CAD/CAM)
Ex. Surface of design object
Range and Spatial join queries used
3) Multimedia Database
video, audio, image, text also required spatial data
Nearest neighbor queries and point data

11. Point Data: Grid files, ḥE trees, Kdtrees, point quad
trees
Region data: Quad trees, R trees, SKD trees,
-Yet no best indexing technique
- R trees are commonly used :
due to simplicity, ability to handle both data
performance to complex queries

12. Three main indexing techniques :
 Region Quad-Trees and Z-Ordering – handle
both point and region data
 Grid Files – only point data
 R-Trees – handle both point and region data

13.  Z-ordering gives us a way to group points
according to spatial proximity.
 Consider X-01 and Y-11
 Z-value is 0111 by interleaving
X and Y values.
This gives us the value for the
point 7.
Space filling curves

14. The Region Quad tree structure corresponds directly to the
recursive decomposition of the data space.
Each node in the tree corresponds to a square-shaped region of
the data space.

15.  Grid files rely upon a grid directory to identify the
data page containing a desired point.
 The Grid file partitions space into rectangular
regions using lines that are parallel to the axes.
 If the X axis is cut into i segments and the Y
axis is cut into j segments, we have a total of i
x j partitions. The grid directory is an i by j
array with one entry per partition.
 This description is maintained in an array
called a linear scale; there is one linear scale
per axis.

16. Searching for a point in a grid file

17. Inserting points in a Grid File

18.  Adaptation of B+ Tree
 Height-balanced data structure
 Search key values are referred to as Bounding
Boxes
 A data entry consists of a pair (n-dimensional
box, Rid)
 Rid – object Identifier
 N-dimensional box is the smallest box that
contains the object

19. An example R-Tree

20.  Search for Objects Overlapping Box Q
Start at root.
1. If current node is non-leaf, for each
entry <E, ptr>, if box E overlaps Q,
search subtree identified by ptr.
2. If current node is leaf, for each entry
<E, rid>, if E overlaps Q, rid identifies
an object that might overlap Q.

21. Insert Entry <B, ptr>
 Start at root and go down to “best-fit” leaf L.
 Go to child whose box needs least enlargement to
cover B; resolve ties by going to smallest area child.
 If best-fit leaf L has space, insert entry and stop.
Otherwise, split L into L1 and L2.
 Adjust entry for L in its parent so that the box now
covers (only) L1.
 Add an entry (in the parent node of L) for L2. (This
could cause the parent node to recursively split.)

22. Region Quad
Trees
Grid Files(point
data)
R-Trees
Range Queries Easily handled Easily handled
for point data.
Handled by
calculating
bounding box
Nearest
Neighbour
Queries
Can be
handled.
Sometimes
tricky due to
long diagonal
jumps
Easily handled
for point data.
Handled well
by traversing
for the point
or region
Spatial Joins Can be
handled with
some
extension to
range queries
Easily handled
for point data.
Handled very
well

23.  The Generalized Search Tree (GiST) abstracts the
“tree” nature of a class of indexes including B+ trees
and R-tree variants.
 Striking similarities in insert/delete/search and even
concurrency control algorithms make it possible to
provide “templates” for these algorithms that can be
customized to obtain the many different tree index
structures.
 GiST provides an alternative for implementing other
tree indexes in an ORDBMS.

24.  Typically, high-dimensional datasets are collections
of points, not regions.
 E.g., Feature vectors in multimedia applications.
 Very sparse
 Nearest neighbor queries are common.
 R-tree becomes worse than sequential scan for most
datasets with more than a dozen dimensions.
 As dimensionality increases contrast (ratio of
distances between nearest and farthest points)
usually decreases; “nearest neighbor” is not
meaningful.

25.  Spatial data management has many
applications, including GIS, CAD/CAM,
multimedia indexing, Point and region data
 R-tree approach is widely used in GIS
systems
 Used in spatial data mining approaches.
 Popular SDBMS : MySQL(geometry datatype),
Neo4j, AllegroGraph, SpaceBase, CouchDB,
PostGreSQL, SpatialDB

26.  “Database Management Systems” by Raghu
Ramakrishnan, 3rd Edition
 www.techopedia.com/definition
 dna.fernuni-hagen.de/IntroSpatialDBMS
 www.geol-amu.org/notes