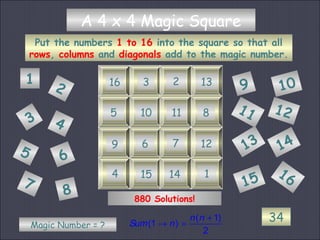
The document discusses magic squares, which are grids of numbers arranged so that the sums of each row, column and diagonal are equal. It provides examples of 3x3 and 4x4 magic squares and notes that magic squares were historically used for protection and as amulets. It also highlights some unique magic squares, including one created by Benjamin Franklin that contains interesting additional features beyond just the row/column/diagonal sums.

1.  NAME: DHRUV SOLANKI
 CLASS:VIII – A
 ROLL NO. : 7
 SUBJECT: MATHS

2. Magic Squares
A 3 x 3 magic Square
Put the numbers 1 to 9 into the square so that all rows,
columns and diagonals add to the magic number.
1
2
Magic Number = ?
3
6 5
4
7
8
9
4
7
5 3
9

3. 15
( 1)
(1 )
2
n n
Sum n
+
→ =
Magic Squares
A 3 x 3 magic Square
Put the numbers 1 to 9 into the square so that all rows,
columns and diagonals add to the magic number.
Magic Number = ?
1
2 3
6 5
4
7
8
9
51 9
2
8
6
43
7

4. In the Middle Ages magic squares were believed to give
protection against the plague!
In the 16th
Century, the Italian mathematician, Cardan,
made an extensive study of the properties of magic
squares.
During this century they have been used as amulets in
India.
Even today they are widespread in Tibet, (appearing in
the “Wheel of Life) and in other countries such as
Malaysia, that have close connections with China and
India.

5. A 4 x 4 Magic Square
( 1)
(1 )
2
n n
Sum n
+
→ =
Put the numbers 1 to 16 into the square so that all
rows, columns and diagonals add to the magic number.
1
Magic Number = ?
2
3 4
5 6
7
8
9 10
11 12
13 14
15
16
880 Solutions!
34
10 11
6 7
15 14
8
129
16
1
13
4
5
3 2

6. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
The Melancholia Magic Square
The melancholia magic
square is highly
symmetrically with
regard to its magic
constant of 34. Can you
find other groups of
cells that give the
same value?
34

7. An Amazing Magic Square!
7 12 1 14
2 13 8 11
16 3 10 5
9 6 15 4
This magic square
originated in
India in the 11th
or 12th
century
How many 34’s can you find?

8. Benjamin Franklin’s Magic Square.
The American statesman, scientist, philosopher, author
and publisher created a magic square full of interesting
features.
Benjamin was born in Massachusetts and was the 15th
child
and youngest son of a family of seventeen. In a very full
life he investigated the physics of kite flying.