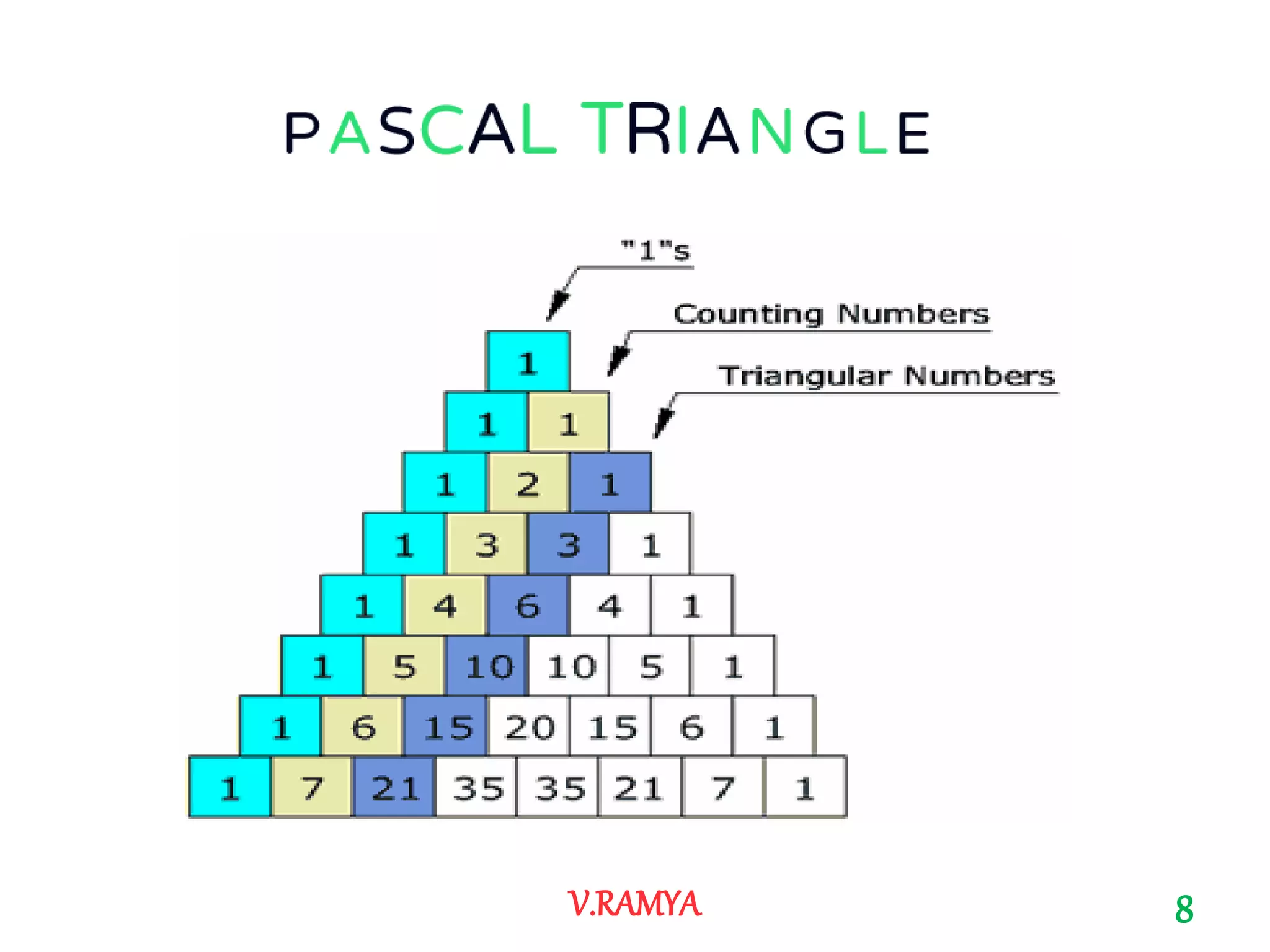
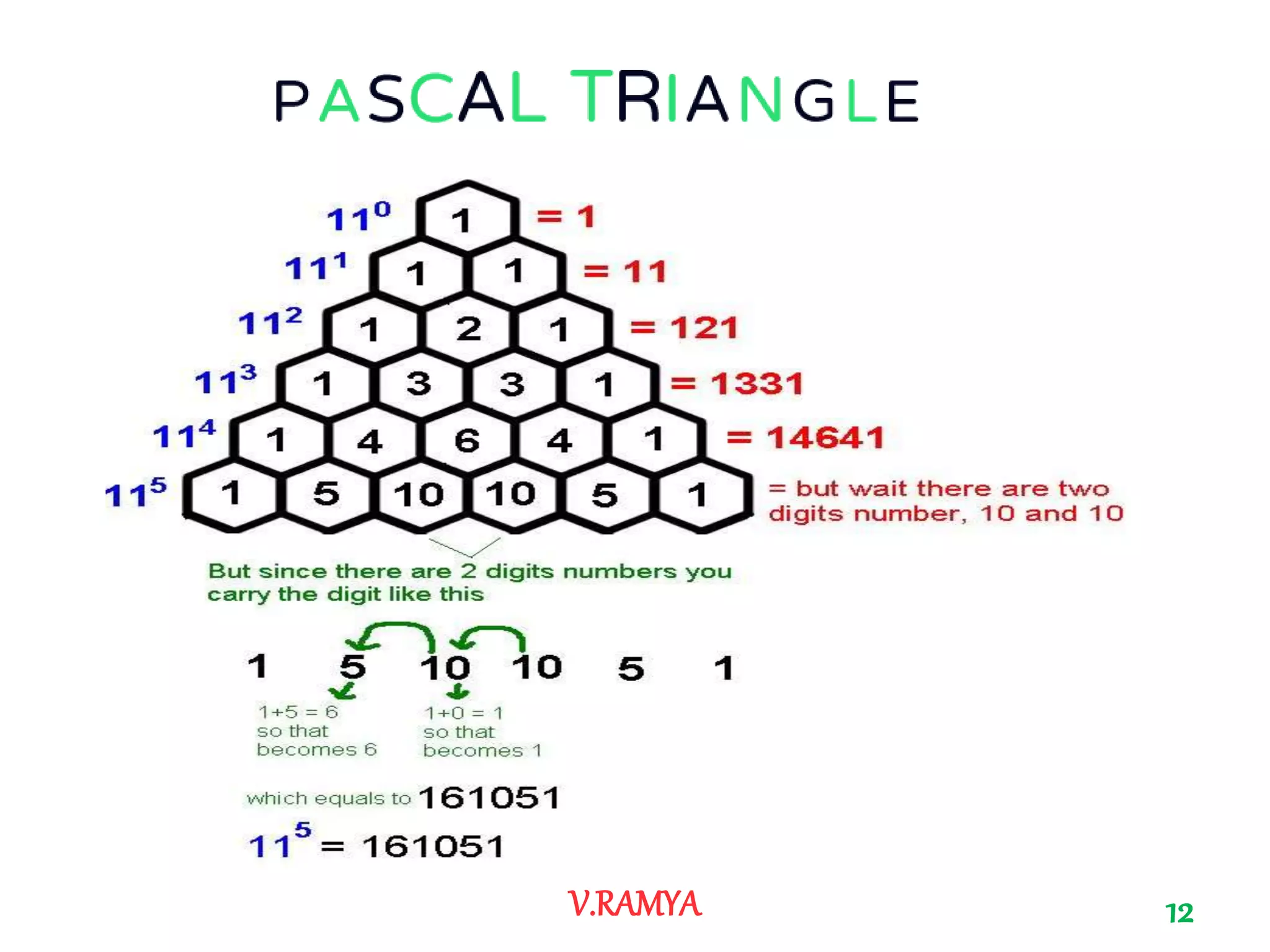
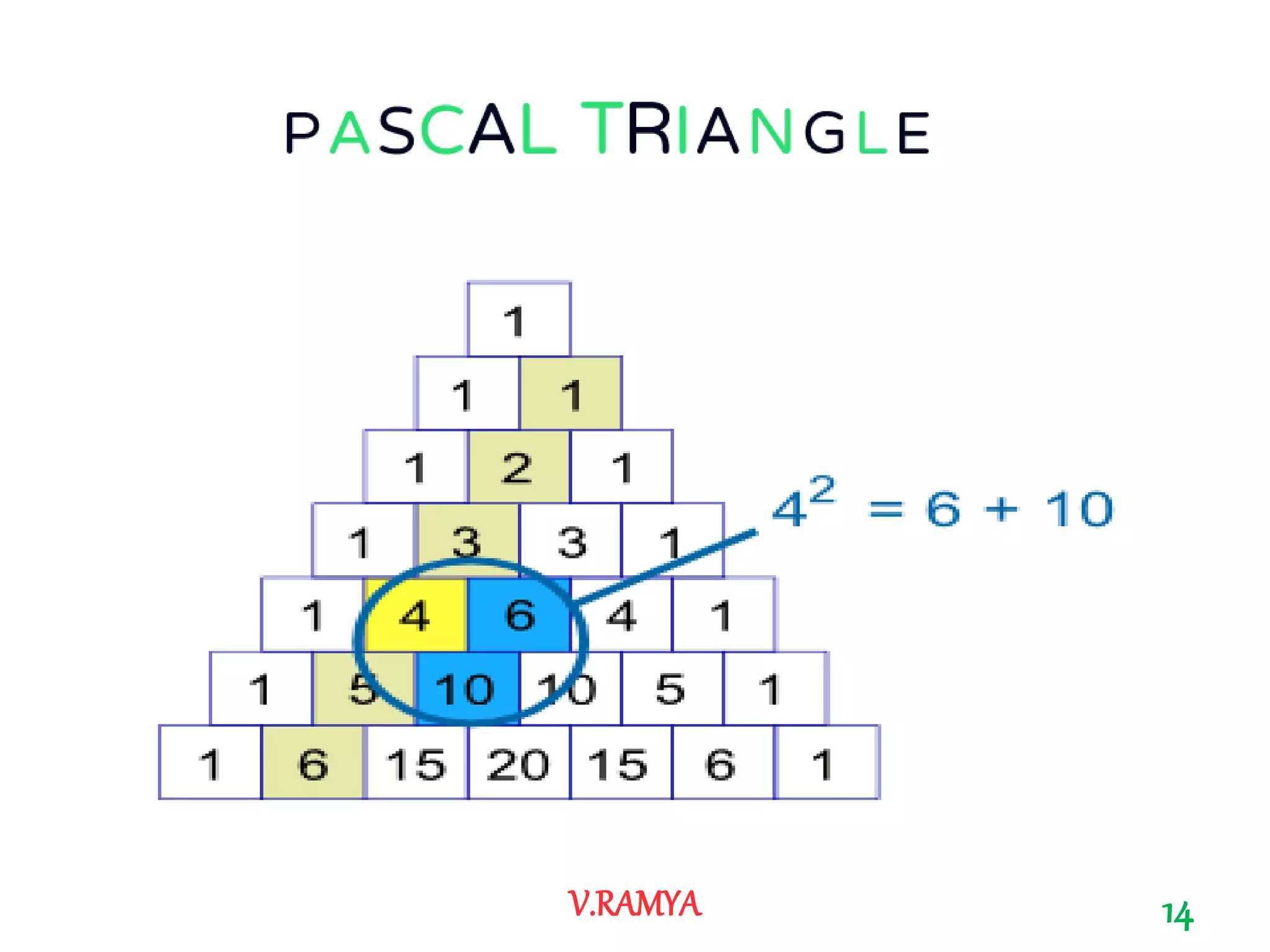
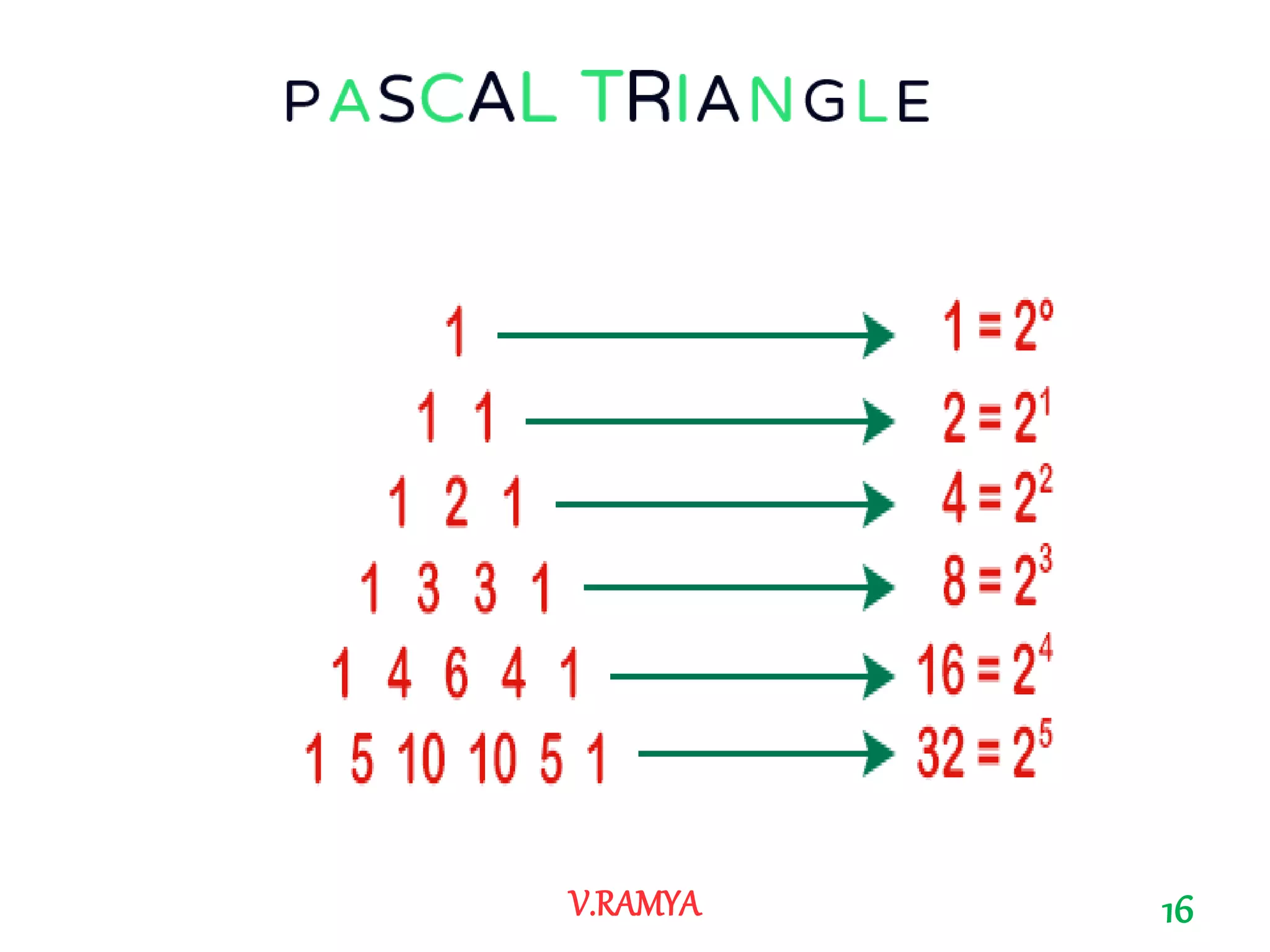
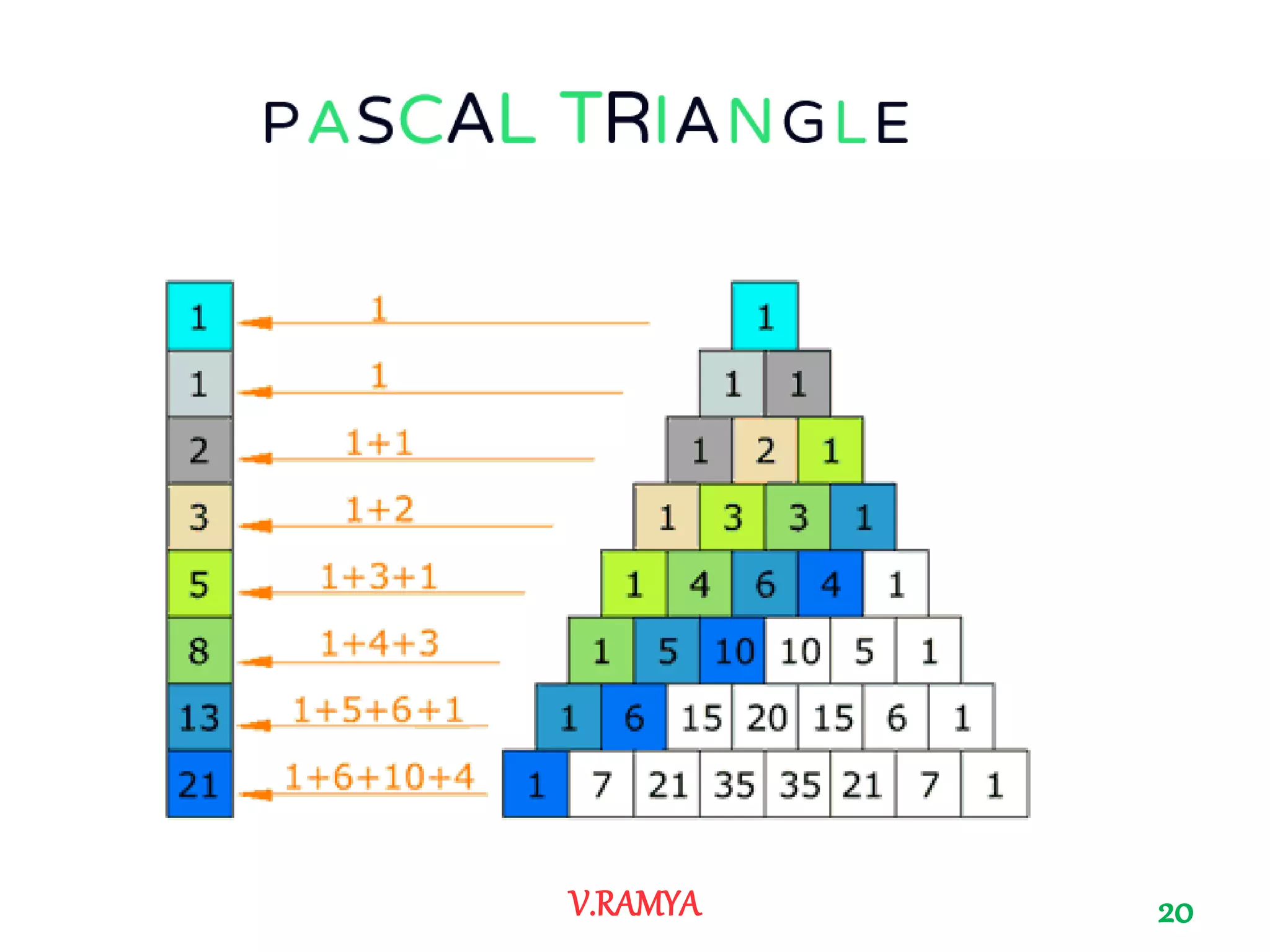
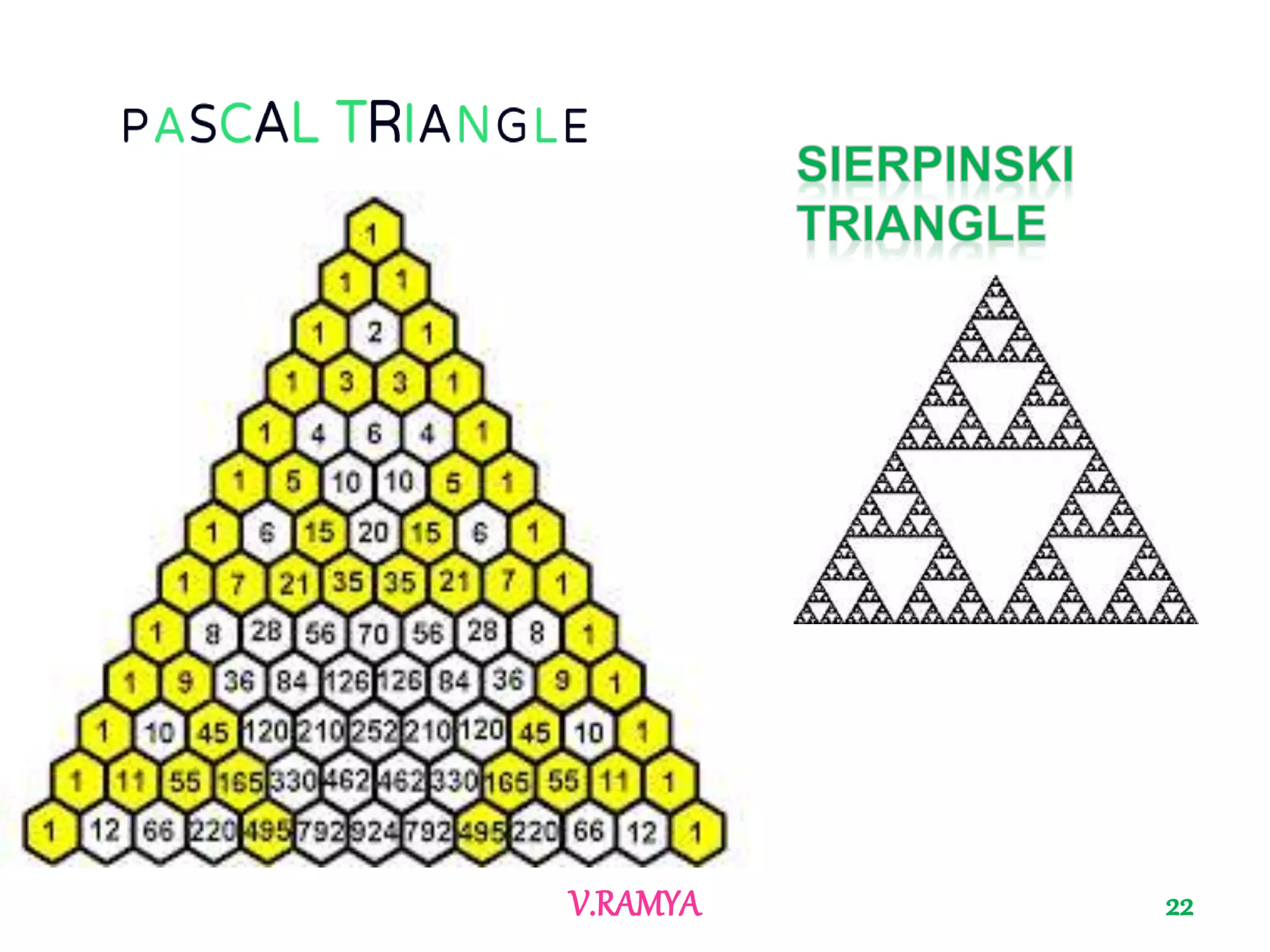
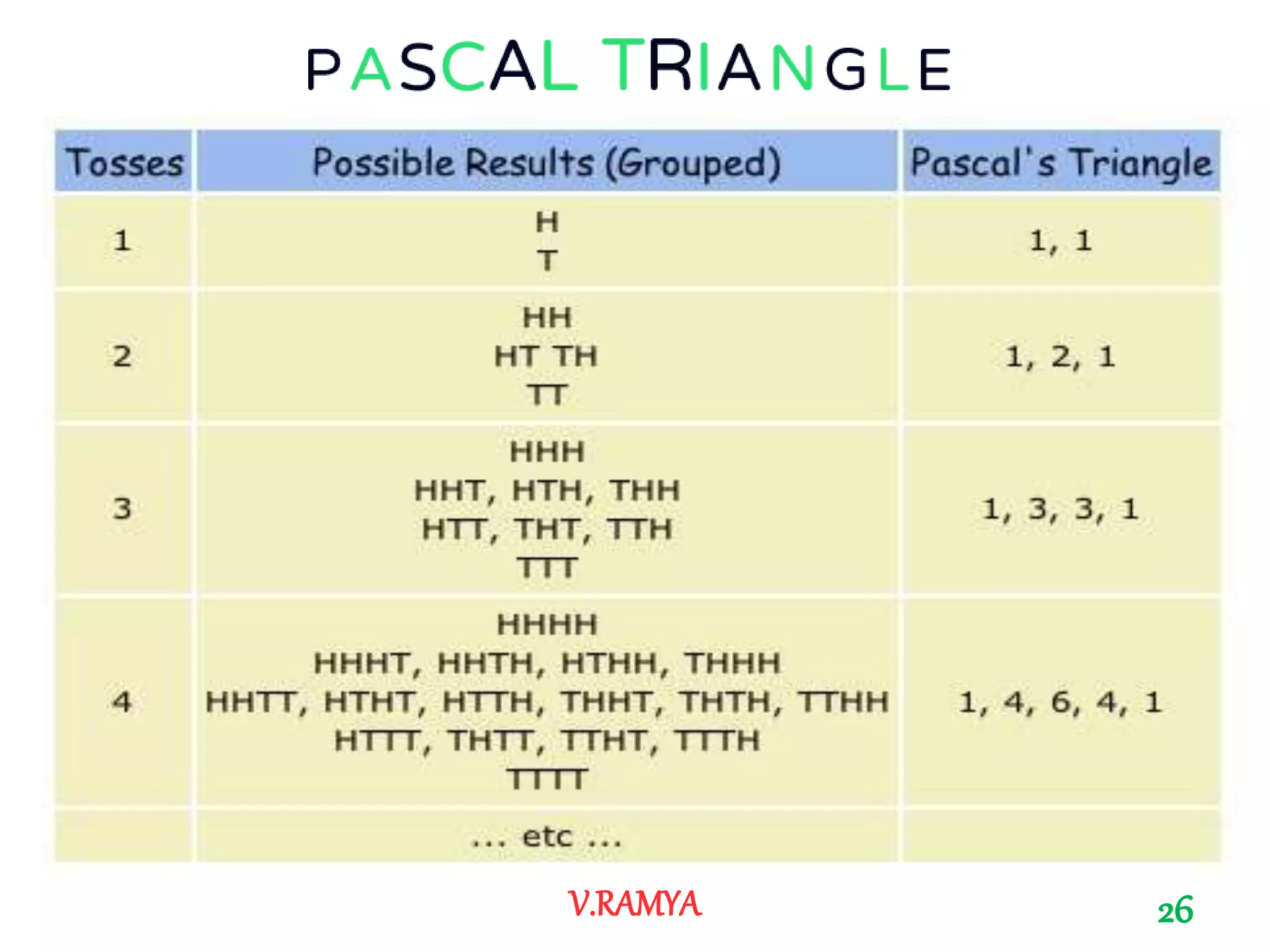
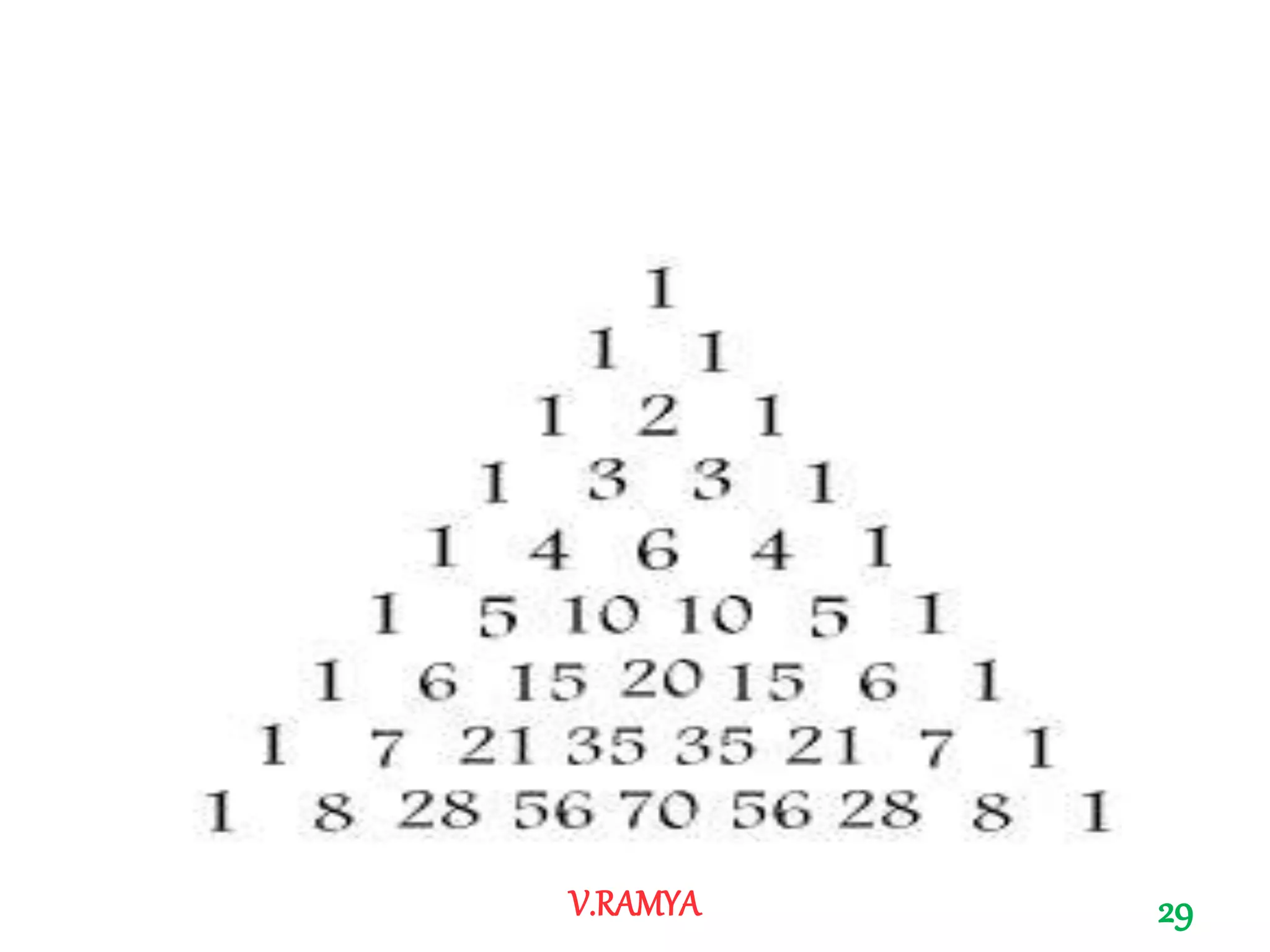
The document discusses Pascal's triangle, named after Blaise Pascal. It describes how to construct the triangle by placing numbers in a triangular pattern where each number is the sum of the two numbers above it. Some key properties mentioned include the triangle's symmetry, relationships between diagonals and powers of numbers, and how it can be used to show combinations and coefficients in binomial expansions.

1. 1V.RAMYA

2. 2V.RAMYA

3. 3V.RAMYA
• Blaise Pascal, a famous French
Mathematician and Philosopher.

4. 4V.RAMYA

5. • One of the most interesting Number
Patterns is Pascal's Triangle (named
after Blaise Pascal, a famous French
Mathematician and Philosopher).
• To build the triangle, start with "1" at
the top, then continue placing numbers
below it in a triangular pattern.
Each number is the numbers directly
above it added together.
5V.RAMYA

6. 6V.RAMYA

7. • The first diagonal is, of course, just "1"s
• The next diagonal has the Counting
Numbers (1,2,3, etc).
• The third diagonal has the triangular
numbers
• (The fourth diagonal, not highlighted, has
the tetrahedral numbers.)
7V.RAMYA

8. 8V.RAMYA

9. • The triangle is also symmetrical. The
numbers on the left side have identical
matching numbers on the right side,
like a mirror image.
9V.RAMYA

10. 10V.RAMYA

11. • Each line is also the powers
(exponents) of 11:
• 110=1 (the first line is just a "1")
• 111=11 (the second line is "1" and "1")
• 112=121 (the third line is "1", "2", "1")
• etc!
11V.RAMYA

12. 12V.RAMYA

13. • For the second diagonal, the square of a
number is equal to the sum of the
numbers next to it and below both of
those.
• Examples:
• 32 = 3 + 6 = 9,
• 42 = 6 + 10 = 16,
• 52 = 10 + 15 = 25,
13V.RAMYA

14. 14V.RAMYA

15. The sum of the numbers in any row
is equal to 2 to the nth power or 2n,
when n is the number of the row. For
example:
20 = 1
21 = 1+1 = 2
22 = 1+2+1 = 4
23 = 1+3+3+1 = 8
24 = 1+4+6+4+1 = 16
15V.RAMYA

16. 16V.RAMYA

17. • The hockey stick pattern of Pascal's
triangle shows sums of numbers in the
triangle that appear as hockey sticks.
The numbers descend in a slanted
format at first, then it slants to form the
shape of a hockey stick where the
number in the slanted portion is the
sum of the numbers that descended
diagonally.
17V.RAMYA

18. 18V.RAMYA

19. • Fibonacci Sequence sum the
diagonals of the left-justified Pascal
Triangle.
19V.RAMYA

20. 20V.RAMYA

21. • Using the original orientation of
Pascal’s Triangle, shade in all the odd
numbers and you’ll get a picture that
looks similar to the famous fractal
Sierpinski Triangle.
21V.RAMYA

22. V.RAMYA 22

23. V.RAMYA 23

24. 24V.RAMYA

25. • Pascal's Triangle can show you how
many ways can
combine.
• if you toss a coin three times, there is
only one combination that will give you
three heads (HHH), but there are three
that will give two heads and one tail
(HHT, HTH, THH), also three that give one
head and two tails (HTT, THT,TTH) and
one for all Tails (TTT) .This is the pattern
"1,3,3,1" in Pascal's Triangle.
25V.RAMYA

26. 26V.RAMYA

27. • Pascal's Triangle can also show you
the coefficients in binomial expansion
27V.RAMYA

28. 28V.RAMYA

29. 29V.RAMYA

30. V.RAMYA 30

31. 31V.RAMYA

32. 32V.RAMYA