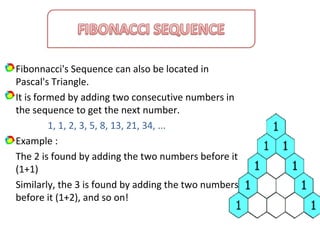
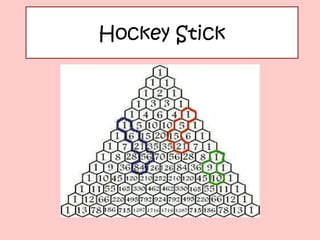
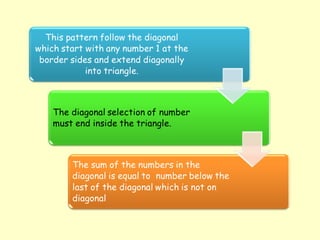
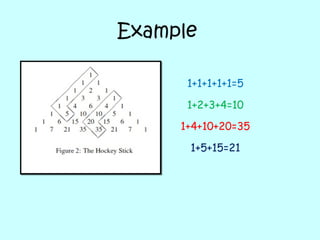
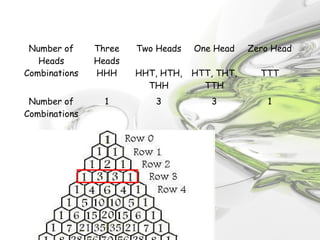
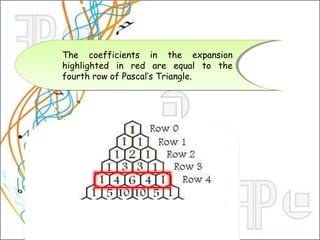
The document discusses Pascal's triangle, a mathematical pattern named after French mathematician Blaise Pascal. It contains properties like the Fibonacci sequence and uses like binomial expansion. Pascal was not the first to document the triangle - others like the Persians and Chinese used it earlier. The document also explains how Pascal's triangle can be used to calculate combinations and probabilities in events like coin tosses.

1. GROUP MEMBERS :
NUR FARALINA BINTI ASRAB ALI
(D20101037415)
NOOR AZURAH BINTI ABDUL RAZAK
(D20101037502)
NUR WAHIDAH BINTI SAMI’ON
(D20101037525)

2. The Pascal’s Triangle is one of the most
interesting number patterns in
mathematicians.
Pascal's triangle is named after the French
mathematician and philosopher, Blaise Pascal
(1623-62), who wrote a Treatise on the
Arithmetical Triangle describing it.
However, Pascal was not the first to draw out
this triangular but the Persian and Chinese
also used it even in the eleventh century
before the birth of Pascal.

3. In 1654, Blaise Pascal completed the Traite du
Triangle erithmetique, which has properties and
applications of the triangle.
Pascal had made lots of other contributions to
mathematics but the writings of his triagle are
very famous.

4. Fibonnacci's Sequence can also be located in
Pascal's Triangle.
It is formed by adding two consecutive numbers in
the sequence to get the next number.
1, 1, 2, 3, 5, 8, 13, 21, 34, ...
Example :
The 2 is found by adding the two numbers before it
(1+1)
Similarly, the 3 is found by adding the two numbers
before it (1+2), and so on!

5. Hockey Stick

6. History
It is called hockey
stick rule since the
numbers involved form
a long straight line like
the handle of the
hockey stick and the
quick turn at the end
where the sum appear
is like the part of the
contact the puck.

8. Example
1+1+1+1+1=5
1+4+10+20=35
1+2+3+4=10
1+5+15=21

9. Odd and Even

11.  Pascal’s Triangle can be used to show how
many different combinations of heads and
tails are possible depending on the number of
throws.
The number of throws is equal to the row
number in Pascal’s Triangle. For example, with
five throws look at row five and so on.
The elements in a row show how many
combinations for each possible result there
are. The possible results for five throws are
to get between five heads and zero heads

12.  Elements zero shows how many
combinations result in five heads and zero
tails, element one shows how many
combinations result in four head and one tail.
 Example :
Throw a coin three times. There shows the
table of combinations.
Throw a coin three times. There shows the
table of combinations.

13. Number of
Heads
Three
Heads
Two Heads One Head Zero Head
Combinations HHH HHT, HTH,
THH
HTT, THT,
TTH
TTT
Number of
Combinations
1 3 3 1

14. Pascal’s Triangle can also be use for binomial
expansion. The number in the nth row are also
the coefficients in the expansion of (1 + X) n
Example :
If n equals to 4 then:
(X + 1)4
= 1X4
+ 4X3
+ 6X2
+ 4X +1
If n equals to 4 then:
(X + 1)4
= 1X4
+ 4X3
+ 6X2
+ 4X +1

15. The coefficients in the expansion
highlighted in red are equal to the
fourth row of Pascal’s Triangle.
The coefficients in the expansion
highlighted in red are equal to the
fourth row of Pascal’s Triangle.

16. http://www.mathsisfun.com/numbers/fibonacci-
sequence.html
http://ptri1.tripod.com/