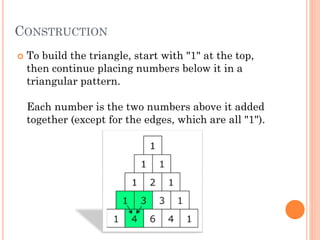
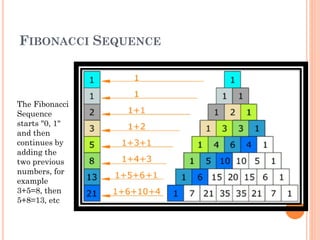
This document discusses Pascal's triangle and its relationship to the Fibonacci sequence. It explains that Pascal's triangle is an ancient mathematical pattern where each number is the sum of the two numbers above it. The diagonals of the triangle relate to important numerical sequences like the counting numbers, triangular numbers, and the Fibonacci sequence. The document also outlines various properties of Pascal's triangle, such as the horizontal rows summing to powers of two and representing powers of eleven. It provides examples of how Pascal's triangle can be used to solve probability and binomial expansion problems.

1. PASCAL S TRIANGLE AND FIBONACCI
ΔΙΑΘΕΜΑΤΙΚΗ ΔΡΑΣΗ: ΑΓΓΛΙΚΑ +ΜΑΘΗΜΑΤΙΚΑ
ΤΜΗΜΑ Γ3
Π.Π. ΓΥΜΝΑΣΙΟ ΙΩΝΙΔΕΙΟΥ ΣΧΟΛΗΣ ΠΕΙΡΑΙΑ 2014 2015
Ιωάννα Λύρα
Βίκτωρ Μαρτίνος
Μυρτώ Φιλιππάκη
Βασίλης Μιχαλίτσης
Σακκάς Γιώργος
Μαρίνης Στέλιος

2. HISTORY
 Pascal s triangle is perhaps the most
famous of all number patterns. It is
very ancient standing, being
probably more than a thousand year
old. Its hidden properties have been
revealed more and more as
mathematics has developed through
the centuries.
 The Chinese Knew About It
This drawing is entitled "The Old
Method Chart of the Seven
Multiplying Squares".
It is from the front of Chu Shi-
Chieh's book "Ssu Yuan Yü Chien"
(Precious Mirror of the Four
Elements), written in AD 1303 (over
700 years ago, and more than 300
years before Pascal!), and in the
book it says the triangle was known

3. CONSTRUCTION
 To build the triangle, start with "1" at the top,
then continue placing numbers below it in a
triangular pattern.
Each number is the two numbers above it added
together (except for the edges, which are all "1").

4. THEORY
 Pascal’s Triangle, developed by the French
Mathematician Blaise Pascal, is formed by starting with
an apex of 1. Every number below in the triangle is the
sum of the two numbers diagonally above it to the left
and the right, with positions outside the triangle counting
as zero.
 The numbers on diagonals of the triangle add to the
Fibonacci series, as shown below:

5. PATTERNS WITHIN THE TRIANGLE
 Diagonals
 The first diagonal is, of course, just "1"s, and the
next diagonal has the Counting numbers(1,2,3, etc).
 The third diagonal has the triangular numbers
 (The fourth diagonal, not highlighted, has the
tetrahedral numbers.)

6. FIBONACCI SEQUENCE
The Fibonacci
Sequence
starts "0, 1"
and then
continues by
adding the
two previous
numbers, for
example
3+5=8, then
5+8=13, etc

7. PROPERTIES
 Horizontal rows add to powers of 2 (i.e., 1, 2, 4, 8, 16,
etc.)
 The horizontal rows represent powers of 11 (1, 11, 121,
1331, 14641) for the first 5 rows, in which the numbers
have only a single digit.
 Adding any two successive numbers in the diagonal 1-
3-6-10-15-21-28… results in a perfect square (1, 4, 9,
16, etc.)
 It can be used to find combinations in probability
problems (if, for instance, you pick any two of five
items, the number of possible combinations is 10,
found by looking in the second place of the fifth
row. Do not count the 1’s.)
 When the first number to the right of the 1 in any row
is a prime number, all numbers in that row are
divisible by that prime number

8. Pascal's Triangle can also show you the
coefficients in binomial expansion

9. SOURCES
 http://www.mathsisfun.com/pascals-triangle.html
 http://www.goldennumber.net/pascals-triangle/
 H.E. HUNTLEY, The divine proportion,
Dover Publications, N.York 1970
 Α.ΑΛΙΜΠΙΝΙΣΗΣ, Σ.ΓΡΗΓΟΡΙΑΔΗΣ,
Ε.ΕΥΣΤΑΘΟΠΟΥΛΟΣ, Ν.ΚΛΑΟΥΔΑΤΟΣ,
Σ.ΠΑΠΑΣΤΑΥΡΙΔΗΣ, Α.ΣΒΕΡΚΟΣ ,
ΜΑΘΗΜΑΤΙΚΑ Γ΄ ΓΥΜΝΑΣΙΟΥ . ΟΕΔΒ,ΑΘΗΝΑ
2004