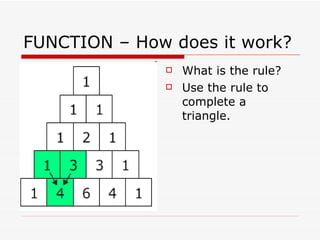
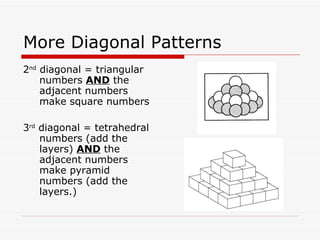
The document explores Pascal's Triangle, named after mathematician Blaise Pascal, highlighting its historical significance and its use in probability. It discusses rules for completing the triangle, patterns in row totals, and diagonal relationships such as triangular and tetrahedral numbers. Additionally, it examines the distribution of odd and even numbers, encouraging investigations into color patterns and ratios within the triangle.

1. Pascal’s Triangle WALT: investigate and describe patterns

2. What is Pascal’s triangle? Named after the French mathematician Blaise Pascal (1623-62) who brought the triangle to the attention of Western mathematicians It was known as early as 1300 in China, where it was known as the "Chinese Triangle“ It is used to solve problems of probability

3. FUNCTION – How does it work? What is the rule? Use the rule to complete a triangle.

4. What can you see? Here is a hint to help you finish the triangle. You may use a calculator.

5. Finding patterns Find the total of each row and record this. What do you notice? Can you use exponents to record this number sequence? Can you write a general statement for this number sequence?

6. Explore diagonal patterns within the triangle. Look at the diagonals: Is there a pattern along each diagonal? Describe the pattern and its rule.

7. More Diagonal Patterns 2 nd diagonal = triangular numbers AND the adjacent numbers make square numbers 3 rd diagonal = tetrahedral numbers (add the layers) AND the adjacent numbers make pyramid numbers (add the layers.)

8. Investigate Pascal’s triangle – ODDS and EVENS Shade in all the even numbers in Pascal’s triangle. What do you notice? This called - The Sierpinski Triangle

9. Are there more odd or even numbers? Can you remember the addition properties of odd and even numbers? ODD + ODD = EVEN + ODD = EVEN +EVEN = How can you relate this to your prediction?

10. Are there more odd or even numbers? Design a table or graph to record your data in two ways: By row Accumulative Challenge! What is the ratio of even to odd numbers after 3, 7,15 rows?

11. Find your own patterns! Colour multiples of nine What do you see? Try multiples of other numbers are there repeating patterns?

12. More information http://www.mathsisfun.com/pascals-triangle.html