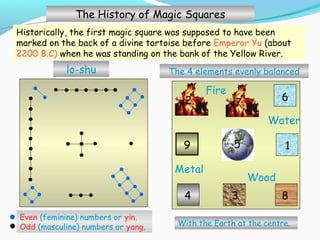
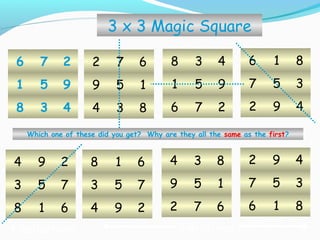
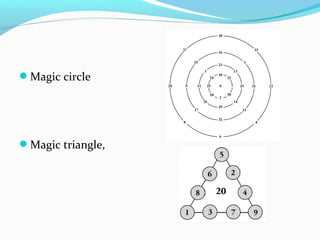
Magic squares are grids of numbers arranged such that the sums of each row, column and diagonal are equal. Historically, the first magic square appeared on the back of a divine tortoise in ancient China. Magic squares have been used for protection, fortune telling and medicine. There are a finite number of unique magic squares depending on size, with more complex types including panmagic, compact, and associative magic squares. Magic squares have applications in mathematics, physics, puzzles and more.

1. By
Dr. Alaa Hussein Lafta

2. What Are Magic Squares?

3. There is no 2x2 magic square
A B
C D

4. The History of Magic Squares
Historically, the first magic square was supposed to have been
marked on the back of a divine tortoise before Emperor Yu (about
2200 B.C) when he was standing on the bank of the Yellow River.
Even (feminine) numbers or yin.
Odd (masculine) numbers or yang.
lo-shu
Water
Fire
Metal
Wood
The 4 elements evenly balanced
With the Earth at the centre.
62
1
834
9 5
7

5. 2008

6. 1:3:5:817
17282817

7. 62
1
8
34
9 5
7

8. In the Middle Ages magic squares were believed to give
protection against the plague!
In the 16th
Century, the Italian mathematician, Cardan,
made an extensive study of the properties of magic squares
and in the following century they were extensively studied
by several leading Japanese mathematicians.
During this century they have been used as amulets in
India, as well as been found in oriental fortune bowls and
medicine cups.
Even today they are widespread in Tibet, (appearing in the
“Wheel of Life) and in other countries such as Malaysia,
that have close connections with China and India.

11. 15
Magic Squares
A 3 x 3 magic Square
Put the numbers 1 to 9 into the square so that all rows,
columns and diagonals add to the magic number.
1
2 3
6 5
4
7
8
9
51 9
2
8
6
43
7

12. 438
951
276 2 7 6
9 5 1
4 3 8
8 3 4
1 5 9
6 7 2
6 1 8
7 5 3
2 9 4
4 9 2
3 5 7
8 1 6
8 1 6
3 5 7
4 9 2
4 3 8
9 5 1
2 7 6
2 9 4
7 5 3
6 1 8
3 x 3 Magic Square
Which one of these did you get? Why are they all the same as the first?
3 Rotations4 Reflections

13. The operations via Magic Squares
• MS + a=MS
• MS * a = MS
• (MS*a)+b =MS
• (MS+a)*b =MS

14. How many magic squares are there?
The nxn magic square Available number
1x1 1
2x2 0
3x3 1
4x4 880
5x5 275 305 224
6x6 1.775399 *10^19
7x7 3.79809*10^34
8x8 5.2225*10^54
9x9 7.8448*10^79
10x10 2.4149*10^110

15. Geometric Types of magic squares
Magic rectangle,
Magic cube,

16. Magic circle
Magic triangle,

17. Magic star
Magic hexagon

18. Different Types of magic squares
Hetero square
Anti-magic square
Semi-magic square
PanMagic (Pandiagonal magic) square
Compact magic square
Complete magic square
Most perfect magic square
Associative (Regular, Symmetric) magic square
Ultra magic square
Alpha Magic square

19. Different Types of magic squares
Magic square of polygonal numbers
(Triangular,Square, Pentagonal, . . . )
Magic square of primes and prime squares
Multi magic square (Bi magic, Tri magic, . . . )
Multiplication magic square
Addition multiplication (Add-mult) magic square
Distributive magic square
Reversible magic square
Palindrome magic square
Domino magic square

21. The magic squares useage
Number theory,
Matrix theory
Graph theory
Matrix models of lie algebras
Cipher
Sudoku
Puzzels
Music nota

22. The magic squares useage
Physical applications as:
From coupled oscillators
Electric quadrupoles
center of mass
Create System of particles and springs
Oscillatory motion of atoms
water retention on square systems

23. Future seminars
The 4x4 magic squares and its properties
Ramanojan Magic Squares
Pandiagonal Magic squares
Even & odd nxn magic squares
Semi magic squares with square numbers.

24. Thank all of You