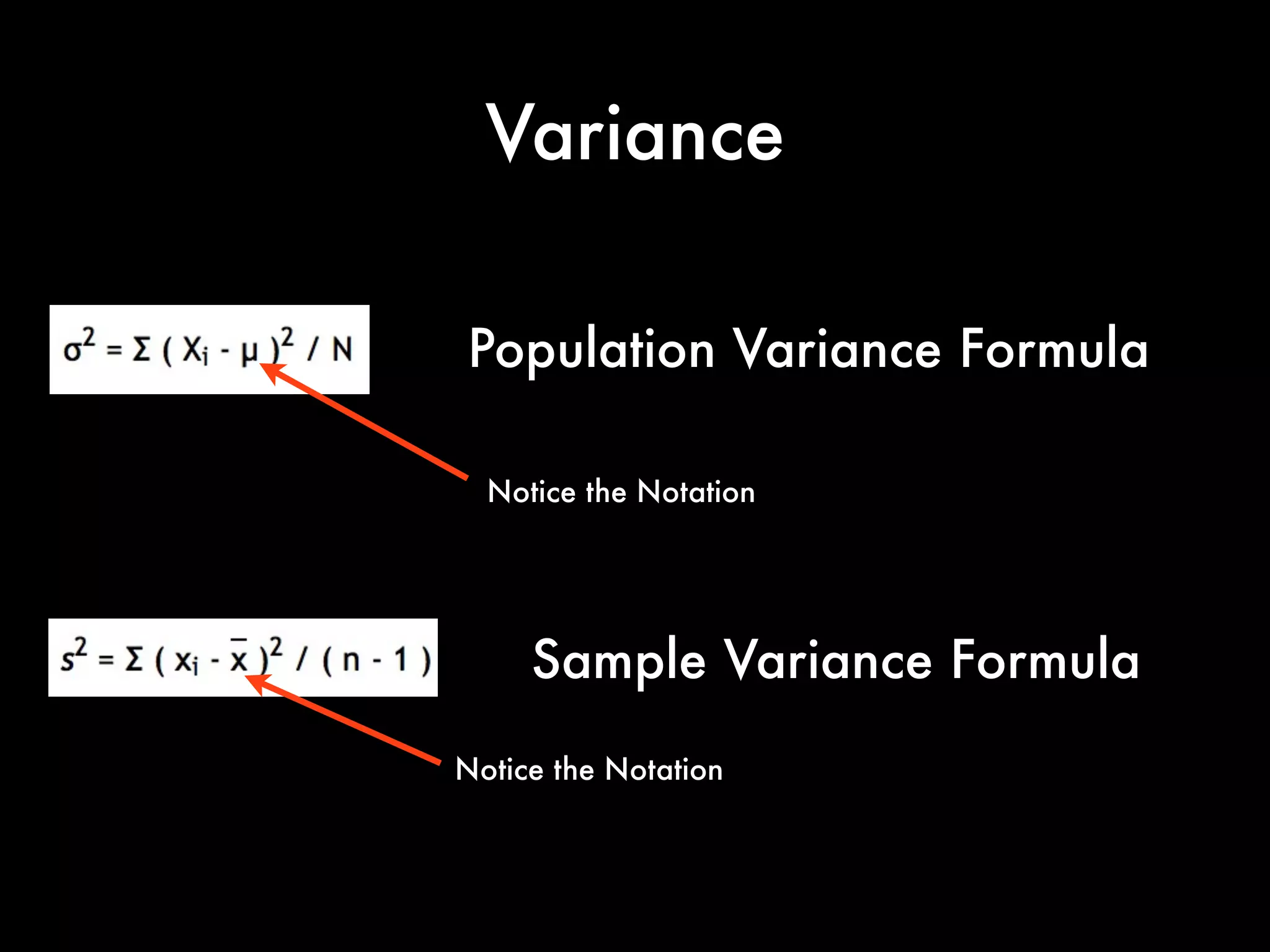
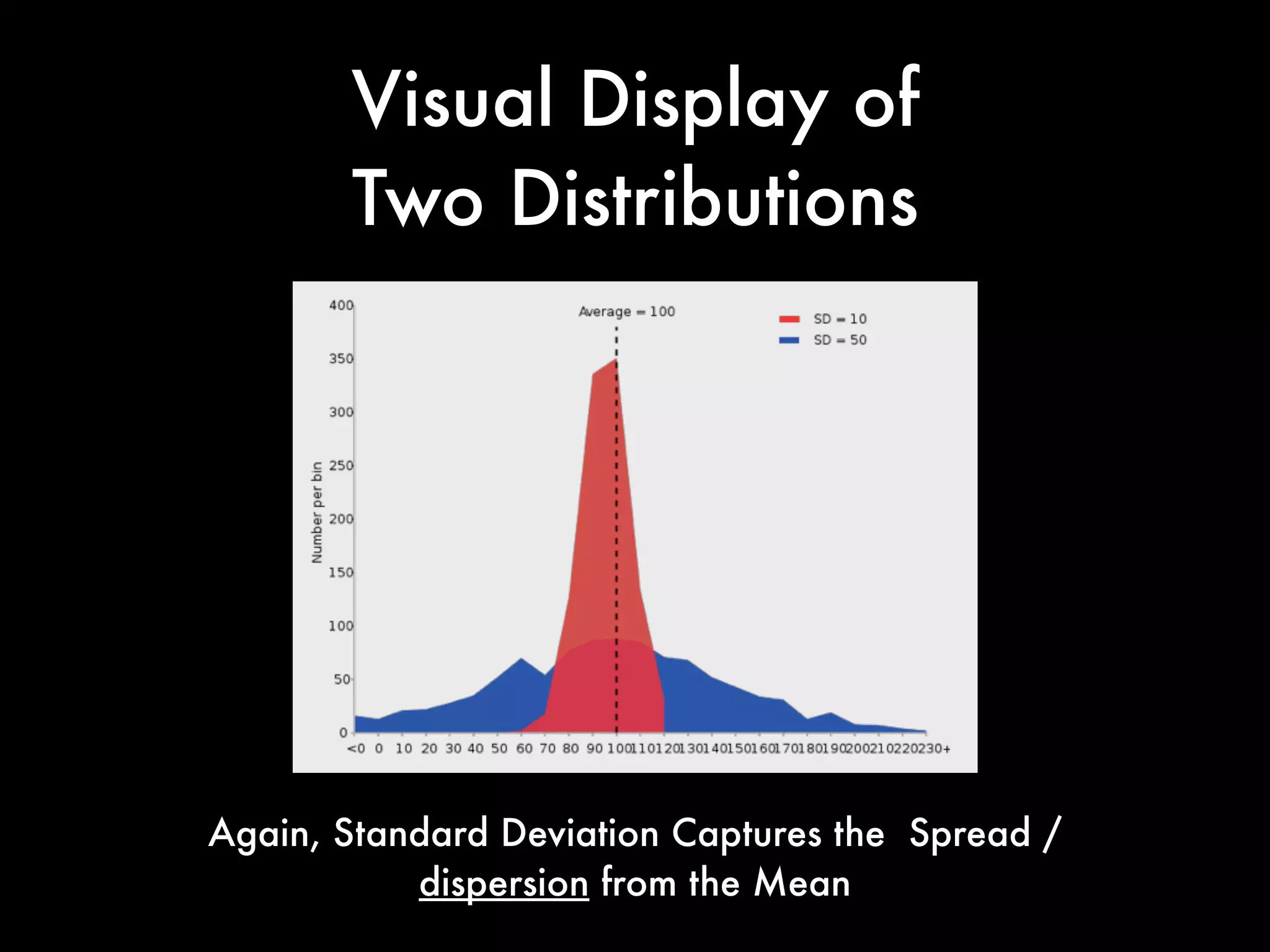
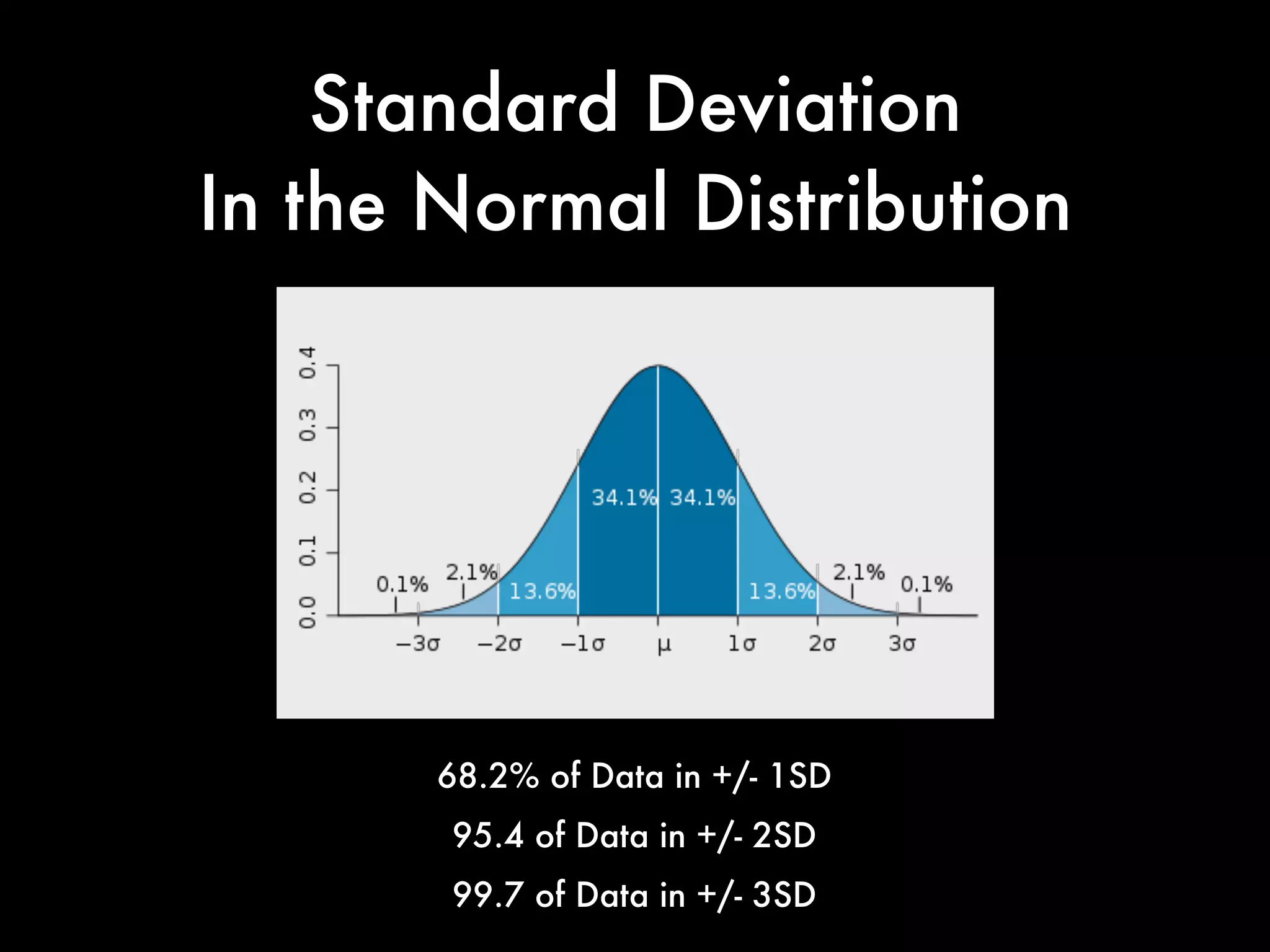
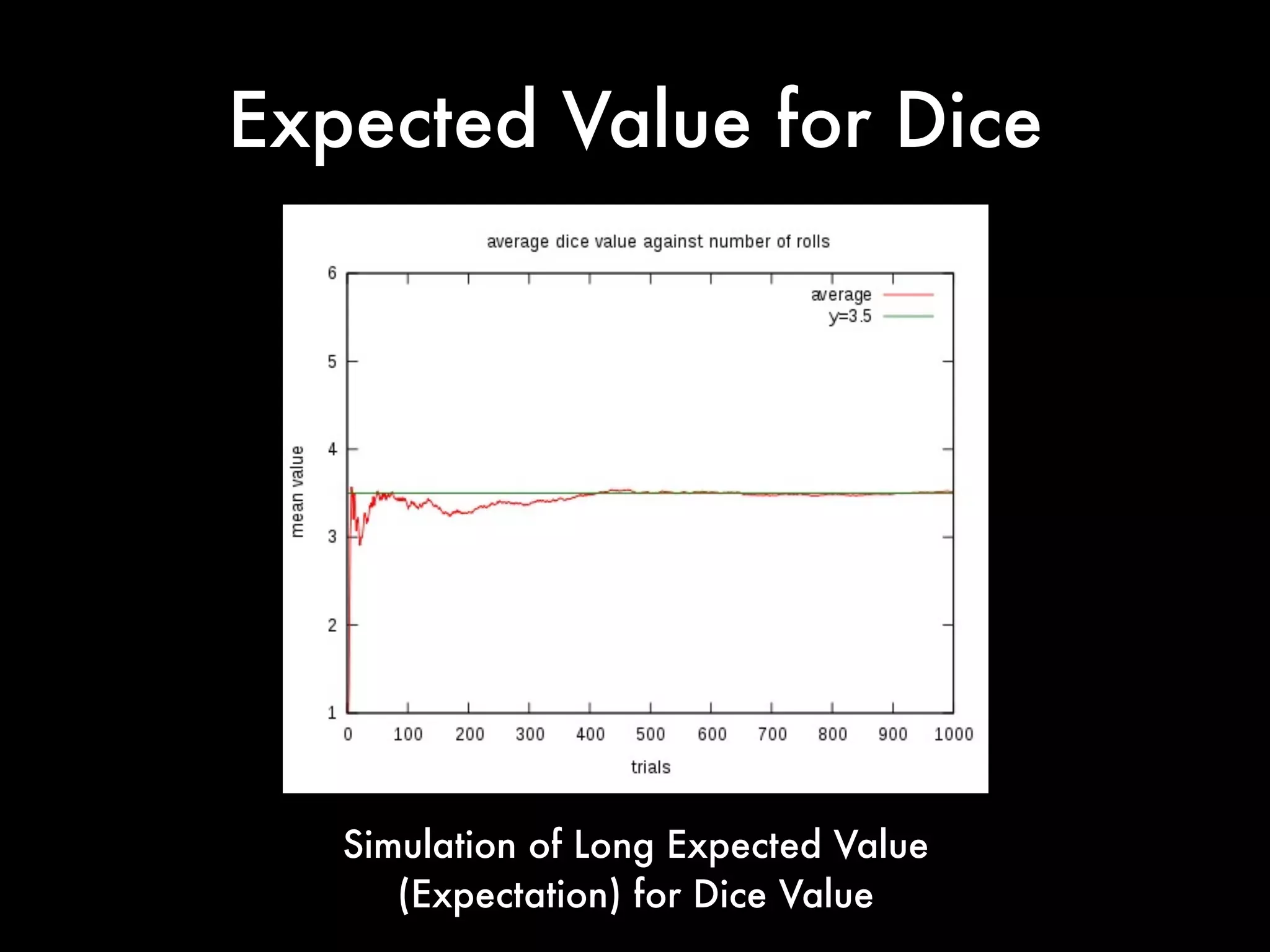
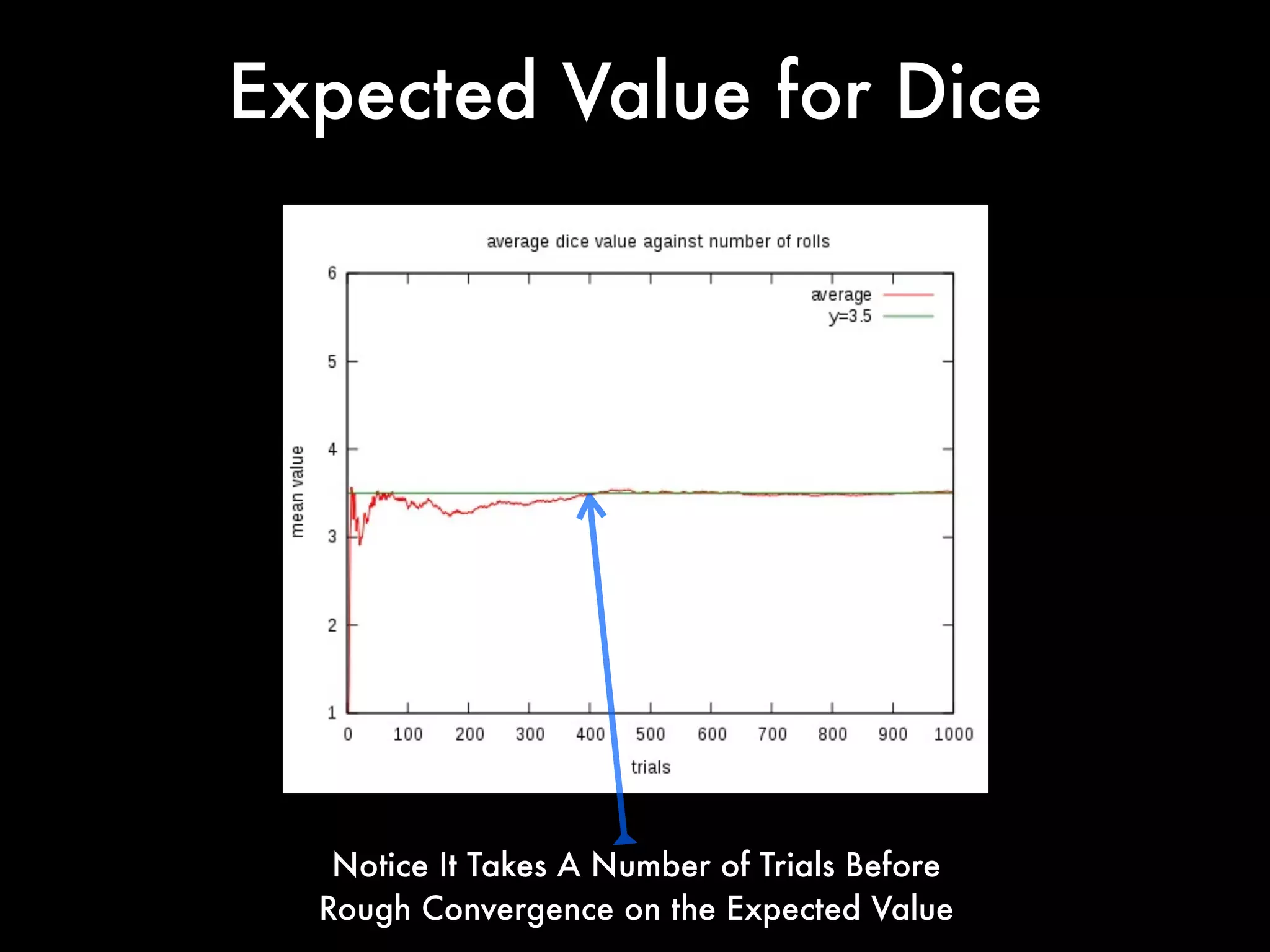
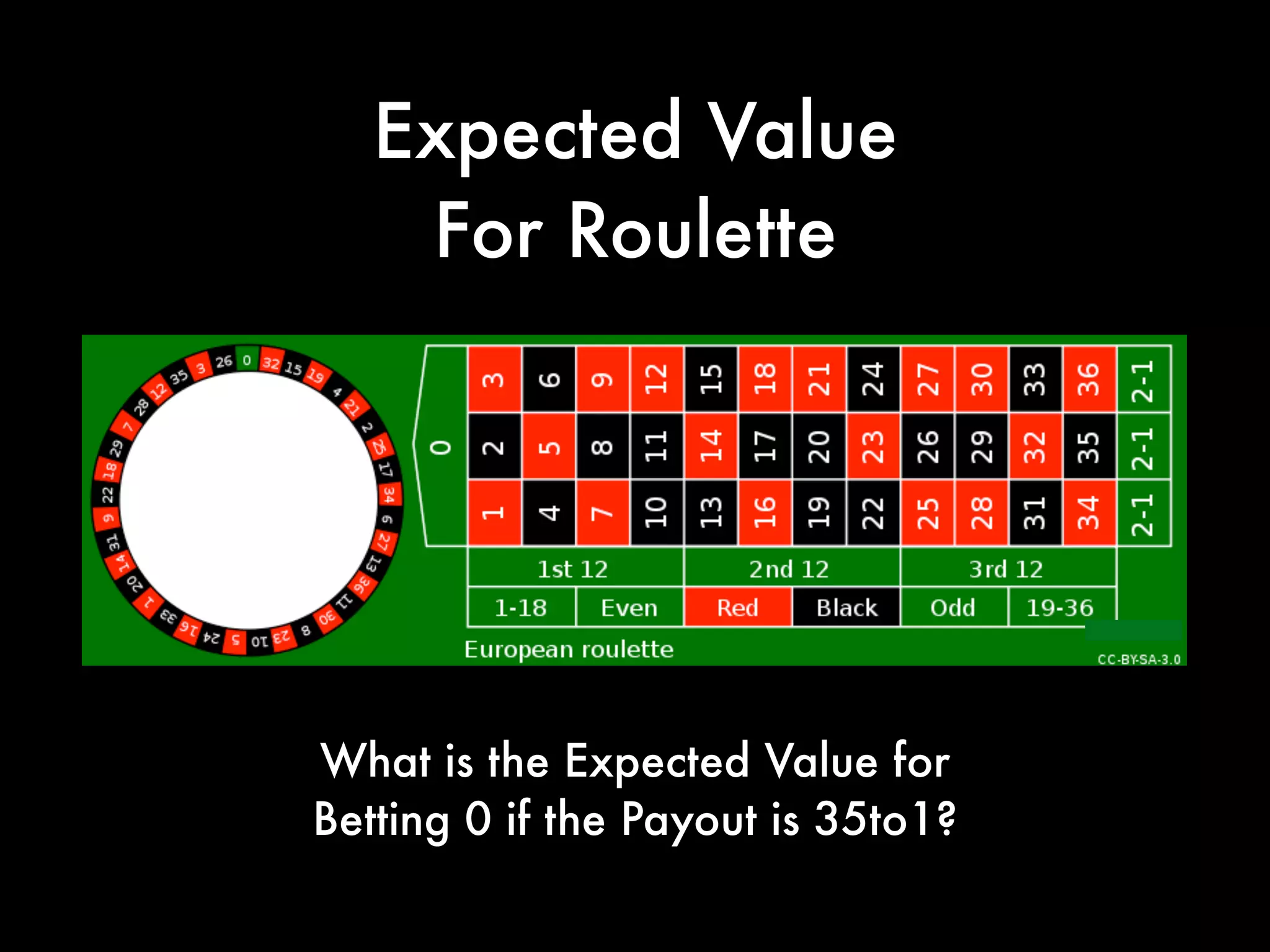
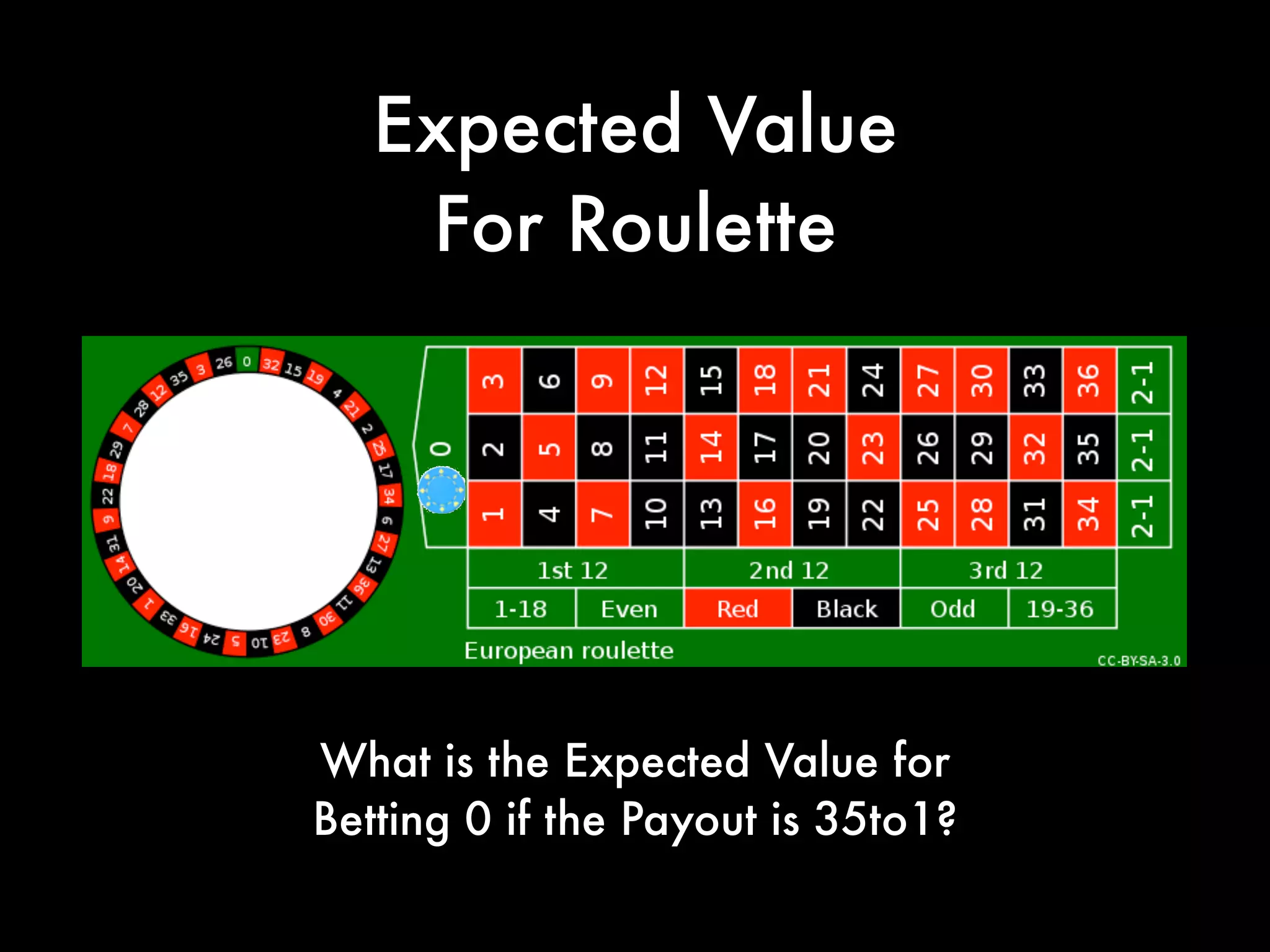
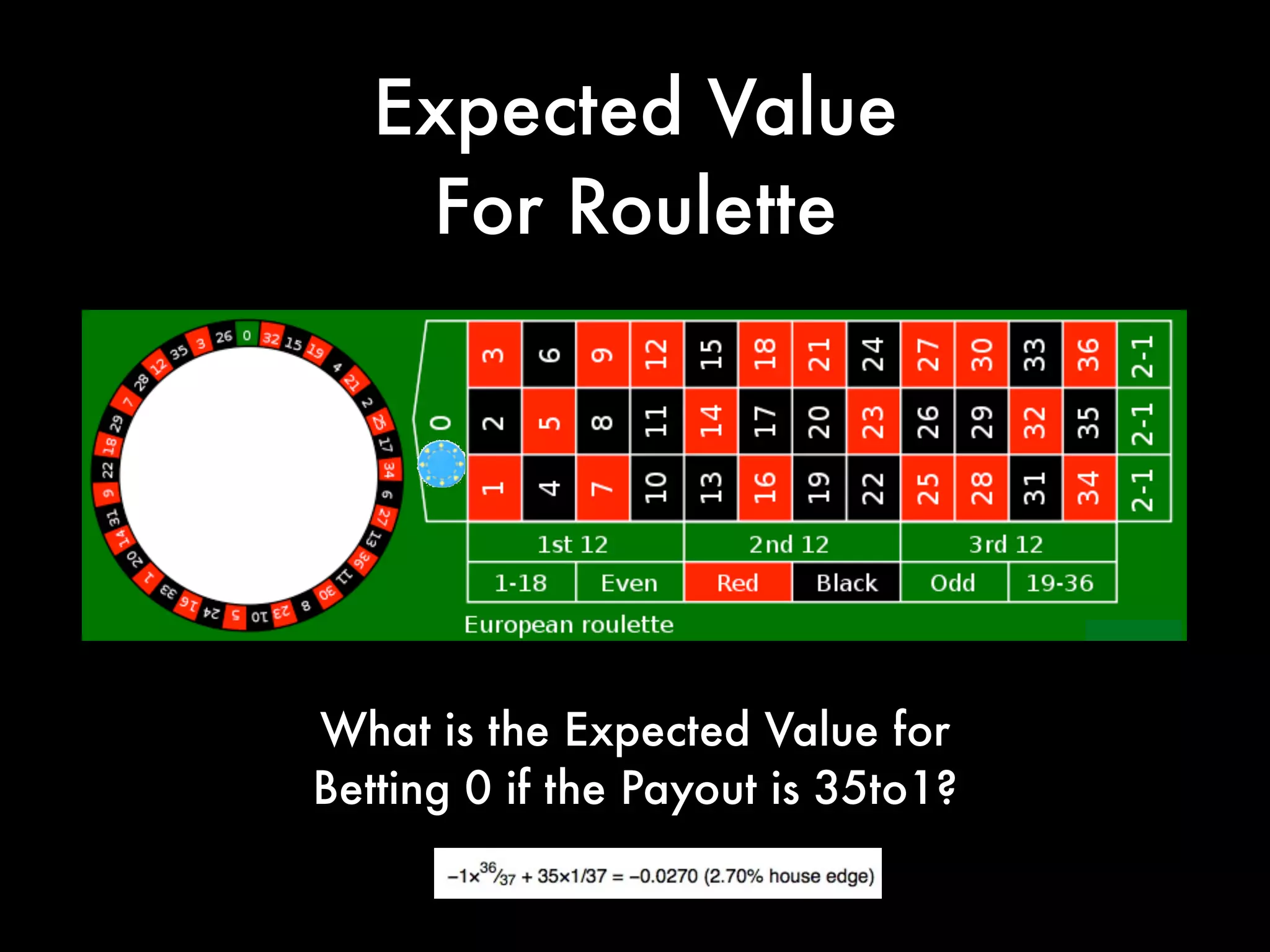
This document covers concepts in statistics relevant for lawyers, focusing on sample statistics versus population parameters, variance, and standard deviation. It includes step-by-step calculations for determining variance and standard deviation using specific data sets, illustrating the impact of these measures on data interpretation. Furthermore, it explains the expected value and its significance in probability and decision-making, particularly in contexts like gaming and betting.

1. Quantitative
Methods
for
Lawyers
Probability &
Basic Statistics (Part 2)
Class #7
@ computational
computationallegalstudies.com
professor daniel martin katz danielmartinkatz.com
lexpredict.com slideshare.net/DanielKatz

2. Quick Word:
Sample Statistics v.
Population Parameters
If it is a variable whose measurement is derived
from a sample, it is a sample statistic.
If it is a variable whose measurement is derived
from a population, it is a population parameter.

3. Last Time We Saw “X Bar”
Technically this is the Notation for a Sample Mean
But I wanted to wait to Discuss this until now ...
Quick Word:
Sample Statistics v.
Population Parameters

4. Variance
Population Variance Formula
Sample Variance Formula

5. Variance
Mean is the First Moment of a Distribution
Variance is the Second Moment of a Distribution

6. Variance
Population Variance Formula
Sample Variance Formula
Notice the Notation
Notice the Notation

7. Variance
(1) Calculate the mean
(2) Calculate the difference between each number
and its mean
(3) Calculate the square of each difference in step #2
(4) Calculate the sum of all the squares in step #3
(5) Take the Sum in Step #4 and
Divide By Either Sample or Population Variance Denominator

8. Variance
(1) Calculate the mean
(6+ 9+ 8 + 9 + 2)/5 = 34/5 = 6.8
Using These Numbers:
6, 9, 8, 9, 2

9. Variance
2) Calculate the difference between each number and its
mean:
(6 - 6.8), (9 - 6.8), (8 - 6.8), (9 - 6.8), (2 - 6.8) =
-0.8, 2.2, 1.2, 2.2, -4.8
Using These Numbers:
6, 9, 8, 9, 2

10. Variance
Using These Numbers:
6, 9, 8, 9, 2
(3) Calculate the square of each difference in step #2
(-0.8)*(-0.8), (2.2)*(2.2), (1.2)*(1.2), (2.2)*(2.2), (-4.8)*(-4.8) =
0.64, 4.84, 1.44, 4.84, 23.04

11. Variance
(4) Calculate the sum of all the squares in step #3
0.64 + 4.84 + 1.44 + 4.84 + 23.04 = 34.8
Using These Numbers:
6, 9, 8, 9, 2

12. Variance
(5) Take the Sum in Step #4 and
Divide By Either Sample or Population Variance Denominator
Assume this is a Sample and thus the Formula is sample size - 1
Variance = 34.8/(5-1) = 34.8/4 = 8.7
Note: If Population Var = 6.96
Using These Numbers:
6, 9, 8, 9, 2

13. Variance
Please Get in Small Groups and
Calculate the Sample Variance By Hand
for the Following Data Set:
3, 8, 12, 22, 34, 45, 48, 58

14. Variance
(1) Calculate the mean
(3 + 8 + 12 + 22 + 34+ 45 +48 + 58) /8 =
230/8 =
28.75
Using These Numbers:
3, 8, 12, 22, 34, 45, 48, 58

15. Variance
(2) Calculate the difference between each number and its m
(3 - 28.75), (8 - 28.75), (12 - 28.75), (22 - 28.75), (34 - 28.75) ,
(45 - 28.75) (48 - 28.75) (58 - 28.75) =
-25.75, 20.75, -16.75, -6.75, +5.25
+16.25, +19.25 +29.25
Using These Numbers:
3, 8, 12, 22, 34, 45, 48, 58

16. Variance
(3) Calculate the square of each difference in step #2
(-25.75)2
, (-20.75)2
, (-16.75)2
, (-6.75)2
, (5.25) 2
(16.25) 2
, (19.25)2
, (29.25) 2
Using These Numbers:
3, 8, 12, 22, 34, 45, 48, 58
663.0625, 430.5625 , 280.5625, 45.5625, 27.5625,
264.0625, 370.5625 , 855.5625

17. Variance
(4) Calculate the sum of all the squares in step #3
663.0625 +430.5625 + 280.5625 + 45.5625 + 27.5625+
264.0625 + 370.5625 + 855.5625 =
2937.5
Using These Numbers:
3, 8, 12, 22, 34, 45, 48, 58

18. Variance
(5) Take the Sum in Step #4 and
Divide By Either Sample or Population Variance Denominator
Assume this is a Sample and thus the Formula is sample size - 1
Variance = 2937.5/(8-1) = 2937.5/(8-1) = 419.64
Using These Numbers:
3, 8, 12, 22, 34, 45, 48, 58

19. Variance
Please Get in Small Groups and
Calculate the Sample Variance By Hand
for the Following Data Set:
3, 8, 12, 22, 34, 45, 48, 58
~419.6

20. Standard Deviation
Again, we have the
Sample v. Population
Notation Distinction

21. Standard Deviation
Standard deviation is a widely used measure of
variability or diversity used in statistics and probability
theory.
It shows how much variation or "dispersion" exists from
the average (mean, or expected value).
A low standard deviation indicates that the data points
tend to be very close to the mean, whereas high
standard deviation indicates that the data points are
spread out over a large range of values.

22. Visual Display of
Two Distributions
Again, Standard Deviation Captures the Spread /
dispersion from the Mean

23. Standard Deviation
Standard Deviation is the Square Root
of the Variance ...
Sample
Variance
Formula
Sample
Standard
deviation
Formula

24. Standard Deviation
Using These Numbers:
3, 8, 12, 22, 34, 45, 48, 58
~419.64
And This Formula:
=
We Obtained This Result

25. Standard Deviation
(Sample Standard Deviation Formula)
So We Just Need to Take the Root of This
Result As Follows:
419.64
Voilà - Our Result
20.48
(Insert Our Prior Result)

26. Standard Deviation
Standard deviation is only used to measure spread or
dispersion around the mean of a data set.
Standard deviation is never negative.
Standard deviation is sensitive to outliers. A single outlier
can raise the standard deviation and in turn, distort the
picture of spread.
For data with approximately the same mean, the greater the
spread, the greater the standard deviation.
Note: If all values of a data set are the same, the
standard deviation is zero (because each value is
equal to the mean).

27. Standard Deviation
In the Normal Distribution
68.2% of Data in +/- 1SD
95.4 of Data in +/- 2SD
99.7 of Data in +/- 3SD

28. Expected Value

29. Expected Value
the expected value (or expectation, or
mathematical expectation, or mean, or the first
moment) of a random variable is the weighted
average of all possible values that this random
variable can take on.
The weights used in computing this average
correspond to the probabilities.

30. Expected Value
The expected value may be intuitively understood
by the law of large numbers:
the expected value, when it exists, is almost surely
the limit of the sample mean as sample size grows
to infinity.

31. Expected Value
It can be interpreted as the long-run average of
the results of many independent repetitions of an
experiment
(e.g. a dice roll, Coin Flip, etc).
Note: the value may not be expected in the ordinary sense—the "expected
value" itself may be unlikely or even impossible (such as having 2.5
children), just like the sample mean.

32. Why Is Expected
Value Useful?
Do NOT PLAY GAMES WITH A
NEGATIVE EXPECTED VALUE AS YOU WILL
EVENTUALLY LOSE AS
N > +∞-

33. Expected Value for Dice
What is the Expected # of Pips?
What is xi in this Case?
What is pi in this Case?

34. Expected Value for Dice
What is the Expected # of Pips?
What is xi in this Case?
What is pi in this Case?
Each Pip

35. Expected Value for Dice
What is the Expected # of Pips?
What is xi in this Case?
What is pi in this Case?
Each Pip
Prob of Each Pip

36. Expected Value for Dice
What is the Expected # of Pips?
What is xi in this Case?
What is pi in this Case?
Each Pip
Prob of Each Pip

37. Expected Value for Dice
Simulation of Long Expected Value
(Expectation) for Dice Value

38. Expected Value for Dice
Notice It Takes A Number of Trials Before
Rough Convergence on the Expected Value

39. Expected Value
For Roulette

40. Expected Value
For Roulette
What is the Expected Value for
Betting 0 if the Payout is 35to1?

41. Work Through this Problem
Out Your Own

42. Expected Value
For Roulette
What is the Expected Value for
Betting 0 if the Payout is 35to1?

43. Now Try This Problem

44. Expected Value
For Roulette
What is the Expected Value for
Betting 0 if the Payout is 35to1?

45. Expected Value
For Roulette
What is the Expected Value for
Betting 0 if the Payout is 35to1?

46. Expected Value
For Roulette
What is the Expected Value for
Betting 0 if the Payout is 35to1?

47. Daniel Martin Katz
@ computational
computationallegalstudies.com
lexpredict.com
danielmartinkatz.com
illinois tech - chicago kent college of law@