The document describes the disadvantages of software for multi-parameter visualization. It identifies three main disadvantages: (1) a large number of contour diagrams must be drawn with some parameters fixed, (2) the accuracy of the analysis depends on the discretization of the fixed parameters, and (3) the contour diagrams are not arranged according to their values. It provides an example using four parameters (X1, X2, X3, X4) to illustrate these disadvantages.

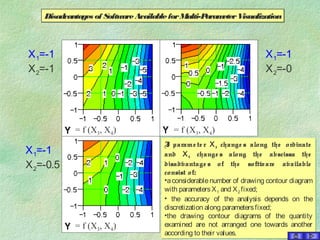
1. Disadvantages of SoftwareAvailableforMulti-ParameterVisualizationDisadvantages of SoftwareAvailableforMulti-ParameterVisualization
If parame te r Х3 change s along the ordinate
and Х4 change s along the abscissa the
disadvantage s of the software available
consist of:
•aconsiderablenumber of drawing contour diagram
with parametersХ1 and Х2 fixed;
• the accuracy of the analysis depends on the
discretization along parametersfixed;
•the drawing contour diagrams of the quantity
examined are not arranged one towards another
according to their values.
If parame te r Х3 change s along the ordinate
and Х4 change s along the abscissa the
disadvantage s of the software available
consist of:
•aconsiderablenumber of drawing contour diagram
with parametersХ1 and Х2 fixed;
• the accuracy of the analysis depends on the
discretization along parametersfixed;
•the drawing contour diagrams of the quantity
examined are not arranged one towards another
according to their values.
X1=-1
X2=-1
X1=-1
X2=-0.5
X1=-1
X2=-0
= f (X3, X4) = f (X3, X4)
= f (X3, X4)

2. To prove the state me nt pre se nte d above the following
e xample can be give n. If discre tization is chose n along Х1
with points [-1, -0.5, 0, 0.5, 1] with X2 =-1 fixe d and it is
acce pte d that Х3 change s along the ordinate and Х4
change s along the abscissa the n:
• a considerable number of diagram patterns can be watched with
parameter Х2 fixed;
• theaccuracy of theanalysisdependson thevery discretization of
theparameter fixed;
• the contour diagrams of quantity Y examined are not arranged
onetowardsanother according to their values.
To prove the state me nt pre se nte d above the following
e xample can be give n. If discre tization is chose n along Х1
with points [-1, -0.5, 0, 0.5, 1] with X2 =-1 fixe d and it is
acce pte d that Х3 change s along the ordinate and Х4
change s along the abscissa the n:
• a considerable number of diagram patterns can be watched with
parameter Х2 fixed;
• theaccuracy of theanalysisdependson thevery discretization of
theparameter fixed;
• the contour diagrams of quantity Y examined are not arranged
onetowardsanother according to their values.
X1=-1 X1=-0.5 X1=0 X1=0.5 X1=1
X2=-1
Disadvantages of SoftwareAvailableforMulti-ParameterVisualizationDisadvantages of SoftwareAvailableforMulti-ParameterVisualization
(x1, x2, x3, x4)=a1+a2.x1+a3.x2+a4.x3+a5.x4+a6.x1
2
+a7.x1.x2+a8.x1.x3+a9.x1.x4+
+a10.x2
2
+a11.x2.x3+a12.x2.x4+a13.x3
2
+a14.x3.x4+a15.x4
2
a1= 0.4325 a6=-1.196 a11=
2.15432
a2=-0.008248 a7=-0.259 a12=
1.01693
a3=-0.228915 a8= 2.9977 a13=-
1.95535
a4= 0.033695 a9= 0.15847 a14=-
0.944752

3. It is ne ce ssary to e xamine 25
contour diagrams like the one s pointe d to
the le ft whe re Х1 and Х2 vary in orde r to
orie nt the De cision-Make r in the
discre tization give n along Х1, Х2, Х3 and Х4
with a se t of discre te points [-1, -0.5, 0, 0.5,
1].
In that case the re is only one
proble m and it conce rns the contour
diagrams which are not arrange d one
towards anothe r.
It is ne ce ssary to e xamine 25
contour diagrams like the one s pointe d to
the le ft whe re Х1 and Х2 vary in orde r to
orie nt the De cision-Make r in the
discre tization give n along Х1, Х2, Х3 and Х4
with a se t of discre te points [-1, -0.5, 0, 0.5,
1].
In that case the re is only one
proble m and it conce rns the contour
diagrams which are not arrange d one
towards anothe r.
Disadvantages of SoftwareAvailableforMulti-ParameterVisualizationDisadvantages of SoftwareAvailableforMulti-ParameterVisualization
(x1, x2, x3, x4)=a1+a2.x1+a3.x2+a4.x3+a5.x4+a6.x1
2
+a7.x1.x2+a8.x1.x3+a9.x1.x4+
+a10.x2
2
+a11.x2.x3+a12.x2.x4+a13.x3
2
+a14.x3.x4+a15.x4
2
a1= 0.4325 a6=-1.196 a11=
2.15432
a2=-0.008248 a7=-0.259 a12=
1.01693
a3=-0.228915 a8= 2.9977 a13=-
1.95535
a4= 0.033695 a9= 0.15847 a14=-

4. All thre e -surface diagrams shown above pre se nt the contour diagram information se e n
unde r diffe re nt angle s. The conne ction be twe e n the value of the quantity e xamine d and
the addre ss of the control parame te rs is difficult and not e xact to be indicate d (by the
thre e -surface diagrams).
All thre e -surface diagrams shown above pre se nt the contour diagram information se e n
unde r diffe re nt angle s. The conne ction be twe e n the value of the quantity e xamine d and
the addre ss of the control parame te rs is difficult and not e xact to be indicate d (by the
thre e -surface diagrams).
MADMML®
Principle of Multi-Parame te r VisualizationMADMML®
Principle of Multi-Parame te r Visualization
MADMML®
use s its modification of a contour diagram be cause its thre e -me asure me nt
visualization is inde pe nde nt of the diagram rotation along its ve rtical axis.
MADMML®
use s its modification of a contour diagram be cause its thre e -me asure me nt
visualization is inde pe nde nt of the diagram rotation along its ve rtical axis.

5. STEPISTEPI
-Re pre se ntation of the are a whe re multi-parame te r visualization will be carrie d out
STEPISTEPI
-Re pre se ntation of the are a whe re multi-parame te r visualization will be carrie d out
MADMML®
Principle of Multi-Parame te r VisualizationMADMML®
Principle of Multi-Parame te r Visualization

6. STEPIISTEPII
- discre tisation of the fie ld in re lation to parame te r X1 with give n limitations and a ste p of change
STEPIISTEPII
- discre tisation of the fie ld in re lation to parame te r X1 with give n limitations and a ste p of change
MADMML®
Principle of Multi-Parame te r VisualizationMADMML®
Principle of Multi-Parame te r Visualization
X1

7. STEPIIISTEPIII
- discre tisation of the fie ld in re lation to parame te r X2 with give n limitations and a ste p of
change as we ll as formation of forming an instrume nt to ke e p up with the change s of X1
and X2.
STEPIIISTEPIII
- discre tisation of the fie ld in re lation to parame te r X2 with give n limitations and a ste p of
change as we ll as formation of forming an instrume nt to ke e p up with the change s of X1
and X2.
MADMML®
Principle of Multi-Parame te r VisualizationMADMML®
Principle of Multi-Parame te r Visualization
X1
X2

8. STEPIVSTEPIV
- discre tisation of the fie ld in re lation to parame te r X3 with give n limitations and a ste p of change
STEPIVSTEPIV
- discre tisation of the fie ld in re lation to parame te r X3 with give n limitations and a ste p of change
MADMML®
Principle of Multi-Parame te r VisualizationMADMML®
Principle of Multi-Parame te r Visualization
X1
X2
X3

9. STEPVSTEPV
-discre tisation of the fie ld in re lation to parame te r X4 with give n limitations and a ste p of
change as we ll as input of a global addre ss de te rmining syste m according to all variable s
ne ce ssary for visualization of the parame te r mode l.
STEPVSTEPV
-discre tisation of the fie ld in re lation to parame te r X4 with give n limitations and a ste p of
change as we ll as input of a global addre ss de te rmining syste m according to all variable s
ne ce ssary for visualization of the parame te r mode l.
MADMML®
Principle of Multi-Parame te r VisualizationMADMML®
Principle of Multi-Parame te r Visualization
X1
X2
X3
X4

10. The proce ss of multi-factor analysis is re alize d through MADMMLMADMMLinstrume nts in the
space s of parame te rs. With the indicate d discre tisation, 94
=6561conbination among the
indicate d four variable s are simultane ously analyze d .
The proce ss of multi-factor analysis is re alize d through MADMMLMADMMLinstrume nts in the
space s of parame te rs. With the indicate d discre tisation, 94
=6561conbination among the
indicate d four variable s are simultane ously analyze d .
MADMML®
Principle of Multi-Parame te r VisualizationMADMML®
Principle of Multi-Parame te r Visualization
X1
X2
X3
X4
MADMMLMADMMLinstrume nts of parame te r
space analysis
MADMMLMADMMLinstrume nts of parame te r
space analysis

11. The approach so de fine d is dynamicallyThe approach so de fine d is dynamically
illustrate d by the Compass De vice of MADMMLillustrate d by the Compass De vice of MADMML
The movable limits possibilitie s with theThe movable limits possibilitie s with the
analysis only of one of the crite ria is re ve ale d by aanalysis only of one of the crite ria is re ve ale d by a
numbe r of slide s following be low:numbe r of slide s following be low:

12. Y[1] 0 .. 90 %
Y[2] 90 .. 100 %
Y(x1, x2, x3, x4)=a1+a2.x1+a3.x2+a4.x3+a5.x4+a6.x1
2
+a7.x1.x2+a8.x1.x3+a9.x1.x4+
+a10.x2
2
+a11.x2.x3+a12.x2.x4+a13.x3
2
+a14.x3.x4+a15.x4
2
a1= 0.4325 a6=-1.196 a11= 2.15432
a2=-0.008248 a7=-0.259 a12= 1.01693
a3=-0.228915 a8= 2.9977 a13=-
1.95535
a4= 0.033695 a9= 0.15847 a14=-
0.944752
a5= 0.003165 a10= 0.61596 a15=
Single -crite ria analysis with movable
limits
The method helps in
determining the direction of
searching. The zones colored
in green show areas where the
values of the quantity
examined areover 90%

13. Y[1] between 0 .. 96 %
Y[2] between 96 .. 97 %
Y[3] between 97 .. 98 %
Y[4] between 98 .. 99 %
Y[5] between 99 .. 100 %
Single -crite ria analysis with movable
limits
Localizing the area and
determining certain solutions.
Representing the solutions by
appropriatecontour diagrams

14. Y[1] 0 .. 60 %
Y[2] 60 .. 70 %
Y[3] 70 .. 80 %
Y[4] 80 .. 90 %
Y[5] 90 .. 100 %
Y[1] 0 .. 80 %
Y[2] 80 .. 85 %
Y[3] 85 .. 90 %
Y[4] 90 .. 95 %
Y[5] 95 .. 100 %
Y[1] 0 .. 80 %
Y[2] 85 .. 90 %
Y[3] 90 .. 95 %
Y[4] 95 .. 99 %
Y[5] 99 .. 100 %
Y[1] 0 .. 92 %
Y[2] 92 .. 94 %
Y[3] 94 .. 96 %
Y[4] 96 .. 98 %
Y[5] 98 .. 100 %
Single -crite ria analysis with movable
limits
Determining parameters characterized by
near values in the space examined with the
movement of “cutting” values up towards the
maximum.

15. Y[1] 0 .. 2 %
Y[2] 2 .. 4 %
Y[3] 4 .. 6 %
Y[4] 6 .. 8 %
Y[5] 8 .. 100 %
Y[1] 0 .. 5 %
Y[2] 5 .. 10 %
Y[3] 10 .. 15 %
Y[4] 15 .. 20 %
Y[5] 20 .. 100 %
Y[1] 0 .. 10 %
Y[2] 10 .. 20 %
Y[3] 20 .. 30 %
Y[4] 30 .. 40 %
Y[5] 40 .. 100 %
Y[1] 0 .. 30 %
Y[2] 30 .. 40 %
Y[3] 40 .. 50 %
Y[4] 50 .. 60 %
Y[5] 60 .. 100 %
Single -crite ria analysis with movable
limits
Determining parameters characterized by near
values in the space examined with the
movement of “cutting” values down towards
theminimum.

16. Y[1] 0 .. 80 %
Y[2] 80 .. 81 %
Y[3] 81 .. 100 %
Y(x1, x2, x3, x4)=a1+a2.x1+a3.x2+a4.x3+a5.x4+a6.x1
2
+a7.x1.x2+a8.x1.x3+a9.x1.x4+
+a10.x2
2
+a11.x2.x3+a12.x2.x4+a13.x3
2
+a14.x3.x4+a15.x4
2
a1= 0.4325 a6=-1.196 a11= 2.15432
a2=-0.008248 a7=-0.259 a12= 1.01693
a3=-0.228915 a8= 2.9977 a13=-
1.95535
a4= 0.033695 a9= 0.15847 a14=-
0.944752
a5= 0.003165 a10= 0.61596 a15=
Single -crite ria analysis with movable
limits
Determining the states where the
quality parameter contains an
exactly determined value. The
value of the quantity examined in
all areas colored in green are
within the interval between 80%
and 81%.